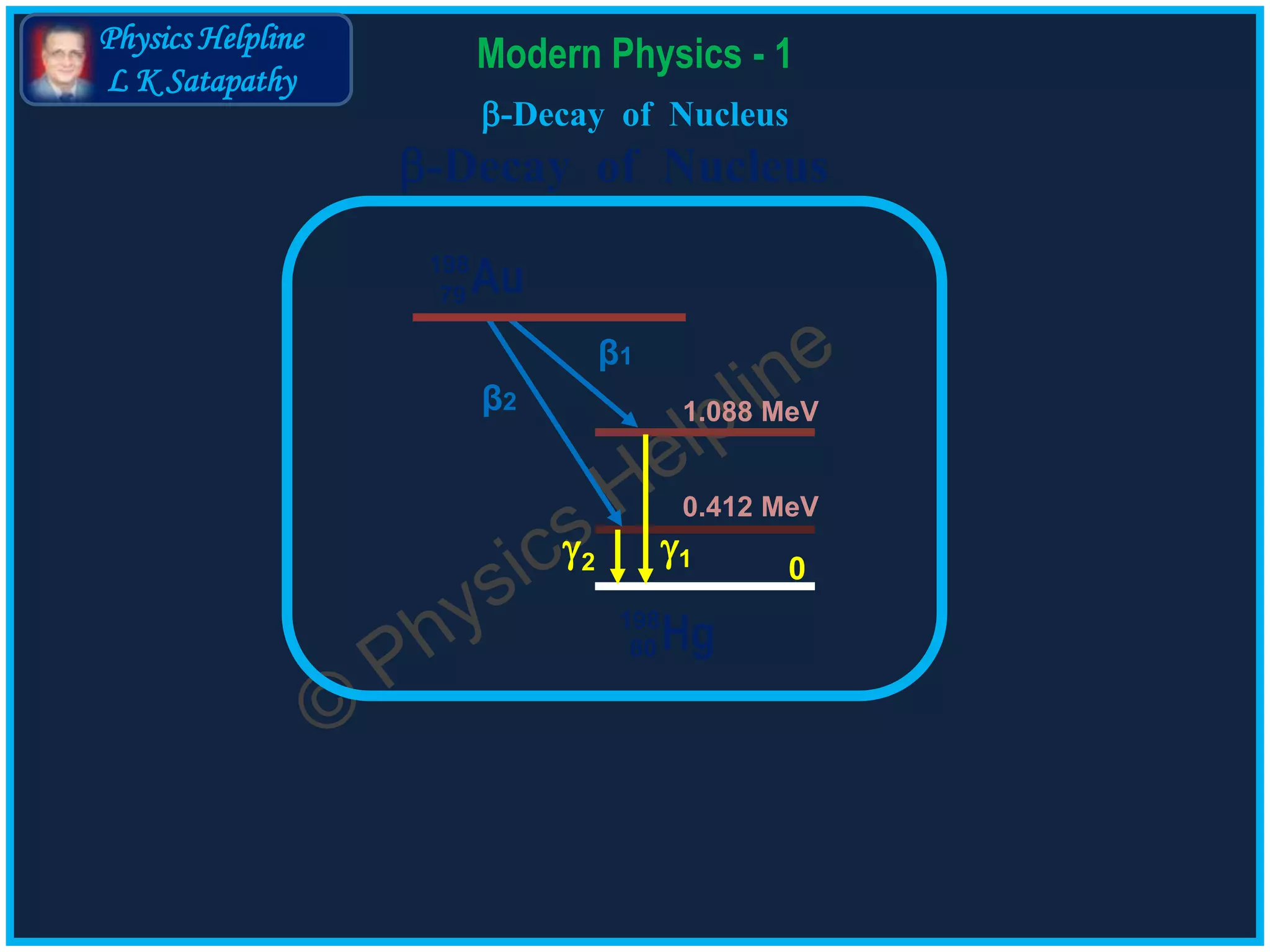
The document discusses the β-decay of gold nuclei into mercury, detailing the emission of γ-rays and the calculation of kinetic energies of emitted β-particles. It includes equations for energy release during β-decay based on mass differences and the associated excitation energies of the resultant nuclei. The maximum possible kinetic energies for two decaying nuclei are calculated as 0.284 MeV and 0.960 MeV, respectively, along with the frequencies of emitted γ-rays.

1. Physics Helpline
L K Satapathy
Modern Physics - 1
-Decay of Nucleus
79
β2
β1
Au198

Hg
1.088 MeV
0.412 MeV
12 0
80
198
-Decay of Nucleus

2. Physics Helpline
L K Satapathy
Modern Physics - 1
-Decay of Nucleus
79
1β
β2
Au198

80 Hg198
1.088 MeV
0.412 MeV
12

Question :
Two gold nuclei undergo β-decay and
convert to mercury in ground state
through different excited states with
subsequent emission of -rays as per the
decay scheme shown in the figure. Find
(a) The maximum possible kinetic
energies of the β - particles
(b) the frequencies of the  - rays.
Given : The atomic masses are
198
79( ) 197.968233m Au u
198
80( ) 197.966760m Hg uand

3. Physics Helpline
L K Satapathy
Modern Physics - 1
-Decay of Nucleus
Concepts
Eqn. for β – decay [electron emission] :  
  1
A A
Z ZX Y
Energy is released when ( Final Mass ) < ( Initial Mass )
Decrease in 1 amu of mass releases 931.5 MeV of energy
Decrease in mass = Initial mass – Final mass ( = ∆m )
 Energy released = ∆m  931.5 MeV
Planck’s constant 
  34
6.625 10 .h J s

4. Physics Helpline
L K Satapathy
Modern Physics - 1
-Decay of Nucleus
 KE of β particle = Energy released – Excitation energy
Here ∆E is to be expressed in JOULE using
Part of the energy released is retained by the product nucleus as excitation
energy and the remaining energy is emitted in the form of a -ray.
A -ray photon is emitted when the product nucleus jumps down from excited
state to ground state.
 Frequency of  - ray is 

 
' .
changeinenergy E
f
Planck s Const h

  13
1 1.6 10MeV J

5. Physics Helpline
L K Satapathy
Modern Physics - 1
-Decay of Nucleus
Initial mass = mass of the decaying nucleus
     198 198
79 80[ ( ) 79 ] [ ( ) 80 ]e e em m Au m m Hg m m
  197.968233 197.966760 0.001473u
 Energy released = 0.001473  931.5 = 1.372 MeV
 198 198
79 80( ) ( )m Au m Hg
For both nuclei , the decrease in mass is the same
Final mass = mass of the product nucleus + mass of -particle
 198
79( ) 79 em Au m
  198
80( ) 80 e em Hg m m

6. Physics Helpline
L K Satapathy
Modern Physics - 1
-Decay of Nucleus
For the 1st nucleus energy released = 1.372 MeV


  
   

13
20
1 34
1.088 1.6 10
2.627 10
6.62
[
5 10
]
E
f Hz Ans
h
 KE of β1 = 1.372 – 1.088 = 0.284 MeV [Ans]
Its excitation energy = 1.088 MeV
When the nucleus jumps down to ground state ,
energy of the emitted -ray = the excitation energy
 Frequency of the emitted -ray is given by

7. Physics Helpline
L K Satapathy
Modern Physics - 1
-Decay of Nucleus
 KE of β2 = 1.372 ─ 0.412 = 0.960 MeV [Ans]


  
   

13
20
2 34
0.412 1.6 10
0.995 10
6.62
[
5 10
]
E
f Hz Ans
h
For the 2nd nucleus also, energy released = 1.372 MeV
Its excitation energy = 0.412 MeV
When the nucleus jumps down to ground state ,
energy of the emitted -ray = the excitation energy
 Frequency of the emitted -ray is given by

8. Physics Helpline
L K Satapathy
For More details:
www.physics-helpline.com
Subscribe our channel:
youtube.com/physics-helpline
Follow us on Facebook and Twitter:
facebook.com/physics-helpline
twitter.com/physics-helpline