Molecular dynamics (MD) is a computer simulation technique used to model physical movements of atoms and molecules over time. MD simulations involve numerically solving classical equations of motion to simulate interactions between atoms at different scales, from molecular to human to planetary. While MD can provide detailed atomic-level insights, it has limitations such as potential issues with numerical integration accuracy at small time steps.

1. 0101011
0000000
1110100
0110001
1
0
Molecular Dynamics
Sparisoma Viridi
Nuclear Physics and Biophysics Research Division
Institut Teknologi Bandung, Bandung 40132, Indonesia
dudung@fi.itb.ac.id
v2011.09.20 FI3102 Computational Physics 1

2. 0101011
0000000
1110100
0110001 Outline
1
• Molecular dynamics
0
• The use of molecular dynamics
• Experiment using simulation
• Molecular scale, human scale, planetoid
• MD algorithm and example
• Is MD so perfect?
v2011.09.20 FI3102 Computational Physics 2

3. 0101011
0000000
1110100
0110001 Molecular dynamics
1
• Molecular dynamics (MD) is a computer
0
simulation of physical movements of
atoms and molecules (Wikipedia, 2011)
• MD simulation consists of the numerical,
step-by-step, solution of classical equation
of motion (Allen, 2004)
v2011.09.20 FI3102 Computational Physics 3

4. 0101011
0000000
1110100
0110001 Molecular dynamics (cont.)
1
• It is a computer simulation technique
0
where the time evolution of a set of
interacting atoms is followed by integrating
their equations of motion (Ercolessi, 1997)
• MD simulations can provide the ultimate
detail concerning individual motions as a
function of time (Karplus and McCammon,
2002)
v2011.09.20 FI3102 Computational Physics 4

5. 0101011
0000000
1110100
0110001 The use of MD
1
• It can be used from atomic scale until
0
planetoid scale -- amazing
• To calculate electronic ground state as
function of time of liquid metal (Kresse and
Hafner, 1993)
• Motion of n-Alkanes molecules (Ryckaert,
Ciccotti, and Berendsen, 1977)
v2011.09.20 FI3102 Computational Physics 5

6. 0101011
0000000
1110100
0110001 The use of MD (cont.)
1
• Nanodroplet on a surface (Sedighi, Murad,
0
and Aggarwal, 2010)
• Grain of in mm and cm size (Gallas,
Herrmann, Pöschel, and Sokolowski,
1996)
• Simulation of asteroids movement (Jaffé,
Ross, Lo, Marsden, Farrelly, and Uzer,
2002)
v2011.09.20 FI3102 Computational Physics 6

7. 0101011
0000000
1110100
0110001 Experiment using simulation
1
0
(Allen, 2004)
v2011.09.20 FI3102 Computational Physics 7

8. 0101011
0000000
1110100
0110001 Experiment using .. (cont.)
1
• It is a bridge between microscopic and
0
macroscopic
• It is also a bridge between theory and
experiment
• Do the experiment using simulation is a
smart way to reduce the financial problem
• Even all considered nature laws are input
to the system, it could give the unexpected
v2011.09.20 FI3102 Computational Physics 8

9. 0101011
0000000
1110100
0110001 Molecular scale
1
• Lennard-Jones potential:
0
• Coulomb potential
v2011.09.20 FI3102 Computational Physics 9

10. 0101011
0000000
1110100
0110001 Molecular scale (cont.)
1
• Can you derive the expression for the
0
forces from both potential?
• MD simulation need expression in term of
force instead of potential
• Use the relation
r r
F = −∇V
v2011.09.20 FI3102 Computational Physics 10

11. 0101011
0000000
1110100
0110001 Molecular scale (cont.)
1
• And the results?
0
r
FLJ =
r
FC =
v2011.09.20 FI3102 Computational Physics 11

12. 0101011
0000000
1110100
0110001 Human scale
1
• Near on earth surface: gravitational force
0
Fg = -mg
• Friction force : Ff = -bv
• Magnetic force : FB = qv ×B
v2011.09.20 FI3102 Computational Physics 12

13. 0101011
0000000
1110100
0110001 Planetoid scale
1
• Newton’s law of universtal gravitation
0
r m1 m 2
FG = −G 2 r ˆ
r
(Wikipedia, 2011)
v2011.09.20 FI3102 Computational Physics 13

14. 0101011
0000000
1110100
0110001 MD algorithm
1
• It is uses Newton’s second law of motion
0
to get the acceleration a
• It using numerical integration to get the
equation of motion, use the simple method
i.e. original Euler method
• New motion parameters will cause new
value of all forces
• Calculate the new forces to get new a
v2011.09.20 FI3102 Computational Physics 14

15. 0101011
0000000
1110100
0110001 MD algorithm (cont.)
1
r r
0
∑ F = ma
r r r r r
∑ F = FG + FB + F f + FLJ + ..
v2011.09.20 FI3102 Computational Physics 15

16. 0101011
0000000
1110100
0110001 MD algorithm (cont.)
1
• Euler method:
0
r r r
vi + 1 = vi + ai ∆t
r r r
ri + 1 = ri + vi ∆t
t i +1 = t i + ∆t
v2011.09.20 FI3102 Computational Physics 16

17. 0101011
0000000
1110100
0110001 MD algorithm (cont.)
1
• You must pay attention to the outside
0
influence that changes with order of
magnitude of chosen ∆t
• Normally it is chose that ∆t must be 100
times smaller than that change
v2011.09.20 FI3102 Computational Physics 17

18. 0101011
0000000
1110100
0110001 Example
1
• Write the numerical expression for a
0
parabolic motion when air friction is
considered
• g=-gj
• r0, v0
• b is for Ff = - bv
v2011.09.20 FI3102 Computational Physics 18

19. 0101011
0000000
1110100
0110001 Example (cont.)
1
• Write the numerical expression for a
0
charged particle that moves perpendicular
to external magnetic field B, initial velocity
is v0 at r0
v2011.09.20 FI3102 Computational Physics 19

20. 0101011
0000000
1110100
0110001 Is MD so perfect?
1
• Unfortunately not
0
• It has problem even all forces are already
considered
• It can produce unreported results or
unexpected (wrong) results
• It has problem in time stamp
v2011.09.20 FI3102 Computational Physics 20

21. 0101011
0000000
1110100
0110001 Time stamp problem
1
• Nanodroplet (Sedighi, Murad, and
0
Aggarwal, 2010):
v2011.09.20 FI3102 Computational Physics 21

22. 0101011
0000000
1110100
0110001 Time stamp problem (cont.)
1
• continue from previous
0
v2011.09.20 FI3102 Computational Physics 22

23. 0101011
0000000
1110100
0110001 Time stamp problem (cont.)
1
• Granular oscillation (Chen, Lin, Li, and Li,
0
2009):
v2011.09.20 FI3102 Computational Physics 23

24. 0101011
0000000
1110100
0110001 Time stamp problem (cont.)
1
0
v2011.09.20 FI3102 Computational Physics 24

25. 0101011
0000000
1110100
0110001 References
1
1. Wikipedia contributors, “Molecular dynamics”, Wikipe-
0 dia, The Free Encyclopedia, 5 September 2011, 15:49
UTC, oldid:448597141 [2011.09.21 09.34+07]
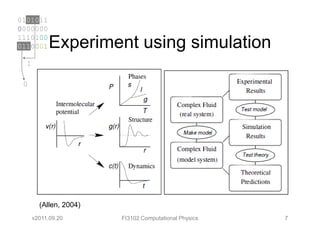
2. Michael P. Allen, “Introduction to Molecular Dynamics
Simulation”, in Computational Soft Matter: From
Synthetic Polymers to Proteins, Lecture Notes, Norberg
Attig, Kurt Binder, Helmut Grubmüller, Kurt Kremer
(Eds.), John von Nuemann Institut for Computing,
Jülich, NIC Series, Vol. 23, pp. 1-28, 2004
v2011.09.20 FI3102 Computational Physics 25

26. 0101011
0000000
1110100
0110001 References (cont.)
1
3. Furio Ercolessi, “A Molecular Dynamics Primer”, Spring
0 College in Computational Physics, ICTP, Trieste,
9/10/1997 URI http://www.fisica.uniud.it/~ercolessi/md
/md/node6.html [2011.09.21 09.51+07]
4. Martin Karplus and J. Andrew McCammon, “Molecular
Dynamics Simulations of Biomolecules”, Nature
Structural Biology 9 (9), 646-653 (2002)
5. G. Kresse and J. Hafner, “Ab Initio Molecular Dynamics
for Liquid Metals”, Physical Review B 47 (1), 558-561
(1993)
v2011.09.20 FI3102 Computational Physics 26

27. 0101011
0000000
1110100
0110001 References (cont.)
1
6. Jean Paul Ryckaert, Giovanni Ciccotti, and Herman J.
0 C. Berendsen, “”Numerical Integration of the Cartesian
Equations of Motion of a System with Constraints:
Molecular Dynamics of n-Alkanes”, Journal of
Computational Physics 23 (3), 327-341 (1977)
7. Jason A. C. Gallas, Hans J. Herrmann, Thorsten
Pöschel, and Stefan Sokolowski, “Molecular Dynamics
Simulation of Size Segregation in Three Dimensions”,
Journal of Statistical Physics 82 (1-2), 443-450 (1996)
v2011.09.20 FI3102 Computational Physics 27

28. 0101011
0000000
1110100
0110001 References (cont.)
1
8. Charles Jaffé, Shane D. Ross, Martin. W. Lo, Jerrold
0 Marsden, David Farrelly, and T. Uzer, “Statistical
Theory of Asteroid Escape Rates”, Physical Review
Letters 89 (1), 011101 (2002)
9. Nahid Sedighi, Sohail Murad, and Suresh K. Aggarwal,
“Molecular Dynamics Simulations of Nanodroplet
Spreading on Solid Surfaces, Effect of Droplet Size”,
Fluid Dynamics Research 42 (3), 035501 (2010)
10. Kuo-Ching Chen, Chi-Hao Lin, Chia-Chieh Li, and Jian-
Jhih Li, “Dual Granular Temperature Oscillation of a
Compartmentalized Bidisperse Granular Gas”, Journal
of the Physical Society of Japan 78 (4), 044401 (2009)
v2011.09.20 FI3102 Computational Physics 28

29. 0101011
0000000
1110100
0110001
1
0
Thank you
(for your patience)
v2011.09.20 FI3102 Computational Physics 29