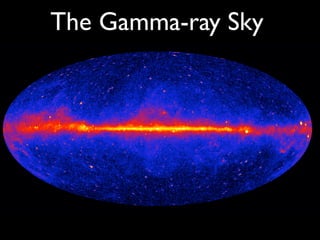
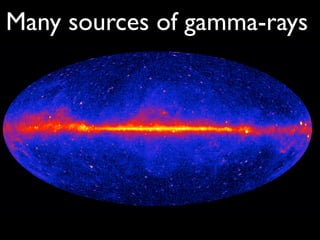
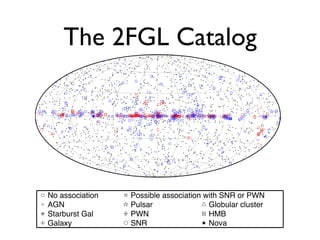
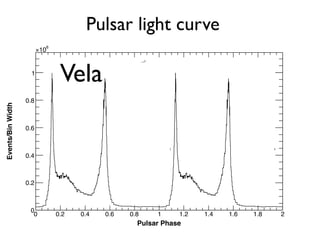
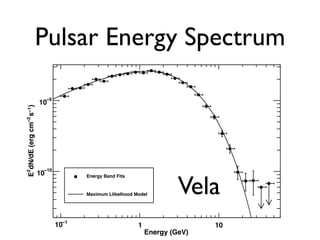
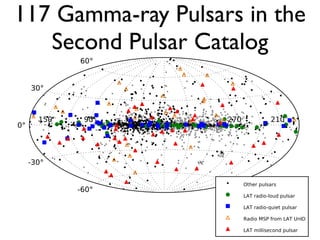
The document discusses neutron star-powered nebulae, particularly pulsar wind nebulae (PWNe), using data from the Fermi Gamma-Ray Space Telescope. It details the historical context of gamma-ray astronomy, the characteristics of pulsars, and the methodologies for identifying and analyzing gamma-ray emissions from these astronomical phenomena. Additionally, the text highlights the challenges in detecting new PWNe and their connections to supernova remnants and other astrophysical sources.

1. Neutron Star Powered
Nebulae: a NewView on
Pulsar Wind Nebulae with the
Fermi Gamma-ray Space
Telescope
Joshua Lande
@joshualande

2. Please ask questions!!

3. Why do we do
astronomy?

4. Nabta Playa 5th century BC

6. Liberal Arts
The Trivium
•grammar
•logic
•rhetoric
The Quadrivium
•arithmetic
•geometry
•music
•astronomy

7. Multiwavelenth
astronomy

8. We can study astronomy across the
electromagnetic spectrum

9. William Herschel 1800
Infrared Astronomy Radio-wave Astronomy
Karl Jansky 1933

10. ultraviolet - 1946
X-ray - 1949

11. Gamma-ray
Astrophysics

12. Explorer XI

13. OSO-3

14. OSO-3: 621 gamma-rays

15. COS-B
SAS-2

16. Cos-B Skymap

17. EGRET

18. EGRET Sky Map

19. The Fermi Gamma-ray
Space Telescope

20. The Fermi Gamma-ray
Space Telescope
20 MeV to >300 GeV

21. The Large Area Telescope
Tracker
Layers
Calorimeter Layers
Anti-Coincidence Detector (surrounding)
Large Area Telescope (LAT)
Fermi Gamma-ray Space
Telescope
photon
positron
electron

23. Angular Resolution of the LAT

25. Blastoff!

26. The Gamma-ray Sky

27. Very High Energy
Astrophysics

28. Very High Energy Astrophysics

30. The High Energy Stereoscopic System
(H.E.S.S)

31. Fermi ~ 20 MeV to 300 GeV
Air Cherenkov Detectors ~100 GeV and ~30 TeV

32. Astrophysical Sources
of Gamma-rays

33. Many sources of gamma-rays

34. The 2FGL Catalog
No association Possible association with SNR or PWN
AGN Pulsar Globular cluster
Starburst Gal PWN HMB
Galaxy SNR Nova

35. Pulsars, Supernova Remnants, and PWNe
are connected through a simple picture
Gaensler & Slane (2006)

36. Supernova
are new stars
that appear in
the sky.
~L|F
Left: SN 1054
(Crab Nebula)

37. 7 supernova
visible by the
human eye in
~2,000 years.
Right: SN 1572
(Tycho’s SN)

38. Pulsars are the
remaining core
of neutron
Stars

40. Pulsars have
periodic emission

41. Pulsar Wind Nebula (PWN) are observed
to surround pulsars

42. Energy Spectrum of the
Crab Nebula

43. Radiation Processes in
PWN

45. Gamma-ray
Observations

46. How to identify Gamma-ray Pulsars?
Vela

47. Pulsar Phase
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
Events/BinWidth
0
0.2
0.4
0.6
0.8
1
6
10×
0.12 0.13 0.14
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
6
10×
0.54 0.56 0.58
0.6
0.7
0.8
0.9
1
6
10×
Pulsar light curve
Vela

48. Energy (GeV)
−1
10 1 10
)−1
s−2
dN/dE(ergcm2
E
−10
10
−9
10
Energy Band Fits
Maximum Llikelhood Model
Pulsar Energy Spectrum
Vela

49. 117 Gamma-ray Pulsars in the
Second Pulsar Catalog

50. Gamma-ray PWN
Crab Nebula
Vela X
Abdo et al 2010
Abdo et al 2010

51. Crab Nebula
:26 (8pp), 2012 April 10 Buehler et al.
Pulsar phase
0.4 0.6 0.8
Pulsar phase
0.4 0.6 0.8 Figure 2. Spectral energy distribution for the Crab Nebula averaged over the
first 33 months of Fermi observations. The axis on the right side indicates the
1260 ABDO ET AL. Vol. 708
Figure 4. Counts maps (arbitrary units) presenting the pulsed (top row) and nebular (bottom row) emission, in three energy bands. Each panel spans 15◦ × 15◦ in
equatorial coordinates and is centered on the pulsar radio position. Left: 100 MeV < E < 300 MeV; middle: 300 MeV < E < 1 GeV; right: E > 1 GeV.
(A color version of this figure is available in the online journal.)
Abdo et al 2010 Abdo et al 2010

52. How do we know it is a PWN?
aharonian et al 2005
•PWN should have rising spectrum
•PWN can be extended
•Clear identification difficult:
•X-ray PWN often much smaller
•Pulsars can be offset
•other possible counterparts
•Pulsar energetics?
•PWN candidate vs clear detection?
•Energy dependent morphology
•Matching X-ray to Gamma-ray
mormorphology?
L26 F. A. Aharonian et al.: The association of HESS J1825–137 with G 18.0–0.7
1. Introduction
PSR B1823–13 (also known as PSR J1826–1334) is a 101 ms
evolved pulsar with a spin-down age of T = 2.1 × 104
years
(Clifton et al. 1992) and in these properties very similar to the
Vela pulsar. It is located at a distance of d = 3.9 ± 0.4 kpc
(Cordes & Lazio 2002) and ROSAT observations of this source
with limited photon statistics revealed a compact core, as well
as an extended diffuse nebula of size ∼5 south-west of the pul-
sar (Finley et al. 1998). High resolution XMM-Newton obser-
vations of the pulsar region confirmed this asymmetric shape
and size of the diffuse nebula, which was hence given the name
G 18.0–0.7 (Gaensler et al. 2003). For the compact core with
extent RCN ∼ 30 (CN: compact nebula) immediately sur-
rounding the pulsar, a photon index of ΓCN = 1.6+0.1
−0.2 was mea-
sured with a luminosity of LCN ∼ 9d2
4 × 1032
erg s−1
in the 0.5
to 10 keV range for a distance of 4d4 kpc. The corresponding
pulsar wind shock radius is Rs ≤ 15 = 0.3d4 pc. The com-
pact core is embedded in a region of extended diffuse emission
which is clearly one-sided, revealing a structure south of the
pulsar, with an extension of REN ∼ 5 , (EN: extended nebula)
whereas the ∼4 east-west extension is symmetric around the
north-south axis. The spectrum of this extended component is
-5
0
5
10
15
20
25
30
-14
-13.5
18h24m18h26m18h28m
PSR B1823-13
RA (hours)
)°Dec ( 3EG J1826-1302
PSF
HESS J1825-137
Fig. 1. Excess map of the region close to PSRB1823–13 (marked with
a triangle) with uncorrelated bins. The best fit centroid of the γ-ray
excess is shown with error bars. The black dotted circle shows the
LettertotheEditor

53. Many TeV Pulsar Wind Nebula
•Many PWN detected
at TeV energies
•Limited Background,
•Improved sensitivity
•No Pulsar signal
•32 TeV PWN

54. Harder at Gamma-ray
energies
•Limited Angular Resolution
•Large Galactic Background
•Non-linear Detector response
•Emission could be from the pulsar.
•Crowded gamma-ray sky

55. How do we search for new
gamma-ray emitting PWN?
Association
with LAT-
detected
Association
with TeV PWN
Spatial
Morphology

56. Extended Fermi
Sources

57. You can study extended LAT sources
using maximum-likelihood analysis
ering events). The likelihood function
d emission:
L =
Y
j
✓
kj
j e ✓j
kj!
.
tion and energy bins, kj are the counts
ts predicted in the same bin.
re computed by integrating the di↵ere
~⌦0
at a time t0
. The dispersion is written as P(E0
, t0
, ~⌦0
|E, t, ~⌦). It repre
probability and is therefore normalized such that
Z Z Z
dEd⌦dtP(E0
, t0
, ~⌦0
|E, t, ~⌦) = 1
Therefore, P(E0
, t0
, ~⌦0
|E, t, ~⌦) has units of 1/energy/SA/time
The convolution of the model a source with the IRFs produces the expec
ferential counts (counts per unit energy/time/SA) that are reconstructed to
energy E0
at a position ~⌦0
and at a time t0
:
⌧(E0
, ~⌦0
, t0
| ) =
Z Z Z
dE d⌦ dt F(E, t, ~⌦| )✏(E, t, ~⌦)P(E0
, t0
, ~⌦0
|E, t, ~⌦)
Here, this integral is performed over all energies, SAs, and times.
For LAT analysis, we conventionally make the simplifying assumption t
Here, j refers to a sum over position and energy bins, kj a
bin j, and ✓j are the model counts predicted in the same b
The model counts in bin j are computed by integrat
counts over the bin:
✓ij =
Z
j
dE d⌦ dt ⌧(E, ~⌦, t| i).
Here, j represents the integral over the jth position/energ
source, i refers to the parameters defining the ith source, a
1 0
plicated hypothesis and H0 th
mpare the likelihood when ass
ended spatial model:
TSext = 2 log(Lext/Lps).
n be written as:
L = L( ).
ysis, one typically fits parameters of a model
ction of the parameters of the model.
max = arg maxL( )

58. 0◦
0.◦
1 0.◦
2 0.◦
3 0.◦
4 0.◦
5 0.◦
6
Extension
10000
10200
10400
10600
10800
11000
11200TestStatistic
(a)
102
103
104
105
Energy (MeV)
0
50
100
150
200
TSext
(b)
0.0 0.1 0.2 0.3 0.4 0.5
∆θ2
([deg]2
)
101
102
103
Counts
(c)
Disk
Point
Counts
(d)
2◦
3◦
b
188◦
189◦
l
0
500
1000
1500
2000
2500
3000
3500
counts[deg]−2
Extended
Source IC 443

59. Search each source in
2FGL for extension

60. IC 443
Puppis A
W44
MSH 15−52
W51C
W28
SMC
Gamma Cygni
Vela X
Cygnus Loop
Vela Jr.
LMC
RX J1713.7−3946
HESS J1825−127
W30
Centarus A
New Extended Sources

61. 0
1b
2526
l
0
25
50
75
100
125
150
175
200
225
counts/[deg]2
HESS J1837-069

62. 1 000
0 300
0 000
0 300
b
331 300
332 000
332 300
333 000
l
0
30
60
90
120
150
180
210
240
270
counts/[deg]2
HESS J1616−508

63. 1
0
1
b
336337
l
0
30
60
90
120
150
180
210
240
270
counts/[deg]2
HESS J1632-478

64. 10−6
10−5
E2
dN/dE(MeVcm−2
s−1
)
(a) HESS J1616−508 (b) HESS J1614−518
LAT
H.E.S.S
104
105
106
107
Energy (MeV)
10−6
10−5
E2
dN/dE(MeVcm−2
s−1
)
(c) HESS J1632−478
104
105
106
107
Energy (MeV)
(d) HESS J1837−069

65. PWN Search in the
Off-Peak

66. Search LAT-detected
pulsars for PWN

67. 0.0 0.2 0.4 0.6 0.8 1.0
0
100
200
300
400
500
600
700
800
Counts
0.0 0.2 0.4 0.6 0.8 1.0
0
100
200
300
400
0.0 0.2 0.4 0.6 0.8 1.0
0
50
100
150
200
250
300
350
Counts
0.0 0.2 0.4 0.6 0.8 1.0
0
100
200
300
400
500
0.0 0.2 0.4 0.6 0.8 1.0
Phase
0
100
200
300
400
500
600
700
Counts
0.0 0.2 0.4 0.6 0.8 1.0
Phase
0
5
10
15
20
25
30
35
We can define
the off-peak
region using a
Bayesian Block
decomposition
of the pulsar
light curve

68. Is it a pulsar or a PWN?Grondin et al.
Energy [MeV]
3
10 4
10
5
10
6
10 7
10
]-1s-2
dN/dE[ergcm2
E
-12
10
-11
10
-10
10
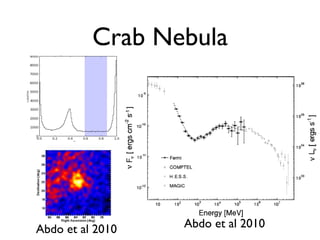
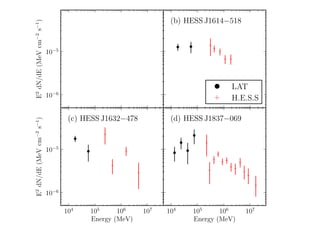
pectral energy distribution of HESS J1825−137 in gamma-rays. The LAT spectral points (in red) are obtained using the maximum likelihood
described in section 4.2 in 6 logarithmically-spaced energy bins. The statistical errors are shown in red, while the black lines take into account both
nd systematic errors as discussed in section 4.2. The red solid line presents the result obtained by fitting a power-law to the data in the 1 – 100 GeV
using a maximum likelihood fit. A 95 % C.L. upper limit is computed when the statistical significance is lower than 3 σ. The H.E.S.S. results are
blue (Aharonian et al. 2006).
pulsar, we fix the initial spin period at 10 ms and
ex at 2.5, yielding an age of 26 kyr for the sys-
simple injection spectrum slightly underestimates
ata but the overall fit is still reasonable. For the
of 26 kyr, we require a power-law index of 1.9,
57 TeV and a magnetic field of 4 µG. The corre-
sult is presented in Figure 4 (Top).
option to fit the multi-wavelength data is adopting
tic Maxwellian plus power-law tail electron spec-
sed by Spitkovsky (2008). For this injection spec-
sume a bulk gamma-factor (γ0) for the PWN wind
f the termination shock. At the termination shock
t pressure balances the wind pressure, fully ther-
e wind; in this case the downstream post-shock
= (γ0 − 1)/2. One could also interpret this as
e temperature kT of mec2
(γ0 − 1)/2. Per the
of Spitkovsky (2008), a power-law tail begins at
mec2
γ0, and suffers an exponential cutoff at some
The Fermi LAT Collaboration acknowledges generous ongoing support
from a number of agencies and institutes that have supported both the de-
velopment and the operation of the LAT as well as scientific data analysis.
These include the National Aeronautics and Space Administration and the
Department of Energy in the United States, the Commissariat `a l’Energie
Atomique and the Centre National de la Recherche Scientifique / Institut Na-
tional de Physique Nucl´eaire et de Physique des Particules in France, the
Agenzia Spaziale Italiana, the Istituto Nazionale di Fisica Nucleare, and the
Istituto Nazionale di Astrofisica in Italy, the Ministry of Education, Culture,
Sports, Science and Technology (MEXT), High Energy Accelerator Research
Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in
Japan, and the K. A. Wallenberg Foundation and the Swedish National Space
Board in Sweden. Additional support for science analysis during the opera-
tions phase from the following agencies is also gratefully acknowledged: the
Instituto Nazionale di Astrofisica in Italy and the Centre National d’´Etudes
Spatiales in France.
The Nanc¸ay Radio Observatory is operated by the Paris Observatory, associ-
ated with the French Centre National de la Recherche Scientifique (CNRS).
The Lovell Telescope is owned and operated by the University of Manchester
as part of the Jodrell Bank Centre for Astrophysics with support from the
Science and Technology Facilities Council of the United Kingdom.
The Parkes radio telescope is part of the Australia Telescope which is funded
– 37 –
Energy (MeV)
2
10
3
10
4
10
]-1
s-2
dN/dE[ergcm2
E
-11
10
-10
10
1
]-1
s-2
dN/dE[ergcm2
E
-12
10
-11
10
Energy (MeV)
2
10
3
10 10
]-1
s-2
dN/dE[ergcm2
E
-12
10
-11
10
4 Grondin et al.
HESS J1825-137
(Grondin et al 2011)
PSR J2021+4026
Ackermann et al 2010
HESS J1825-137
(Grondin et al 2011)
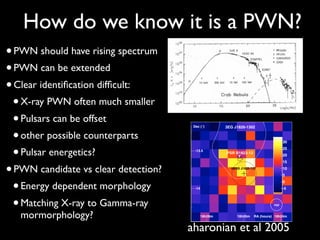
Spectral Shape:
• Pulsars are cutoff
• PWN rising spectrum
Morphology
• Pulsars are point sources
• PWN could be extended

69. 10 13
10 12
10 11
10 10
10 9
10 13
10 12
10 11
10 10
E2
dN/dE(ergcm2
s1
)
10 13
10 12
10 11
10 10
10 9
10 1
100
101
102
Energy (GeV)
10 1
100
101
102
Energy (GeV)
We
performed
a spectral
and spatial
analysis of
each off-
peak region

70. Off-peak Sources
•116 pulsars tested
•34 significant sources
•9 are clearly pulsar emission
•4 are pulsar wind nebula
•1 new pulsar wind nebula

71. 3C 58 is
associated and
PSR J0205+6449
Coincident with
SNR 3C 58 and
SN 1181

72. Search for TeV PWN

74. HESS J1303-613
1
0
1
b
262728
l
0
20
40
60
80
100
120
140
160
180
counts/[deg]2
HESS J1841-055
1
0
b
292293
l
0
10
20
30
40
50
60
70
80
90
counts/[deg]2
HESS J1119-614 HESS J1356-645
0
1
b
313314
l
0
25
50
75
100
125
150
175
200
225 counts/[deg]2
HESS J1420-607

75. PWN Detected by LAT
•Before Fermi, 1 PWN Detected (Crab)
•Now, 17 PWN candidates
•5 clearly associated with PWN
•12 have less certain identification.

76. PWN Population Study

77. 102
103
104
105
106
107
108
109
1010
1011
⌧C [years]
1028
1029
1030
1031
1032
1033
1034
1035
1036
1037
1038
1039
˙E[ergs1
]
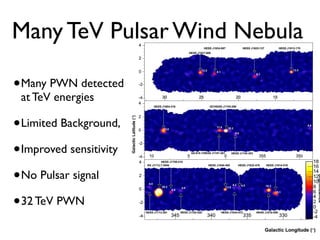
LAT Detects
PWN from
young and
highly-
energetic
pulsars

78. 1034
1035
1036
1037
1038
1039
˙E
1032
1033
1034
1035
1036
LGeV
The PWN
Luminosity is
small compared
to the pulsar’s
spin-down
energy

79. 1033
1034
1035
1036
LGeV(ergs1
)
103
104
105
Age (yr)
100
101
102
LGeV/LTeV
1035
1036
1037
1038
1039
˙E (erg s 1
)
LGeV and LGeV/LTeV
not correlated with
age and spin-down
energy

80. 1031
1032
1033
1034
1035
1036
1037LX(ergs1
)
103
104
105
Age (yr)
10 2
10 1
100
101
102
103
104
LGeV/LX
1035
1036
1037
1038
1039
˙E (erg s 1
)
LGeV/LX
correlates
with the age
and spin-
down
energy

81. The lifetime of gamma-ray emitting
electrons is longer than of X-ray
emitting electrons.EVOLUTION OF THE γ - AND X-RAY LUMINOSITIES OF PWNe
102
103
104
105
Time (yr)
0.01
0.10
1.00
Normalizednumberofparticles
nγnX
tcγtcX 10-1
100
101
102
103
104
Rationγ/nX
nγ /nX
Mattana et al 2009

82. Conclusions

83. Acknowledgments

84. Stanford Physics

86. The LAT Collaboration

87. Big thanks to my
defense committee!

88. The Funk
Group

90. Thanks to my family!

91. Thanks to the
administrators!

92. Finally, thanks for
coming!

93. Questions?