This document presents an internship project report on multistep methods for solving initial value problems of ordinary differential equations. It introduces the basic problem of finding the function y(t) that satisfies a given differential equation and initial condition. It discusses existence and uniqueness theorems, Picard's method of successive approximations, and approaches for approximating the required integrations, including the derivative, Taylor series, and Euler's methods. The report appears to evaluate various one-step and multistep numerical methods for solving initial value problems, including Runge-Kutta, Adams-Bashforth, and Adams-Moulton methods.

1. 1
MULTISTEP METHODS FOR
INITIAL VALUE PROBLEMS
NPDE-TCA
INTERNSHIP PROJECT REPORT
BY
RISHAV RAI
INDIAN INSTITUTE OF TECHNOLOGY
GUWAHATI
Supervisor: Dr. Sarvesh Kumar
Department of Mathematics
Indian Institute of Space Science and Technology, IIST
Thiruvananthapuram
December 2015

2. 2
BONAFIDE CERTIFICATE
This is to certify that this project report entitled “Multistep Methods for Initial
Value Problems” submitted to Indian Institute of Space Science and
Technology, Thiruvananthapuram, is a bonafide record of work done by
Rishav Rai under my supervision from 10th
to 31st
December.
Place: Thiruvananthapuram
Date: 31/12/2015
Signature

3. 3
DECLARATION BY AUTHOR
This is to declare that this report has been written by me. No part of the report is
plagiarized from other sources. All information included from other sources have
been duly acknowledged.
I aver that if any part of the report is found to be plagiarized, I shall take full
responsibility for it.
Mr. Rishav Rai
Pursuing B.Tech in Mechanical Engineering (3rd
Year)
Indian Institute of Technology Guwahati.
India.
Signature of author
Place: Thiruvananthapuram
Date: 31/12/2015

4. 4
ACKNOWLEDGEMENT
I wish to express my sincere thanks to National Program on Differential Equation:
Theory, Computation and Applications (NPDE-TCA) for providing me an
opportunity to do Winter Internship 2015 at IIST Thiruvananthapuram and
providing me with the required facilities.
I sincerely thank Dr. Sarvesh Kumar, Assistant Professor, Department of
Mathematics IIST, for guiding me throughout the project.
I would also like to express my heartfelt thanks to the IIST Thiruvananthapuram
Administration for providing me with the necessary facilities and for making my
stay comfortable.

5. 5
TABLE OF CONTENTS
1. Chapter 1: Introduction 07
1.1. The Basic Mathematical Equation 08
1.2. Basic Existence and Uniqueness Theorem 09
1.3. Picard’s Theorem. 09
1.4. Picard’s Methods of Successive Approximations. 09-10
1.5. Lipchitz Condition. 10
1.6. Approaches for approximating the integration. 11
1.7. Derivative Approach. 11
1.8. Taylor Series. 12
1.9. Types of Errors. 12-13
2. Chapter 2: One-Step and Multistep Methods 14
2.1. Explicit and Implicit. 14
2.2. Euler’s Method. 14
2.2.1.Matlab code and simulation 15-16
2.3. Trapezoidal’s Method. 16
2.3.1.Matlab code and simulation 16-17
2.4. Simpson’s Method. 18
2.4.1. Matlab code and simulation 18
2.5. Runge-Kutta’s Methods. 19
2.5.1.Runge-Kutta 2nd
Order Method. 19
2.5.1.1. Heun’s Method. 20
2.5.1.2. Mid-Point Method. 20
2.5.1.3. Ralston’s Method. 20
2.5.1.4. Matlab Simulation of above three methods. 21-22
2.5.2.Runge-Kutta 4th
Order Method. 23
2.5.2.1. RK4 Method by Runge. 23
2.5.2.2. Kutta’s Method. 25
2.5.2.3. Matlab Code and simulation of above two methods.25

6. 6
3. Chapter 3: Multistep Methods 26
3.1. Adams-Basforth Methods. 26
3.1.1. Adams-Basforth 2-step Method. 26
3.1.2. Adams-Basforth 2-step Method Matlab code and simulation.27
3.1.3. Adams-Basforth 3-step Method. 28
3.1.4. Adams-Basforth 2-step Method Matlab code and simulation.29
3.2. Adams-Moulton Methods. 29
3.2.1. Adams-Moulton 2-step Method. 29
3.2.2. Adams-Moulton 3-step Methods. 30
3.2.3. Matlab code and simulation for above two methods. 30-31
4. Chapter 4: Predictor Collector Methods. 32
5. Chapter 5: Convergence, Consistency and Stability for Modified Euler
Method. 33-34
6. Chapter 6: Linear Multistep Methods. 34
7. Chapter 7. Conclusion. 35
8. Chapter 8. Bibliography. 36

7. 7
INTRODUCTION
DEFINITION:
An equation involving derivatives of one or more dependent variables with respect
to one or more independent variables is called a differential equation.
Example-
𝑑(𝑒 𝑘𝑥)
𝑑𝑥
= 𝑘𝑒 𝑘𝑥
;
𝑑(𝑚𝑛)
𝑑𝑥
=
𝑚𝑑(𝑛)
𝑑𝑥
+
𝑛𝑑(𝑚)
𝑑𝑥
.
A differential equation involving ordinary derivatives of one or more dependent
variables with respect to single independent variable is called an ordinary
differential equation.
Example-
𝑑3 𝑦
𝑑𝑥3 + 𝑥𝑦(
𝑑𝑦
𝑑𝑥
)3
= 0 ;
𝑑4 𝑥
𝑑𝑡4 +
5𝑑2 𝑥
𝑑𝑡2 + 3𝑥 = sin 𝑡
A differential equation involving partial derivatives of one or more dependent
variables with respect to more than one independent variable is called a partial
differential equation.
Example-
𝜕𝑦
𝜕𝑥
+
𝜕𝑦
𝜕𝑡
= 𝑡 ;
𝜕2 𝑦
𝜕𝑝2 +
𝜕2 𝑦
𝜕𝑞2 +
𝜕2 𝑦
𝜕𝑟2=0
The order of highest ordered derivative involved in a differential equation is called
the order of the differential equation.
A set of differential equation that describes the behavior of the solution on the
boundary of the region under consideration are called boundary conditions and the
resultant problem is called boundary value problem.
Initial conditions are the conditions which are specified at a single value of the
independent variable, and the combination of a differential equation and a set of
initial conditions is called initial value problem.

8. 8
THE BASIC MATHEMATICAL EQUATION:
In this report we will develop and analyze the various numerical techniques for
approximating the solution of initial value problems of ordinary differential
equations. The basic problem is stated as follows which is a scalar first-order initial
value problem: we have to find the function y (t) that satisfies
y'(t)=ƒ(t, y(t)), a≤ t ≤b; (1.1)
y (𝑡0)=𝑦0.
Where ƒ is a continuous function of t and y in some domain D in t-y plane and let
𝑡0 and 𝑦0 be a point of domain D. To solve this type of differential equation our
goal is to find a function y that not only satisfy the differential equation (1.1) but
also satisfies the initial condition which has value 𝑦0 at t=𝑡0. The geometrical
interpretation of this initial value problem is to find an integral curve of the
differential equation (1.1) that passes through the point (𝑡0, 𝑦0).
NOTATION:
True solution of the differential equation (1.1) is denoted by 𝑦𝑖 at t=𝑡𝑖 and 𝑤𝑖
denotes the approximate solution, 𝑤𝑖 will be approximated to𝑦𝑖.
𝑤𝑖≈ 𝑦𝑖=y ( 𝑡𝑖).

9. 9
BASIC EXISTENCE AND UNIQUENESS THEOREM:
dy
dx
= 𝑓( 𝑥, 𝑦), 𝑦( 𝑥0) = 𝑦0
Where
1. The function 𝑓 is continuous function of x and y in some domain D of x-y
plane.
And
2. The partial derivative
∂𝑓
∂x
is also continuous function of x and y in domain D,
and let (𝑥0,𝑦0) be some point in the domain D.
PICARDS THEOREM:
Let D: |x-𝑥0| < a, |y-𝑦0| <b be a rectangle. Let 𝑓( 𝑥, 𝑦) be continuous and bounded in
D, i.e. there exists a number K such that
|𝑓( 𝑥, 𝑦)| ≤ K ∀ (x, y) ϵ D.
Picard’s theorem tells us about the existence and uniqueness of solutions of first
order differential equations with given initial condition.
PICARD’S METHOD OF SUCCESSIVE APPROXIMATIONS:
Taking the initial value problem of the form
dy
dx
= 𝑓( 𝑥, 𝑦), 𝑦( 𝑥0) = 𝑦0 ... (1.2)
By integrating over the interval (𝑥0, 𝑥), (1.2) gives
∫ 𝑑𝑦
𝑦
𝑦0
= ∫ 𝑓( 𝑥, 𝑦) 𝑑𝑥
𝑥
𝑥0
Or y(x) −𝑦0=∫ 𝑓( 𝑥, 𝑦) 𝑑𝑥
𝑥
𝑥0
y(x) =𝑦0 + ∫ 𝑓( 𝑥, 𝑦) 𝑑𝑥.
𝑥
𝑥0
... (1.3)
y(x) gives the value of true solution of the differential equation at point x, since
we don’t know the information concerning the expression of y in terms of x,
the integral on the R.H.S of (1.3) cannot be evaluated and hence the exact value

10. 10
of y cannot be obtained. So because of this we have to determine a sequence of
approximations to the solution (1.3) as follows. To approximate we put y=𝑦0
in the integral on the right of (1.3) and obtain.
𝑦1(𝑥) = 𝑦0 + ∫ 𝑓( 𝑥, 𝑦0) 𝑑𝑥.
𝑥
𝑥0
... (1.4)
In the above equation 𝑦1(𝑥) represents value of y(x) and is called first
approximation and is better approximation of y(x) at any x. To determine still
better approximation we replace y by 𝑦1 in the integral on the R.H.S in the
(1.3) and obtain the second approximation 𝑦2 as
𝑦2(𝑥) = 𝑦0 + ∫ 𝑓( 𝑥, 𝑦1) 𝑑𝑥.
𝑥
𝑥0
… (1.5)
Going in this sequence, the nth approximation 𝑦𝑛 is given by
𝑦𝑛(𝑥) = 𝑦0 + ∫ 𝑓( 𝑥, 𝑦 𝑛−1) 𝑑𝑥.
𝑥
𝑥0
… (1.6)
An initial value problem that has a unique solution and is stable is said to be well-
posed. An important tool for establishing that an initial value problem is well posed
is the Lipschitz condition.
LIPSCHITZ CONDITION: A function ƒ (t, y) satisfies a Lipschitz Condition in y
on the set D ⊂ 𝑅2
if there exists a constant L > 0 such that
|ƒ (t,𝑦1) −ƒ (t, 𝑦2)| ≤ L|𝑦1 − 𝑦2|
For all (t,𝑦1), (t,𝑦2) ∈ D. The constant L is called the Lipschitz Constant for ƒ.

11. 11
SOME APPROACHES FOR APPROXIMATING THE INTEGRATION:
1- ∫ ƒ( 𝑥) 𝑑𝑥
𝑏
𝑎
= (𝑏 − 𝑎)ƒ(𝑎)
⟹ 𝑦 𝑛+1 = 𝑦𝑛 + ℎƒ(𝑥 𝑛, 𝑦𝑛)
2- ∫ ƒ( 𝑥) 𝑑𝑥
𝑏
𝑎
= (
𝑏−𝑎
2
) [ƒ( 𝑎) + ƒ( 𝑏)]
⟹𝑦 𝑛+1 = 𝑦𝑛 + (
ℎ
2
) [ƒ( 𝑥 𝑛, 𝑦𝑛) + ƒ( 𝑥 𝑛+1, 𝑦 𝑛+1)]
3- ∫ ƒ( 𝑥) 𝑑𝑥
𝑏
𝑎
= (
𝑏−𝑎
6
) [ƒ( 𝑎) + 4ƒ(
𝑎+𝑏
2
) + ƒ( 𝑏)]
⟹ 𝑦 𝑛+1 = 𝑦𝑛 + (
ℎ
6
) [ƒ( 𝑥 𝑛, 𝑦𝑛) + 4ƒ(
𝑥 𝑛+𝑥 𝑛+1
2
,
𝑦 𝑛+𝑦 𝑛+1
2
) + ƒ( 𝑥 𝑛+1, 𝑦 𝑛+1)]
DERIVATIVE APPROACH:
dy
dx
= lim
ℎ→0
𝑦( 𝑥 + ℎ) − 𝑦( 𝑥)
ℎ
Approximating the above differential equation
dy
dx
≈
𝑦( 𝑥 + ℎ) − 𝑦( 𝑥)
ℎ
dy
dx
= ƒ(𝑥, 𝑦)
𝑤1 − 𝑤0
ℎ
= ƒ(𝑥0, 𝑤0)
𝑤1 = 𝑤0 + ℎƒ(𝑥0, 𝑤0)

12. 12
TAYLOR SERIES:
ƒ( 𝑥) = ƒ( 𝑥0) + ( 𝑥 − 𝑥0)ƒ′( 𝑥0) +
(𝑥−𝑥0)2
2!
ƒ′′( 𝑥0) + ⋯
(𝑥−𝑥0) 𝑛
𝑛!
ƒ 𝑛( 𝑥0) + 𝐸
E =
(𝑥−𝑥0) 𝑛+1
(𝑛+1)!
ƒ 𝑛+1( 𝜉)
Where 𝑥0 < 𝜉 < 𝑥.
Hence the true solution from the Taylor Series is:
𝑦𝑖+1 = 𝑦𝑖 + ℎƒ( 𝑥𝑖, 𝑦𝑖) +
ℎ2
2
𝑦′′
(𝜉𝑖)
On removing the error term we will get the approximate solution (we are
approximating up to first order) which is:
𝑤𝑖+1 = 𝑤𝑖 + ℎƒ(𝑥𝑖, 𝑤𝑖)
On approximating up to second order we will get:
𝑤𝑖+1 = 𝑤𝑖 + ℎƒ(𝑥𝑖, 𝑤𝑖) +
ℎ2
2
ƒ′(𝑥𝑖, 𝑤𝑖)
dƒ(x, y)
dx
=
𝜕ƒ
𝜕𝑥
+
𝜕ƒ
𝜕𝑦
ƒ
TYPES OF ERROR’S:
There are two different types of errors involved in the analysis of numerical
methods for initial value problems which either one-step or multistep methods.
Which are as follows:
1-LOCAL TRUNCATION ERROR: It measures how well the difference equation
approximates the solution of the differential equation, it estimates the error
introduced in the single iteration of the method, assuming the solution at previous
steps was exact. It is denoted by the symbol𝜏𝑖.

13. 13
𝜏𝑖 =
𝑦 𝑖+1−𝑦 𝑖
ℎ 𝑖
− 𝜙(ƒ, 𝑡𝑖, 𝑤𝑖, 𝑤𝑖+1, ℎ𝑖) For one-step.
𝜏𝑖 =
𝑦 𝑖+1−∑ 𝑎 𝑗 𝑦 𝑖+1−𝑗
𝑚
𝑗=0
ℎ
− ∑ 𝑏𝑗
𝑚
𝑗=0 ƒ(𝑡𝑖+1−𝑗, 𝑦𝑖+1=𝑗) For multistep method.
2-GLOBAL DISCRETIZATION ERROR: It measures how well the solution of the
difference equation approximates the solution of the differential equation 𝑦𝑖 −
𝑤𝑖. It finds the total of all the errors introduced by all of the time steps taken.
THREE IMPORTANT PROPERTIES FOR A WELL-POSED SOLUTION ARE:
1-CONSISTENCY:
The given solution of the differential equation is said to be consistent if
𝜏𝑖 → 0 𝑎𝑠 ℎ → 0
2-CONVERGENCE:
The given solution of the differential equation is said to be convergent if:
h→0, max|𝑦𝑖 − 𝑤𝑖| → 0
3-STABILITY:
The given solution of the differential equation is said to stable if on doing a
small change in the value of x there is no drastic change in the value of the
dependent variable y.
We can also say that
Convergence ⇔ Stability + Convergent

14. 14
ONE –STEP AND MULTISTEP METHODS
In this report I will consider the two different types of initial value problem which is
one-step methods and multistep methods. The general form of a one-step method is
𝑤 𝑖+1−𝑤𝑖
𝑤 𝑖
= 𝜙(ƒ, 𝑡𝑖, 𝑤𝑖, 𝑤𝑖+1, ℎ𝑖),
The above equation is called difference equation. Where ℎ𝑖 = 𝑡𝑖+1 − 𝑡𝑖 called time
step, 𝑤𝑖 is the approximation of 𝑦𝑖 at t =𝑡𝑖.
EXPLICIT AND IMPLICIT:
If the function ϕ is independent of 𝑤𝑖+1, then the difference equation can be
solved explicitly for 𝑤𝑖+1 , so the method is said to be explicit and when ϕ does
depend of 𝑤𝑖+1 , the difference equation defines the value of 𝑤𝑖+1only
implicitly, so the method is said to be implicit.
EULER’S METHOD:
It is the easiest method for solving ordinary differential equation with the given
initial value.
We want to approximate the solution of the initial value problem
𝑦′( 𝑡) = ƒ(𝑡, 𝑦( 𝑡)), 𝑎 ≤ 𝑡 ≤ 𝑏
𝑦( 𝑎) = 𝛼
Step size h = (b-a)/N 𝑡𝑖 = 𝑎 + 𝑖ℎ (𝑖 = 0,1,2, … . , 𝑁)
From Taylor Series expansion we get
y(t) = 𝑦𝑖 + ( 𝑡 − 𝑡𝑖) 𝑦′𝑖 +
(𝑡 − 𝑡𝑖)2
2
𝑦′′
(𝜉𝑖)
Where t<ξ<𝑡𝑖, so at t=𝑡𝑖+1 the equation becomes
𝑦𝑖+1 = 𝑦𝑖 + ℎƒ( 𝑡𝑖, 𝑦𝑖) +
1
2
ℎ2
𝑦′′(𝜉)

15. 15
We will get the Euler’s method by dropping the error term and replacing
𝑦𝑖(exact solution) by 𝑤𝑖(approximate solution):
𝑤0 = 𝛼
𝑤𝑖+1 = 𝑤𝑖 + ℎƒ(𝑡𝑖, 𝑤𝑖) i=0, 1, 2, 3…, N-1.
Example: In this given example we are going to solve the differential equation with
the given initial value and calculate the error of the approximate solution from the
true solution.
𝑦′( 𝑥) = 𝑒−2𝑥
− 3𝑦 y (0)=5.
𝑦′( 𝑥) + 3𝑦 = 𝑒−2𝑥
Multiplying both sides by integrating factor.
𝑦𝑒3𝑥
= ∫ 𝑒 𝑥
𝑑𝑥
𝑦𝑒3𝑥
= 𝑒 𝑥
+ 𝑐
Using initial condition we get,
𝑦( 𝑥) = 𝑒−3𝑥
(𝑒 𝑥
+ 4)=yexact.
Matlab code of the above example is:
%% Example
% Solve y'(x)=exp(-2*x)-3*y with y0=5 using Eulers's approach
y0=5; % Initial Condition
h = 0.3; % Step size
x = 0:h:6; % x goes from 0 to 6.
yexact = exp(-3*x).*(exp(x)+4) % Exact solution
y=zeros(size(x)) % Preallocate array
y(1)=y0 % Initial condition gives solution at x=0.
for i=1:(length(x)-1) % Using for loop
y(i+1)=y(i)+h*(exp(-2*x(i))-3*y(i)) % Approximate solution for next value of y
end
plot(x,yexact,x,y,x,yexact-y);
xlabel('dependent variable x')
title('Eulers approach')
legend('Exact','Approximate','error');

16. 16
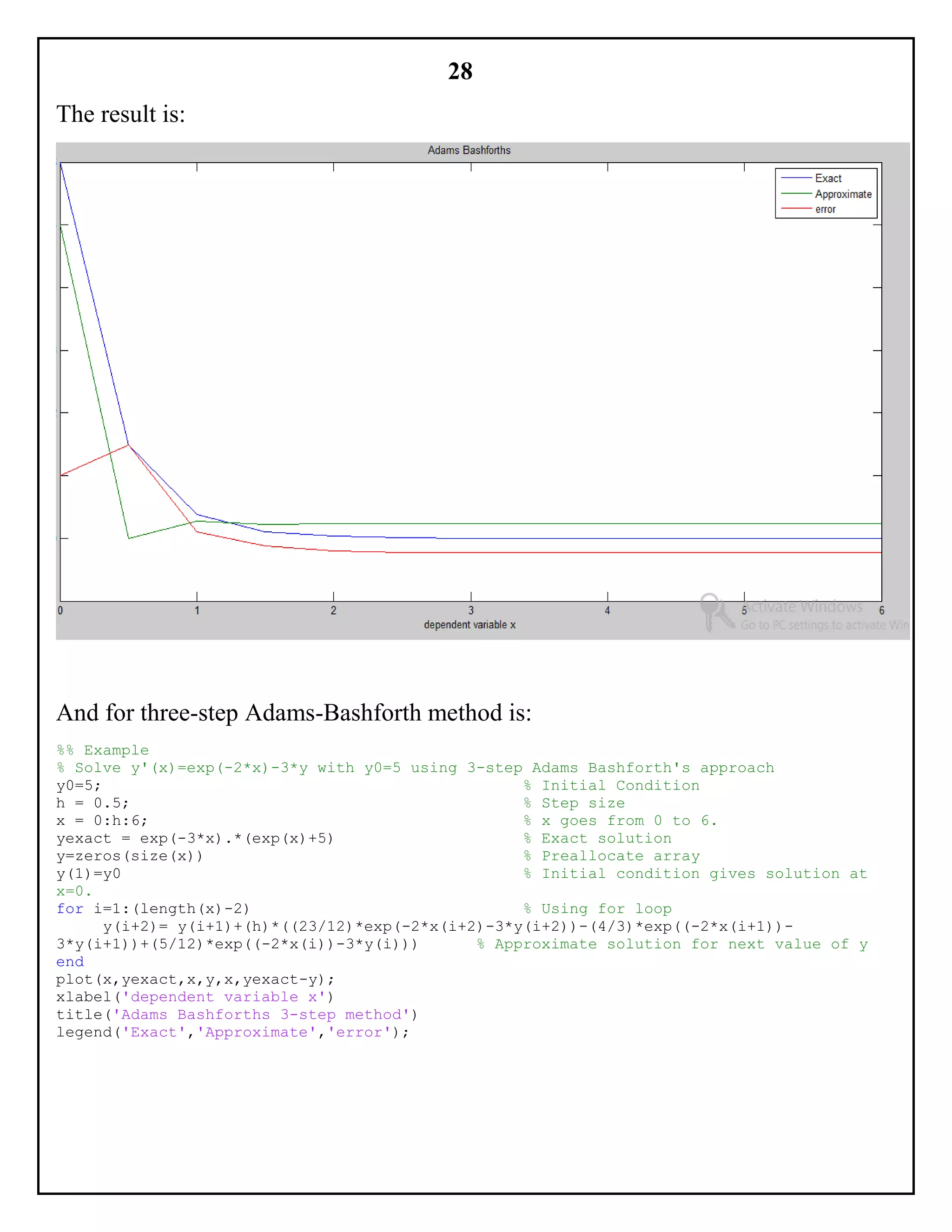
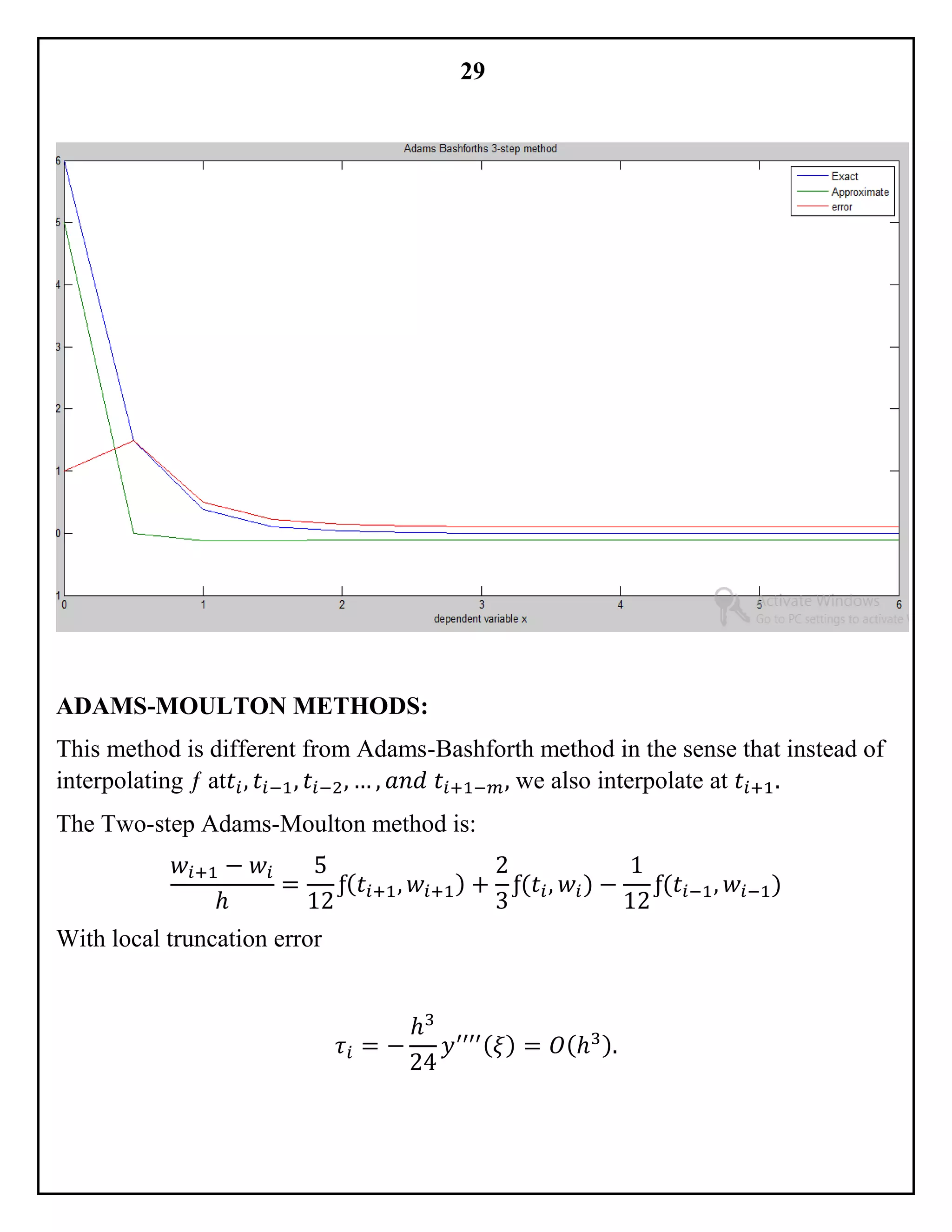
After running the above code, the graph comes out to be:
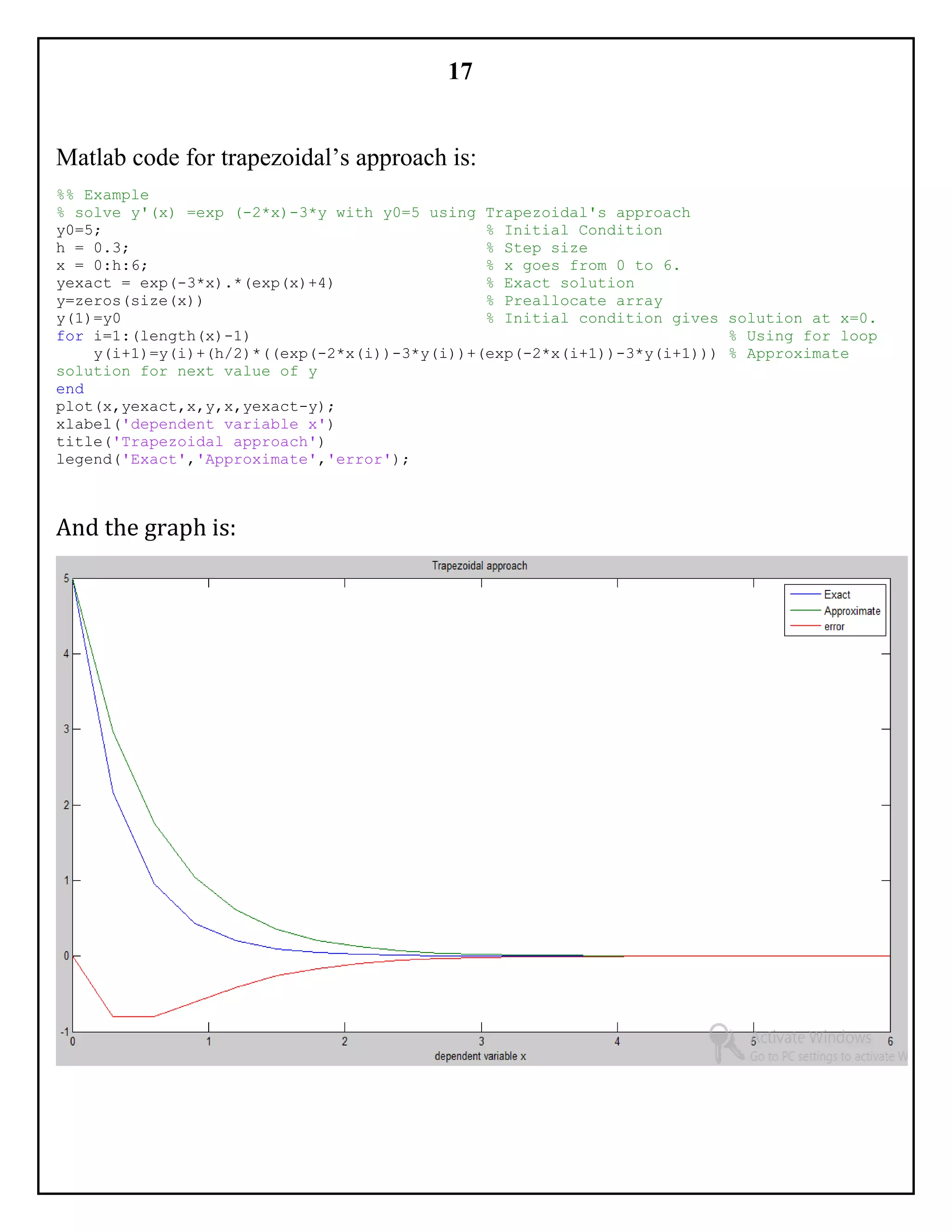
TRAPEZOIDAL’S METHOD:
It’s a method for approximating the definite integral ∫ 𝑓( 𝑥) 𝑑𝑥
𝑏
𝑎
Using linear approximation.
∫ ƒ( 𝑥) 𝑑𝑥
𝑏
𝑎
≈ (
𝑏 − 𝑎
2
) [ƒ( 𝑎) + ƒ( 𝑏)]
𝑦𝑖+1 = 𝑦𝑖 + (
ℎ
2
) [ƒ( 𝑥𝑖, 𝑦𝑖) + ƒ( 𝑥𝑖+1, 𝑦𝑖+1)]

17. 17
Matlab code for trapezoidal’s approach is:
%% Example
% solve y'(x) =exp (-2*x)-3*y with y0=5 using Trapezoidal's approach
y0=5; % Initial Condition
h = 0.3; % Step size
x = 0:h:6; % x goes from 0 to 6.
yexact = exp(-3*x).*(exp(x)+4) % Exact solution
y=zeros(size(x)) % Preallocate array
y(1)=y0 % Initial condition gives solution at x=0.
for i=1:(length(x)-1) % Using for loop
y(i+1)=y(i)+(h/2)*((exp(-2*x(i))-3*y(i))+(exp(-2*x(i+1))-3*y(i+1))) % Approximate
solution for next value of y
end
plot(x,yexact,x,y,x,yexact-y);
xlabel('dependent variable x')
title('Trapezoidal approach')
legend('Exact','Approximate','error');
And the graph is:

18. 18
SIMPSON’S METHOD: It is the method for approximating the integral of a
function using quadratic polynomials. It is generally more accurate than other
numerical methods.
∫ ƒ( 𝑥) 𝑑𝑥
𝑏
𝑎
≈ (
𝑏 − 𝑎
6
) [ƒ( 𝑎) + 4ƒ(
𝑎 + 𝑏
2
) + ƒ( 𝑏)]
𝑦𝑖+1 = 𝑦𝑖 + (
ℎ
6
) [ƒ( 𝑥𝑖, 𝑦𝑖) + 4ƒ(
𝑥𝑖 + 𝑥𝑖+1
2
,
𝑦𝑖 + 𝑦𝑖+1
2
) + ƒ( 𝑥𝑖+1, 𝑦𝑖+1)]
Matlab Code for Simpson’s approach is:
%% Example
% Solve y'(x)=exp(-2*x)-3*y with y0=5 using Simson's approach
y0=5; % Initial Condition
h = 0.3; % Step size
x = 0:h:6; % x goes from 0 to 6.
yexact = exp(-3*x).*(exp(x)+4) % Exact solution
y=zeros(size(x)) % Preallocate array
y(1)=y0 % Initial condition gives solution at x=0.
for i=1:(length(x)-1) % Using for loop
y(i+1)=y(i)+(h/6)*((exp(-2*x(i))-3*y(i))+4*exp(-2*((x(i)+x(i+1))/2)-
3*((y(i)+y(i+1))/2))+exp(-2*(x(i)+x(i+1))-(3*((y(i)+y(i+1)))))) % Approximate solution
for next value of y
end
plot(x,yexact,x,y,x,yexact-y);
xlabel('dependent variable x')
title('simsons approach')
legend('Exact','Approximate','error');

19. 19
RUNGE-KUTTA METHODS:
This methods are class of higher order one-step methods, in numerical analysis
these methods are a family of implicit and explicit iterative methods. These
methods aim to achieve higher accuracy by sacrificing the efficiency of Euler’s
method through re-evaluating ƒ (.,.) at points intermediate between (𝑥 𝑛, 𝑦(𝑥 𝑛)) and
(𝑥 𝑛+1, 𝑦(𝑥 𝑛+1)).
RUNGE-KUTTA 2nd
ORDER METHOD:
The differential equation with initial valve is given as:
dy
dx
= ƒ( 𝑥, 𝑦); 𝑦(0) = 𝑦0
From Taylor’s Expansion;
𝑦𝑖+1 = 𝑦𝑖 + ℎ
𝑑𝑦
𝑑𝑥
+
1
2!
(
𝑑2
𝑦
𝑑𝑥2
) ℎ2
+ 𝑂(ℎ3
)
𝑦𝑖+1 = 𝑦𝑖 + ƒ( 𝑥𝑖, 𝑦𝑖)ℎ +
1
2!
ƒ′( 𝑥𝑖, 𝑦𝑖)ℎ2
+ 𝑂(ℎ3
)
ℎ = 𝑥𝑖+1 − 𝑥𝑖
ƒ′(x, y) =
∂ƒ
∂x
+
𝜕ƒ
𝜕𝑦
𝑑𝑦
𝑑𝑥
So instead to finding derivative of ƒ over and over he assumed the equation to be:
𝑦𝑖+1 = 𝑦𝑖 + ( 𝑎1 𝑘1 + 𝑎2 𝑘2)ℎ
𝑎1 + 𝑎2 = 1; 𝑎2 𝑝1 =
1
2
; 𝑎2 𝑞11 =
1
2
𝑘1 = ƒ( 𝑥𝑖, 𝑦𝑖); 𝑘2 = ƒ(𝑥𝑖 + 𝑝1ℎ, 𝑦𝑖 + 𝑞11 𝑘1ℎ)

20. 20
HEUN’S METHOD:
In this method the value of 𝑎2 was taken as 1/2.
𝑎1 + 𝑎2 = 1 ⇒ 𝑎1 = 1/2.
𝑎2 𝑝1 =
1
2
⇒ 𝑝1 = 1.
𝑎2 𝑞11 =
1
2
⇒ 𝑞11 = 1.
MID-POINT METHOD:
In this method the value of 𝑎2 is assumed as 1.
𝑎1 + 𝑎2 = 1 ⇒ 𝑎1 = 0.
𝑎2 𝑝1 =
1
2
⇒ 𝑝1 = 1/2.
𝑎2 𝑞11 =
1
2
⇒ 𝑞11 = 1/2.
RALSTON’S METHOD:
In this method the value of 𝑎2 was taken to be 2/3.
𝑎1 + 𝑎2 = 1 ⇒ 𝑎1 = 1/3.
𝑎2 𝑝1 =
1
2
⇒ 𝑝1 = 3/4.
𝑎2 𝑞11 =
1
2
⇒ 𝑞11 = 3/4.
Matlab code of all the combined three methods i.e. Heuns, Mid-point, and Ralston’s
Method is:

21. 21
% Solve y'(t)= exp(-2*x)-3*y with y0=5 using all three method
y0 = 5; % Initial Condition
h = 0.5; % step size
x = 0:h:4; % x goes from 0 to 4 seconds
yexact = exp(-3*x).*(exp(x)+4) % Exact solution
y=zeros(size(x)) % Preallocate array
y(1) = y0; % Initial condition gives solution at x=0.
for i=1:(length(x)-1)
k1 = exp(-2*x(i))-3*y(i)
k2 = exp(-2*(x(i)+h))-3*(y(i)+k1*h)
y1(i+1) = y(i)+h*(0.5*k1+0.5*k2) % Approximate solution for next value of y
end
for i=1:(length(x)-1)
m1=exp(-2*x(i))-3*y(i)
m2=exp(-2*(x(i)+(h/2)))-3*(y(i)+m1*(h/2))
y2(i+1)= y(i)+(h*m2) % Approximate solution for next value of y
end
for i=1:(length(x)-1)
n1=exp(-2*x(i))-3*y(i)
n2=exp(-2*(x(i)+(3*h/4)))-3*(y(i)+n1*(3*h/4))
y3(i+1)= y(i)+((1/3)*n1+(2/3)*n2)*h % Approximate solution for next value of y
end
plot(x,yexact,x,y1,x,y2,x,y3);
xlabel('dependent variable x')
title('Heuns+Mid-point+Raltons Methods')
legend('Exact','Heuns','Mid-point','Ralston');
And the result comes out to be:

22. 22
Matlab code and graph for Heun’s Method is:
%% Example
% Solve y'(t)= exp(-2*x)-3*y with y0=5 using Heun's method
y0 = 5; % Initial Condition
h = 0.5; % step size
x = 0:h:4; % x goes from 0 to 4 seconds
yexact = exp(-3*x).*(exp(x)+4) % Exact solution
y=zeros(size(x)) % Preallocate array
y(1) = y0; % Initial condition gives solution at x=0.
for i=1:(length(x)-1)
k1 = exp(-2*x(i))-3*y(i)
k2 = exp(-2*(x(i)+h))-3*(y(i)+k1*h)
y(i+1) = y(i)+h*(0.5*k1+0.5*k2); % Approximate solution for next value of y
end
plot(x,yexact,x,y,x,yexact-y);
xlabel('dependent variable x')
title('Heuns Method')
legend('Exact','Approximate','error');

23. 23
RUNGE-KUTTA 4th
ORDER METHOD:
dy
dx
= ƒ( 𝑥, 𝑦); 𝑦(0) = 𝑦0
From Taylor’s Expansion;
𝑦𝑖+1 = 𝑦𝑖 + ℎ
𝑑𝑦
𝑑𝑥
+
1
2!
(
𝑑2
𝑦
𝑑𝑥2
) ℎ2
+
1
3!
(
𝑑3
𝑦
𝑑𝑥3
) ℎ3
+
1
4!
(
𝑑4
𝑦
𝑑𝑥4
) ℎ4
+ 𝑂(ℎ4
)
𝑦𝑖+1 = 𝑦𝑖 + ƒ( 𝑥𝑖, 𝑦𝑖)ℎ +
1
2!
ƒ′( 𝑥𝑖, 𝑦𝑖)ℎ2
+
1
3!
ƒ′′( 𝑥𝑖, 𝑦𝑖)ℎ3
+
1
4!
ƒ′′′( 𝑥𝑖, 𝑦𝑖)ℎ4
+ 𝑂(ℎ4
)
ℎ = 𝑥𝑖+1 − 𝑥𝑖
ƒ′(x, y) =
∂ƒ
∂x
+
𝜕ƒ
𝜕𝑦
𝑑𝑦
𝑑𝑥
𝑦𝑖+1 = 𝑦𝑖 + ( 𝑎1 𝑘1 + 𝑎2 𝑘2 + 𝑎3 𝑘3 + 𝑎4 𝑘4)ℎ
RK4 METHOD BY RUNGE:
He assumed the value of the variable as:
𝑦𝑖+1 = 𝑦𝑖 +
1
6
( 𝑘1 + 2𝑘2 + 2𝑘3 + 𝑘4)ℎ
𝑘1 = ƒ( 𝑥𝑖, 𝑦𝑖);
𝑘2 = ƒ(𝑥𝑖 +
1
2
ℎ, 𝑦1 +
1
2
𝑘1ℎ)
𝑘3 = ƒ(𝑥𝑖 +
1
2
ℎ, 𝑦𝑖 +
1
2
𝑘2ℎ)
𝑘4 = ƒ(𝑥𝑖 + ℎ, 𝑦𝑖 + 𝑘3ℎ)

24. 24
Matlab code and graph for RK4 Method is:
% Solve y'(t)= exp(-2*x)-3*y with y0=5 using RK4'S method
y0 = 5; % Initial Condition
h = 0.5; % step size
x = 0:h:4; % x goes from 0 to 4 seconds
yexact = exp(-3*x).*(exp(x)+4) % Exact solution
y=zeros(size(x)) % Preallocate array
y(1) = y0; % Initial condition gives solution at x=0.
for i=1:(length(x)-1)
k1 = exp(-2*x(i))-3*y(i)
k2 = exp(-2*(x(i)+0.5*h))-3*(y(i)+0.5*k1*h)
k3 = exp(-2*(x(i)+0.5*h))-3*(y(i)+0.5*k2*h)
k4 = exp(-2*(x(i)+h))-3*(y(i)+k3*h)
y(i+1) = y(i)+(h/6)*(k1+2*k2+2*k3+k4); % Approximate solution for next value of y
end
plot(x,yexact,x,y,x,yexact-y);
xlabel('dependent variable x')
title('RK4 Method')
legend('Exact','RK4_Method','error');

25. 25
KUTTA’S METHOD:
𝑦𝑖+1 = 𝑦𝑖 +
1
8
( 𝑘1 + 3𝑘2 + 3𝑘3 + 𝑘4)ℎ
𝑘1 = ƒ( 𝑥𝑖, 𝑦𝑖);
𝑘2 = ƒ(𝑥𝑖 +
1
3
ℎ, 𝑦1 +
1
3
𝑘1ℎ)
𝑘3 = ƒ(𝑥𝑖 +
2
3
ℎ, 𝑦𝑖 −
1
3
ℎ𝑘1 + 𝑘2ℎ)
𝑘4 = ƒ(𝑥𝑖 + ℎ, 𝑦𝑖 + 𝑘1ℎ − 𝑘2ℎ + 𝑘3ℎ)
Matlab code for Kutta’s method.
% Solve y'(t)= exp(-2*x)-3*y with y0=5 using Kutta'S method
y0 = 5; % Initial Condition
h = 0.5; % step size
x = 0:h:4; % x goes from 0 to 4 seconds
yexact = exp(-3*x).*(exp(x)+4) % Exact solution
y=zeros(size(x)) % Preallocate array
y(1) = y0; % Initial condition gives solution at x=0.
for i=1:(length(x)-1)
k1 = exp(-2*x(i))-3*y(i)
k2 = exp(-2*(x(i)+(1/3)*h))-3*(y(i)+(1/3)*k1*h)
k3 = exp(-2*(x(i)+(2/3)*h))-3*(y(i)-(1/3)*h*k1+k2*h)
k4 = exp(-2*(x(i)+h))-3*(y(i)+h*k1-h*k2+h*k3)
y(i+1) = y(i)+(h/8)*(k1+3*k2+3*k3+k4); % Approximate solution for next value of y
end
plot(x,yexact,x,y,x,yexact-y);
xlabel('dependent variable x')
title('Kutta Method')
legend('Exact','KUTTA Method','error');

26. 26
MULTISTEP METHOD’S
We use linear multistep step methods to find the numerical solution of ordinary
differential equations.
The general form for linear m-step multistep method is
𝑤𝑖+1 − 𝑎2 𝑤𝑖 − 𝑎2 𝑤𝑖−1 − ⋯ − 𝑎 𝑚 𝑤𝑖+1−𝑚
ℎ𝑖
= 𝑏0ƒ( 𝑡𝑖+1, 𝑤𝑖+1) + 𝑏1ƒ( 𝑡𝑖, 𝑤𝑖) + 𝑏2ƒ( 𝑡𝑖−1, 𝑤𝑖−1) + ⋯
+ 𝑏 𝑚ƒ(𝑡𝑖+1−𝑚, 𝑤𝑖+1−𝑚)
When𝑏0 = 0, the method is said to be explicit; otherwise it is said to be implicit.
ADAMS-BASHFORTH METHODS:
This are explicit methods.
The given differential equation is:
𝑦′
(𝑡) = ƒ(𝑡, 𝑦( 𝑡))
Integrating the above differential equation on both sides from t=𝑡𝑖 to t=𝑡𝑖+1. This
gives us an equation of the form of:
𝑦( 𝑡𝑖+1) − 𝑦( 𝑡𝑖) = ∫ ƒ(𝑡, 𝑦( 𝑡))𝑑𝑡.
𝑡 𝑖+1
𝑡 𝑖
Next, we write ƒ(𝑡, 𝑦( 𝑡)) = 𝑃 𝑚−1( 𝑡) + 𝑅 𝑚−1( 𝑡),
𝑃 𝑚−1( 𝑡) = ∑ 𝐿 𝑚−1,𝑗
𝑚
𝑗=1
(𝑡)ƒ(𝑡𝑖+1−𝑗, 𝑦(𝑡𝑖+1−𝑗))
Is the Lagrange form of the polynomial of degree at most m-1 that interpolates ƒ at
the m points 𝑡𝑖, 𝑡𝑖−1, 𝑡𝑖−2, … , 𝑡𝑖+1−𝑚 and

27. 27
𝑅 𝑚−1( 𝑡) =
ƒ(𝑚)
(𝜉, 𝑦( 𝜉))
𝑚!
∏(𝑡 − 𝑡𝑖+1−𝑗
𝑚
𝑗=1
)
Is the corresponding remainder term.
For deriving the 2-step Adams-Bashforth method we take m=2 and for 3-step we
take m=3 and so on.
The two-step Adams-Bashforth method is:
𝑤𝑖+1 − 𝑤𝑖
ℎ
=
3
2
ƒ( 𝑡𝑖, 𝑤𝑖) −
1
2
ƒ(𝑡𝑖−1, 𝑤𝑖−1)
With local truncation error
𝜏𝑖 =
5ℎ2
12
𝑦′′′( 𝜉) = 𝑂(ℎ2).
And the three-step Adams-Bashforth method is:
𝑤𝑖+1 − 𝑤𝑖
ℎ
=
23
12
ƒ( 𝑡𝑖, 𝑤𝑖) −
4
3
ƒ( 𝑡𝑖−1, 𝑤𝑖−1) +
5
12
ƒ( 𝑡𝑖−2, 𝑤𝑖−2)
𝜏𝑖 =
3ℎ3
8
𝑦′′′′( 𝜉) = 𝑂(ℎ3).
Matlab code for two-step Adams-Bashforth method is:
%% Example
% Solve y'(x)=exp(-2*x)-3*y with y0=5 using 2-step Adams Bashforth's approach
y0=5; % Initial Condition
h = 0.5; % Step size
x = 0:h:6; % x goes from 0 to 6.
yexact = exp(-3*x).*(exp(x)+5) % Exact solution
y=zeros(size(x)) % Preallocate array
y(1)=y0 % Initial condition gives solution at
x=0.
for i=1:(length(x)-2) % Using for loop
y(i+2)= y(i+1)+(h)*((1.5)*exp(-2*x(i+1)-3*y(i+1))-(0.5)*exp((-2*x(i))-3*y(i)))
% Approximate solution for next value of y
end
plot(x,yexact,x,y,x,yexact-y);
xlabel('dependent variable x')
title('Adams Bashforths 2-step method')
legend('Exact','Approximate','error');

28. 28
The result is:
And for three-step Adams-Bashforth method is:
%% Example
% Solve y'(x)=exp(-2*x)-3*y with y0=5 using 3-step Adams Bashforth's approach
y0=5; % Initial Condition
h = 0.5; % Step size
x = 0:h:6; % x goes from 0 to 6.
yexact = exp(-3*x).*(exp(x)+5) % Exact solution
y=zeros(size(x)) % Preallocate array
y(1)=y0 % Initial condition gives solution at
x=0.
for i=1:(length(x)-2) % Using for loop
y(i+2)= y(i+1)+(h)*((23/12)*exp(-2*x(i+2)-3*y(i+2))-(4/3)*exp((-2*x(i+1))-
3*y(i+1))+(5/12)*exp((-2*x(i))-3*y(i))) % Approximate solution for next value of y
end
plot(x,yexact,x,y,x,yexact-y);
xlabel('dependent variable x')
title('Adams Bashforths 3-step method')
legend('Exact','Approximate','error');

29. 29
ADAMS-MOULTON METHODS:
This method is different from Adams-Bashforth method in the sense that instead of
interpolating ƒ at𝑡𝑖, 𝑡𝑖−1, 𝑡𝑖−2, … , 𝑎𝑛𝑑 𝑡𝑖+1−𝑚, we also interpolate at 𝑡𝑖+1.
The Two-step Adams-Moulton method is:
𝑤𝑖+1 − 𝑤𝑖
ℎ
=
5
12
ƒ( 𝑡𝑖+1, 𝑤𝑖+1) +
2
3
ƒ(𝑡𝑖, 𝑤𝑖) −
1
12
ƒ(𝑡𝑖−1, 𝑤𝑖−1)
With local truncation error
𝜏𝑖 = −
ℎ3
24
𝑦′′′′( 𝜉) = 𝑂(ℎ3).

30. 30
The three-step Adams-Moulton method is given by the difference equation:
𝑤𝑖+1 − 𝑤𝑖
ℎ
=
9
24
ƒ( 𝑡𝑖+1, 𝑤𝑖+1) +
19
24
ƒ( 𝑡𝑖, 𝑤𝑖) −
5
24
ƒ( 𝑡𝑖−1, 𝑤𝑖−1) +
1
24
ƒ( 𝑡𝑖−2, 𝑤𝑖−2),
With local truncation error
𝜏𝑖 = −
19ℎ4
720
𝑦(5)( 𝜉) = 𝑂(ℎ4).
Matlab code for two-step and three-step Adams-Moulton method is:
%% Example
% Solve y'(x)=exp(-2*x)-3*y with y0=5 using 2-step and 3-step Adams Moulton's approach
y0=5; % Initial Condition
h = 0.5; % Step size
x = 0:h:6; % x goes from 0 to 6.
yexact = exp(-3*x).*(exp(x)+5) % Exact solution
y=zeros(size(x)) % Preallocate array
y1=zeros(size(x)) % Preallocate array
y(1)=y0 % Initial condition gives solution at
x=0.
for i=1:(length(x)-3) % Using for loop
y(i+2)= y(i+1)+(h)*((5/12)*exp(-2*x(i+2)-3*y(i+2))+(2/3)*exp((-2*x(i+1))-
3*y(i+1))+(1/12)*exp((-2*x(i))-3*y(i))) % Approximate solution for next value of y for 2-
step
y1(i+2)= y(i+1)+(h)*((9/24)*exp(-2*x(i+3)-3*y(i+3))+(19/24)*exp((-2*x(i+2))-
3*y(i+2))-(5/24)*exp((-2*x(i+1))-3*y(i+1))+(1/24)*exp((-2*x(i))-3*y(i))) % Approximate
solution for next value of y for 3-step
end
plot(x,yexact,x,y,x,y1);
xlabel('dependent variable x')
title('Adams Moultons 2-step and 3-step method')
legend('Exact','2-step','3-step');

31. 31
And the resulting analysis is:

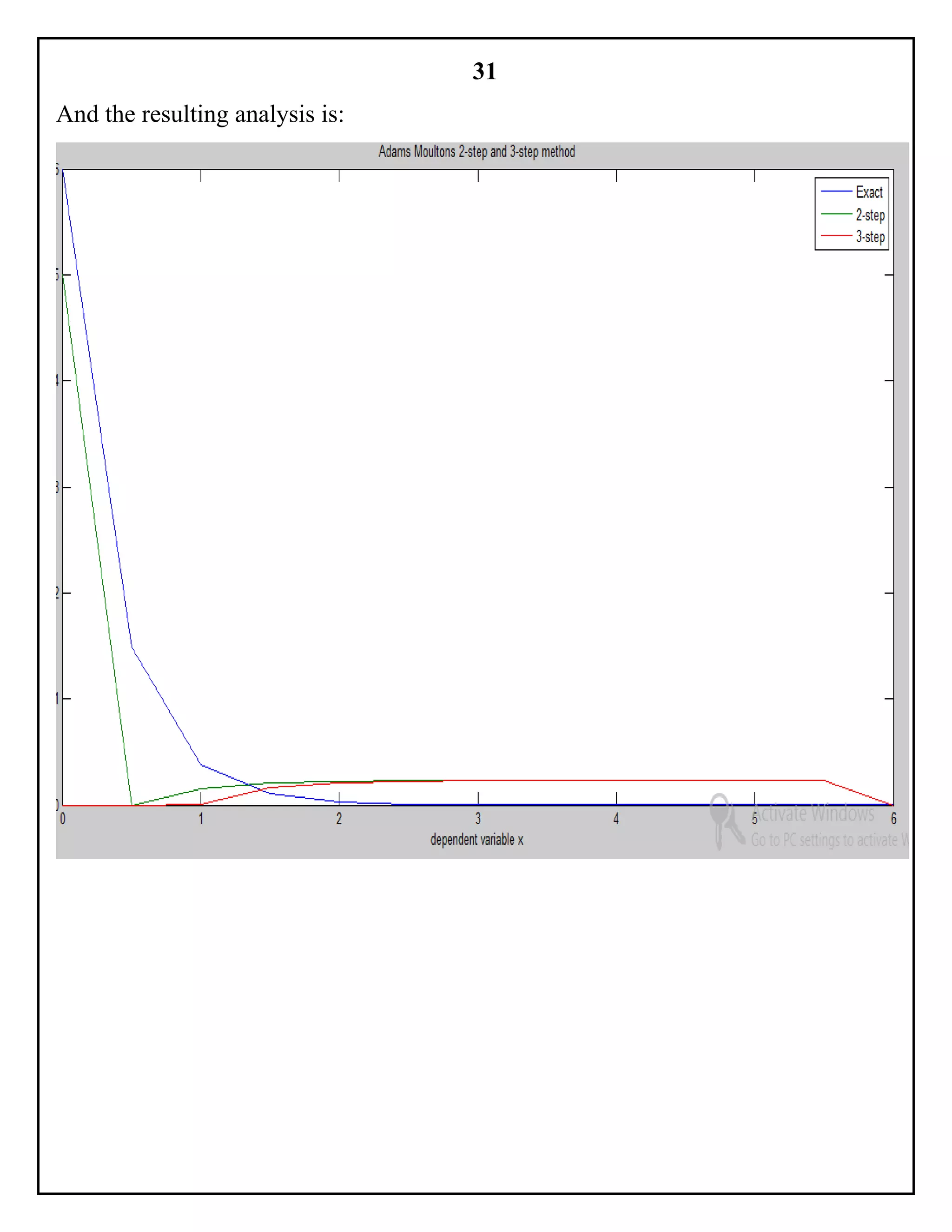
32. 32
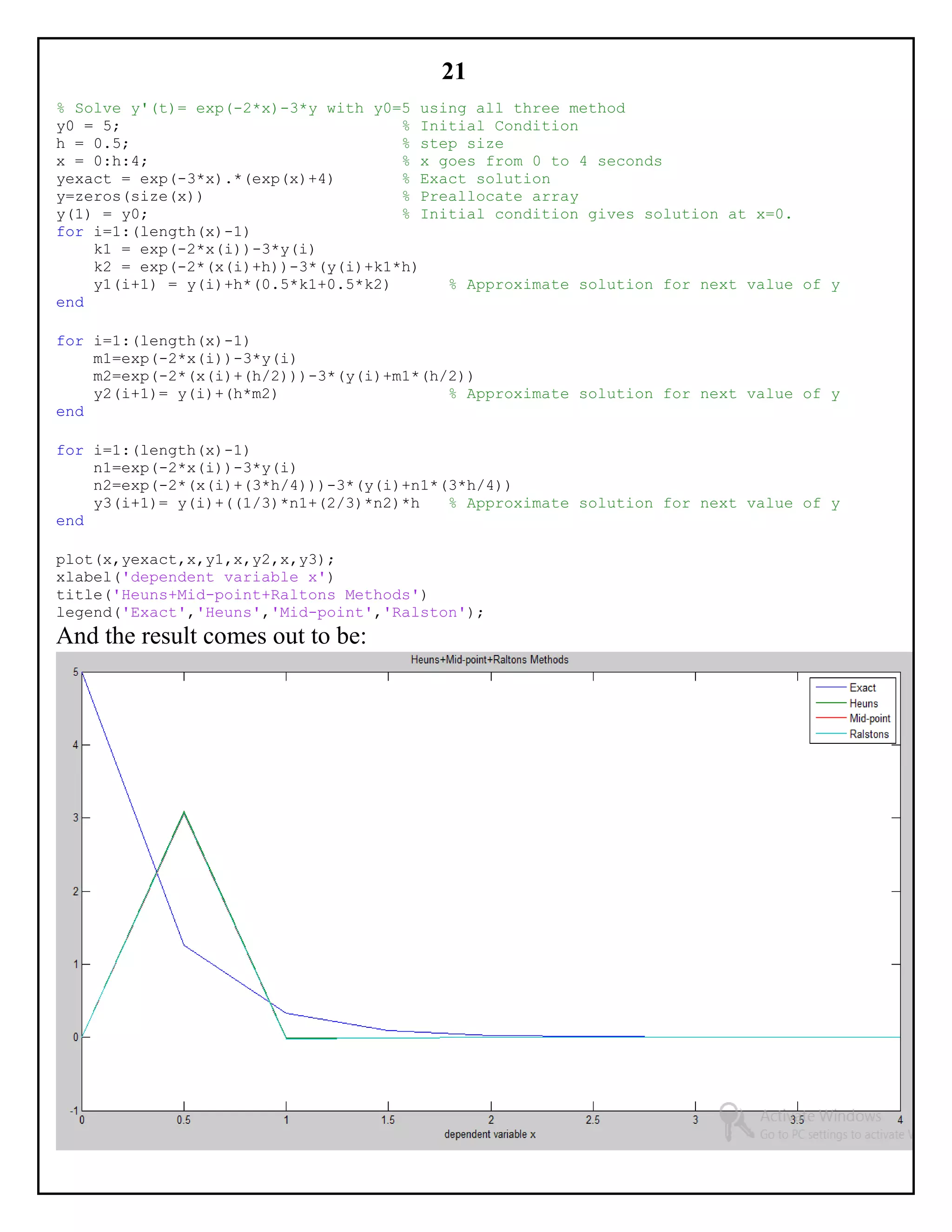
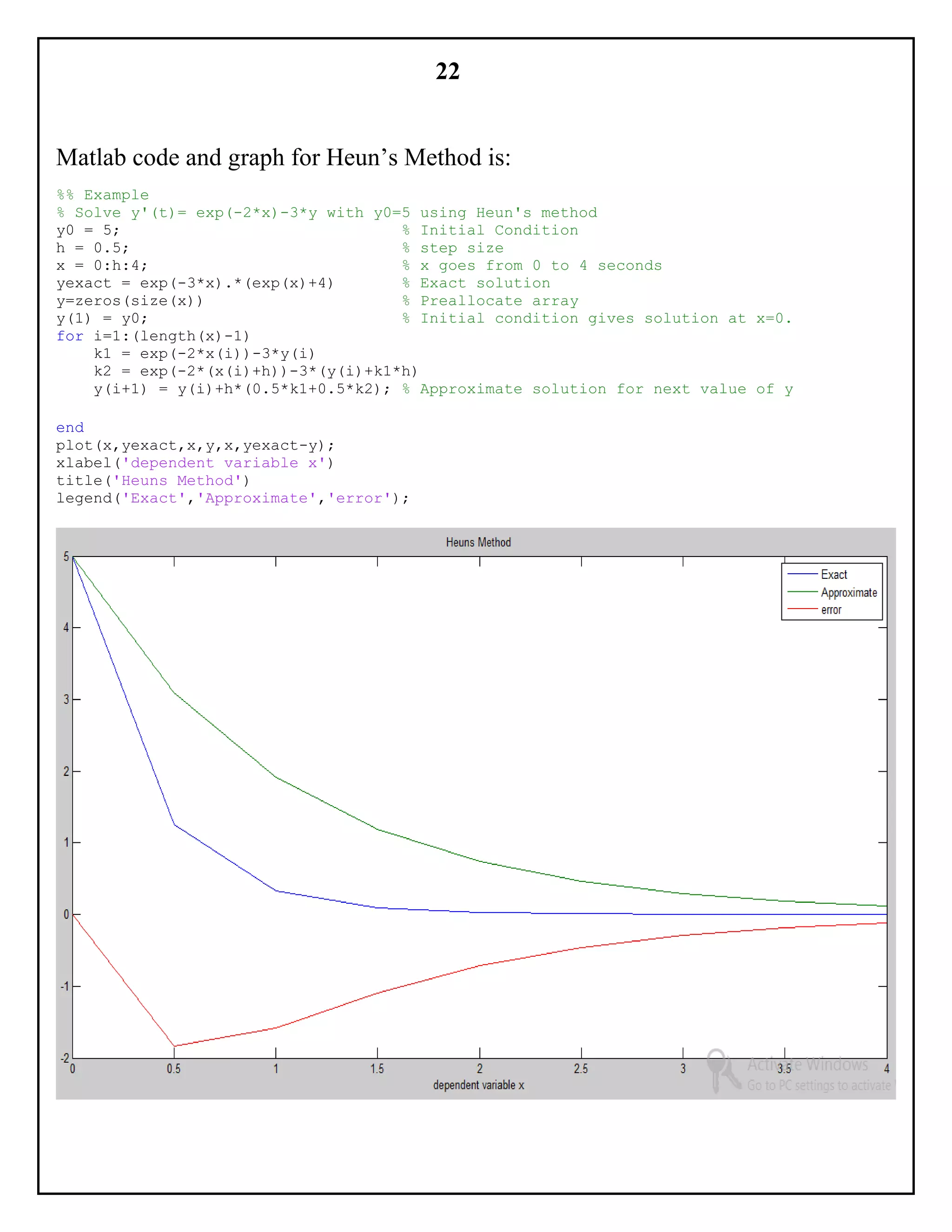
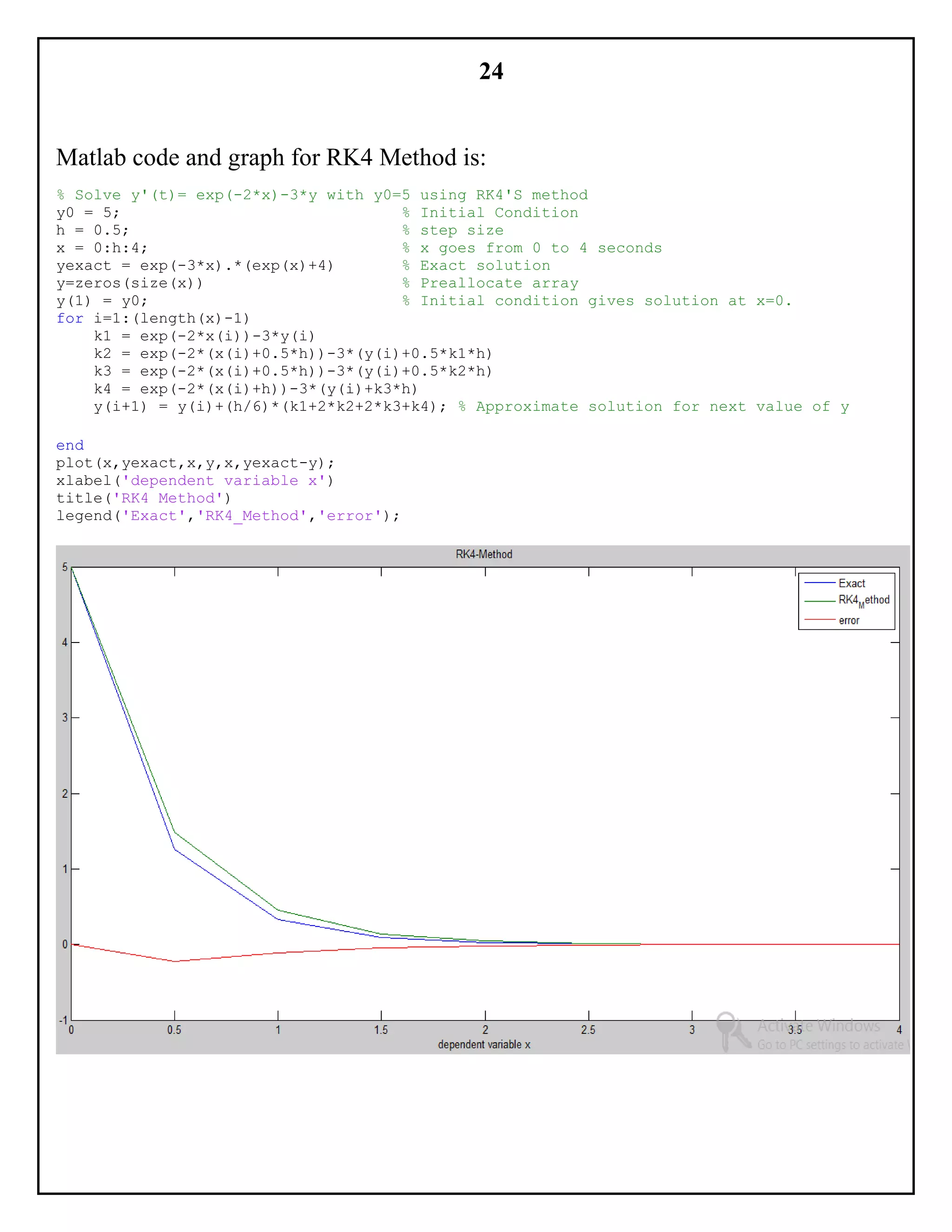
PREDICTOR COLLECTOR METHODS:
It is one of the method for calculating numerical solution of differential equation
with a given initial value. This solution is a curve g(x, y) in (x, y) plane, whose
slope at every point (x, y) in the specified region is given by the equation
dy
dx
= ƒ(𝑥, 𝑦).
This method uses an explicit method to “predict” an approximate value, 𝑊𝑖+1, and
then to “correct” 𝑊𝑖+1 to 𝑤𝑖+1 with the equation of the implicit method. This is the
basic idea behind a predictor-corrector scheme.
The most popular of the predictor-collector schemes is the Adams fourth order
predictor-collector method. This uses four-step, four-order Adams-Bashforth
method:
𝑊𝑖+1 − 𝑤𝑖
ℎ
=
1
24
[55ƒ( 𝑡𝑖, 𝑤𝑖) − 59ƒ( 𝑡𝑖−1, 𝑤𝑖−1) + 37ƒ( 𝑡𝑖−2, 𝑤𝑖−2) − 9ƒ( 𝑡𝑖−3, 𝑤𝑖−3)]
As a predictor, followed by three step, fourth order Adams-Moulton method
𝑤𝑖+1 − 𝑤𝑖
ℎ
=
1
24
[9ƒ( 𝑡𝑖+1, 𝑊𝑖+1) + 19ƒ( 𝑡𝑖, 𝑤𝑖) − 5ƒ( 𝑡𝑖−1, 𝑤𝑖−1) + ƒ( 𝑡𝑖−2, 𝑤𝑖−2)]
As a collector.
This scheme requires only two new functions evaluations, ƒ(𝑡𝑖, 𝑤𝑖) and
ƒ(𝑡𝑖+1, 𝑊𝑖+1), per time step. The required starting values (𝑤1, 𝑤2, 𝑤3) are typically
obtained from the classical fourth-order Runge-Kutta method.

33. 33
CONVERGENCE AND STABILITY FOR MODIFIED AND EULER
METHOD.
For the modified Euler method
Φ (ƒ, 𝑡𝑖, 𝑦, ℎ) = ƒ (𝑡𝑖 +
ℎ
2
, 𝑦 +
ℎ
2
ƒ( 𝑡𝑖, 𝑦)).
If ƒ satisfies Lipschitz condition in y on the set D = {(t, y) |a≤t≤b, y∈ R} with
Lipschitz constant L. Then
|Φ (ƒ, 𝑡𝑖, 𝑦1, ℎ)- Φ (ƒ, 𝑡𝑖, 𝑦2, ℎ)|=| ƒ (𝑡 +
ℎ
2
, 𝑦1 +
ℎ
2
ƒ( 𝑡, 𝑦1))-ƒ (𝑡 +
ℎ
2
, 𝑦2 +
ℎ
2
ƒ( 𝑡, 𝑦2))| ≤ L|𝑦1 +
ℎ
2
ƒ( 𝑡, 𝑦1) − 𝑦2 −
ℎ
2
ƒ( 𝑡, 𝑦2)|
≤ L|𝑦1 − 𝑦2| +
ℎ𝐿
2
|ƒ( 𝑡, 𝑦1) −
ℎ
2
ƒ( 𝑡, 𝑦2)|
≤L|𝑦1 − 𝑦2| +
ℎ𝐿2
2
|𝑦1 − 𝑦2|=(L+h
𝐿2
2
)|𝑦1 − 𝑦2|.
Therefore ϕ satisfies a Lipschitz condition in y on the set
{(ƒ,t,y,h)|ƒ(t,y) is Lipschitz in y on D, (t,y) ∈ D, 0≤h≤ℎ0}
For any ℎ0 > 0 with Lipschitz constant
𝐿 𝜙 = 𝐿 +
ℎ0 𝐿2
2
.
Hence we may conclude that the modified Euler method is stable.
Consistency of Modified Euler Method.
The difference equation for the modified Euler Method is:
𝑤𝑖+1 − 𝑤𝑖
ℎ
= ƒ (𝑡𝑖 +
ℎ
2
, 𝑤𝑖 +
ℎ
2
ƒ( 𝑡𝑖, 𝑤𝑖)) ;
Hence,
Φ (ƒ, 𝑡𝑖, 𝑤𝑖, ℎ) = ƒ (𝑡𝑖 +
ℎ
2
, 𝑤𝑖 +
ℎ
2
ƒ( 𝑡𝑖, 𝑤𝑖)).

34. 34
It then follows that
Φ (ƒ, 𝑡𝑖, 𝑦, 0) = ƒ (𝑡𝑖 +
0
2
, 𝑦𝑖 +
0
2
ƒ( 𝑡𝑖, 𝑦𝑖))= ƒ( 𝑡𝑖, 𝑤𝑖)
So the modified Euler method is consistent.
LINEAR MULTISTEP METHODS
The general form for linear m-step multistep method is
𝑤 𝑖+1−𝑎2 𝑤𝑖−𝑎2 𝑤 𝑖−1−⋯−𝑎 𝑚 𝑤 𝑖+1−𝑚
ℎ 𝑖
= 𝑏0ƒ( 𝑡𝑖+1, 𝑤𝑖+1) + 𝑏1ƒ( 𝑡𝑖, 𝑤𝑖) + 𝑏2ƒ( 𝑡𝑖−1, 𝑤𝑖−1) +
⋯ + 𝑏 𝑚ƒ(𝑡𝑖+1−𝑚, 𝑤𝑖+1−𝑚). – (2)
For (2) to be consistent, we must have 𝜏𝑖→0 as h→0. This requires that the local
truncation error be at least O(h); that is, the method must be at least first order, the
coefficient 𝑎𝑗 𝑎𝑛𝑑 𝑏𝑗 must satisfy
∑ 𝑎𝑗 = 1
𝑚
𝑗=1
𝑎𝑛𝑑 ∑ 𝑎𝑗( 𝑚 − 𝑗) + ∑ 𝑏𝑗 = 𝑚
𝑚
𝑗=0
𝑚
𝑗=1
For the method to be at least first order. The consistency condition for linear
multistep methods are given by
∑ 𝑎𝑗 = 1
𝑚
𝑗=1
𝑎𝑛𝑑 − ∑ 𝑗𝑎𝑗 + ∑ 𝑏𝑗 = 0
𝑚
𝑗=0
𝑚
𝑗=1

35. 35
CONCLUSION
The main goal of the project is to find approximate solutions of Ordinary
Differential Equation with a given initial value by using different
techniques/methods of Numerical Analysis especially for multistep methods. In this
project I analyzed the variation of error of the approximated solution from the true
solution for both one-step and multistep methods. I used Matlab software for the
simulation purposes. Various methods like Runge-Kutta, Euler, Adams-Bashforth,
Adams-Moulton, etc. were investigated for finding the approximated solution, and
the methods were being simulated in Matlab Software. The stability, Convergence
and Consistent of Modified Euler method were also being investigated.

36. 36
BIBLIOGRAPHY
1- A friendly introduction to numerical analysis by Brian Bradie.
2- Numerical Analysis by Richard L. Burden and J. Douglas Faires.
3- Differential Equations by Shepley L. Ross.
4- Elementary Numerical Analysis by Kendall Atkinson Weiminhan.
5- https://en.wikipedia.org/wiki/Numerical_analysis
6- https://en.wikipedia.org/wiki/Linear_multistep_method
7- NPTEL video lectures
https://www.youtube.com/watch?v=88ys5ZIolSg&list=PL87971F342396DB2
B
https://www.youtube.com/watch?v=QQFIWwDA9NM
8- http://mathforcollege.com/nm/videos/youtube/08ode/rungekutta2nd/rungekutt
a2nd_08ode_background.html