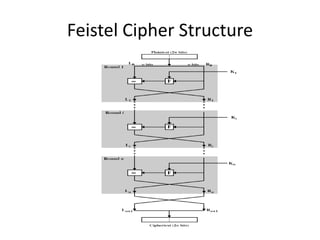
The document discusses encryption techniques, primarily focusing on the one-time pad, which is provably secure when used correctly with a random key only known to the sender and receiver. It also covers historical cryptographic methods like the Zimmerman telegram and introduces modern block ciphers, particularly the Feistel cipher structure, which allows for secure and efficient decryption. Additionally, it highlights Claude Shannon's foundational contributions to information theory and cipher design.

1. One-time Pad: Encryption
e=000 h=001 i=010 k=011 l=100 r=101 s=110 t=111
h e i l h i t l e r
001 000 010 100 001 010 111 100 000 101
111 101 110 101 111 100 000 101 110 000
110 101 100 001 110 110 111 001 110 101
s r l h s s t h s r
Encryption: Plaintext  Key = Ciphertext
Plaintext:
Key:
Ciphertext:

2. One-time Pad: Decryption
e=000 h=001 i=010 k=011 l=100 r=101 s=110 t=111
s r l h s s t h s r
110 101 100 001 110 110 111 001 110 101
111 101 110 101 111 100 000 101 110 000
001 000 010 100 001 010 111 100 000 101
h e i l h i t l e r
Decryption: Ciphertext  Key = Plaintext
Ciphertext:
Key:
Plaintext:

3. One-time Pad
e=000 h=001 i=010 k=011 l=100 r=101 s=110 t=111
s r l h s s t h s r
110 101 100 001 110 110 111 001 110 101
101 111 000 101 111 100 000 101 110 000
011 010 100 100 001 010 111 100 000 101
k i l l h i t l e r
Ciphertext:
“key”:
“Plaintext”:
Double agent claims sender used following “key”

4. One-time Pad
e=000 h=001 i=010 k=011 l=100 r=101 s=110 t=111
s r l h s s t h s r
110 101 100 001 110 110 111 001 110 101
111 101 000 011 101 110 001 011 101 101
001 000 100 010 011 000 110 010 011 000
h e l i k e s i k e
Ciphertext:
“Key”:
“Plaintext”:
Or sender is captured and claims the key is…

5. One-time Pad Summary
• Provably secure…
– Ciphertext provides no info about plaintext
– All plaintexts are equally likely
• …but, only when be used correctly
– Pad must be random, used only once
– Pad is known only to sender and receiver
• Note: pad (key) is same size as message
• So, why not distribute msg instead of pad?

6. Codebook Cipher
• Literally, a book filled with “codewords”
• Zimmerman Telegram encrypted via codebook
Februar 13605
fest 13732
finanzielle 13850
folgender 13918
Frieden 17142
Friedenschluss 17149
: :
• Modern block ciphers are codebooks!
• More about this later…

7. Codebook Cipher: Additive
• In practice, also used additive
• Additive  book of “random” numbers
– Sender encrypts msg with codebook
– Then chooses position in additive book
– Adds additive numbers to get ciphertext
– Send ciphertext and additive position (MI)
– Recipient subtracts additives before decrypting
• Why use an additive sequence?

8. Zimmerman
Telegram
• Perhaps most
famous codebook
ciphertext ever
• A major factor in
U.S. entry into WWI

9. Zimmerman
Telegram
Decrypted
 British had
recovered partial
codebook
 Then able to fill in
missing parts

10. Post-WWII History
• Claude Shannon  father of the science of
information theory
• Computer revolution  lots of data to protect
• Data Encryption Standard (DES), 70’s
• Public Key cryptography, 70’s
• CRYPTO conferences, 80’s
• Advanced Encryption Standard (AES), 90’s
• The crypto genie is out of the bottle…

11. Claude Shannon
• The founder of Information Theory
• 1949 paper: Comm. Thy. of Secrecy Systems
• Fundamental concepts
– Confusion  obscure relationship between plaintext
and ciphertext, substitution ciphers
– Diffusion  spread plaintext statistics through the
ciphertext, transposition ciphers
• Proved one-time pad is secure
• One-time pad is confusion-only, while transposition
is diffusion-only

12. Steganography
• an alternative to encryption
• hides existence of message
– using only a subset of letters/words in a longer
message marked in some way
– using invisible ink
– hiding in LSB in graphic image or sound file
• has drawbacks
– high overhead to hide relatively few info bits

13. Modern Block Ciphers
• will now look at modern block ciphers
• one of the most widely used types of
cryptographic algorithms
• provide secrecy and/or authentication
services
• in particular will introduce DES (Data
Encryption Standard)

14. Stream Cipher
 There is a plain text stream
 P = P1P2P3. . .
 There is a cipher text stream
 C = C1C2C3. . .
 There is a key stream
 K = (k1, k2, k3, . . . )

15. Stream Cipher

16. Stream cipher
 Examples
 Additive cipher
 K = (k, k, k, . . . )
 Monoalphabetic substitution cipher
 K = mapping of the current PT char to CT char,
. . .
 Vigenere cipher
 K = (k1, k2, . . . , km, k1, k2, . . .)

17. Block cipher

18. Block cipher
 Examples
 Play fair cipher (block size = 2)
 DES, AES

19. Block Cipher Principles
• most symmetric block ciphers are based on a Feistel
Cipher Structure
• needed since must be able to decrypt ciphertext to
recover messages efficiently
• block ciphers look like an extremely large
substitution
• would need table of 264 entries for a 64-bit block
• instead create from smaller building blocks
• using idea of a product cipher

20. Claude Shannon and Substitution-
Permutation Ciphers
• in 1949 Claude Shannon introduced idea of
substitution-permutation (S-P) networks
– modern substitution-transposition product cipher
• these form the basis of modern block ciphers
• S-P networks are based on the two primitive
cryptographic operations we have seen before:
– substitution (S-box)
– permutation (P-box)
• provide confusion and diffusion of message

21. Feistel Cipher Structure
• Horst Feistel devised the feistel cipher
– based on concept of invertible product cipher
• partitions input block into two halves
– process through multiple rounds which
– perform a substitution on left data half
– based on round function of right half & subkey
– then have permutation swapping halves
• implements Shannon’s substitution-
permutation network concept

22. Feistel Cipher Structure

23. Feistel Cipher Design Principles
• block size
– increasing size improves security, but slows cipher
• key size
– increasing size improves security, makes exhaustive key searching
harder, but may slow cipher
• number of rounds
– increasing number improves security, but slows cipher
• subkey generation
– greater complexity can make analysis harder, but slows cipher
• round function
– greater complexity can make analysis harder, but slows cipher
• fast software en/decryption & ease of analysis
– are more recent concerns for practical use and testing

24. Feistel Cipher: Encryption
• Feistel cipher is a type of block cipher design, not a
specific cipher
• Split plaintext block into left and right halves: P =
(L0,R0)
• For each round i = 1,2,...,n, compute
Li= Ri1
Ri= Li1  F(Ri1,Ki)
where F is round function and Ki is subkey
• Ciphertext: C = (Ln,Rn)

25. Feistel Cipher: Decryption
• Start with ciphertext C = (Ln,Rn)
• For each round i = n,n1,…,1, compute
Ri1 = Li
Li1 = Ri  F(Ri1,Ki)
where F is round function and Ki is subkey
• Plaintext: P = (L0,R0)
• Formula “works” for any function F
– But only secure for certain functions F

26. Feistel Cipher Decryption