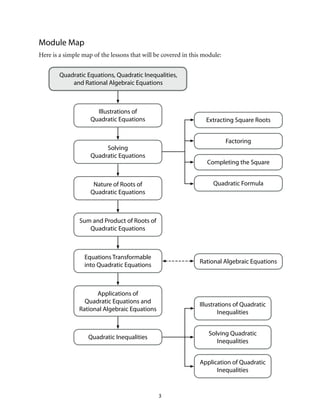
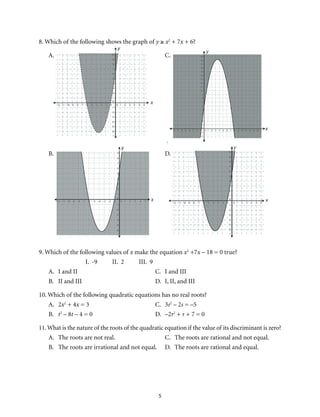
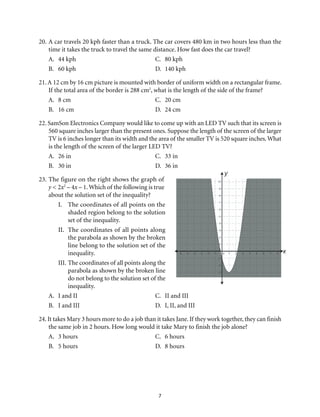
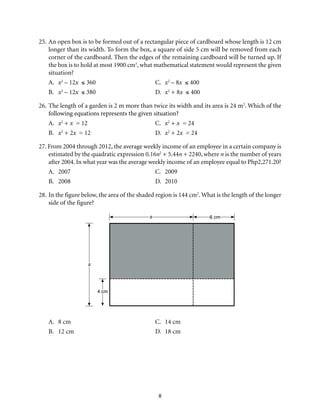
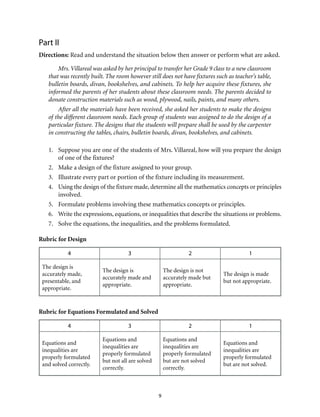
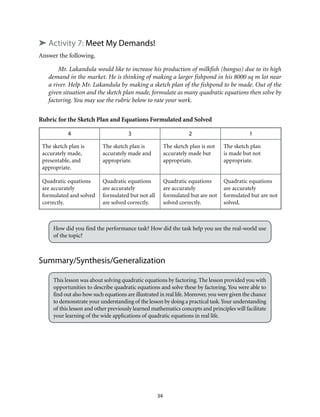
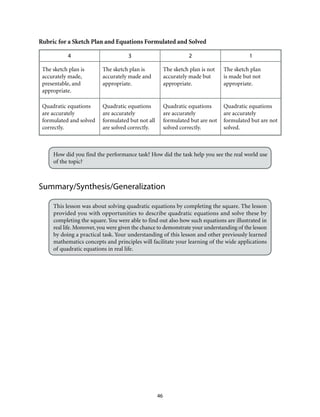
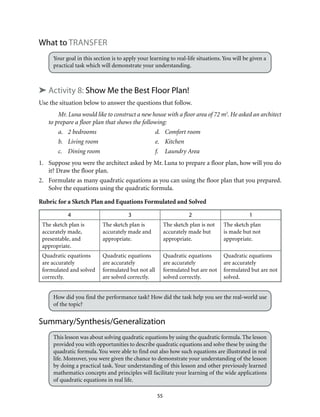
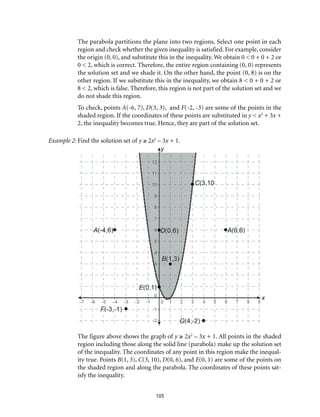
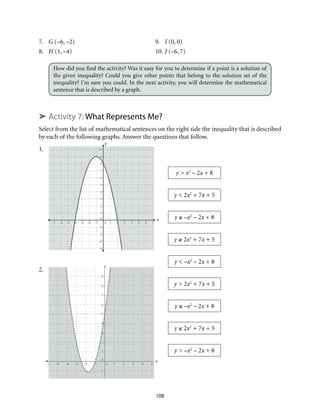
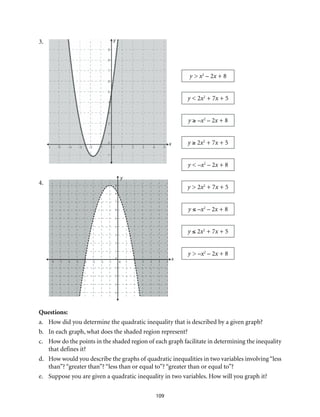
This document provides an introduction to Module 1 of a mathematics learner's material on quadratic equations and inequalities. It includes 7 objectives that will be covered across 7 lessons. Lesson 1 will illustrate quadratic equations, Lesson 2 will cover solving quadratic equations using extracting square roots, factoring, completing the square, and the quadratic formula. Lesson 3 will discuss the nature of roots of quadratic equations. Lesson 4 will describe the relationship between coefficients and roots. Lesson 5 will solve equations transformable into quadratic equations. Lesson 6 will apply quadratic equations to problems. Lesson 7 will illustrate and solve quadratic inequalities and problems involving them. The document provides the structure and overview of the topics to be discussed in the module.