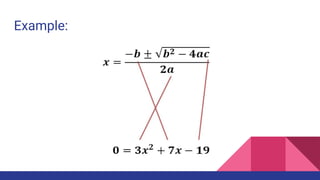
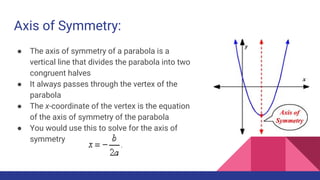
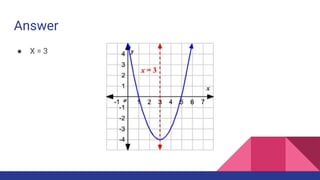
This document provides an overview of key concepts related to quadratic equations including: the quadratic formula for solving quadratic equations, properties of parabolas including their vertex and axis of symmetry, using factoring and graphs to find zeros of quadratic functions, and examples of parabolas in real life such as rainbows and bridges. Key topics covered include the standard and vertex forms of quadratic equations, finding maximums and minimums, and using the quadratic formula. Real-world applications and examples are provided throughout.

1. Quadratics:
Made by: Zachary Ray
Angel Ortiz
Cameron Taylor

2. What we will learn:
● Quadratic Equation
● Quadratic Formula
● Parabola (Maximum/Minimum)
● Standard Form
● Vertex/Vertex form
● Axis of Symmetry
● Zero of a function
● Root of an equation

3. Quadratic Equation:
●
● Quadratic Equations make curves called parabolas, like this one:
Quadratic Equation:

4. Quadratic Formula:
● Method for solving quadratic equations
● You would first get the a, b, and c and then
you would plug it into the formula
● Then solve for X

5. Example:

6. Real Life Examples of Parabolas:
Rainbows
St. Louis Arch

7. Real Life Examples of Parabolas:

8. Real Life Examples of Parabolas:

9. Parabolas Maximum and Minimum:
● A maximum parabola would open downward
● A minimum parabola would open upward
● A parabola opening downward looks like
a sad face
● A parabola opening upward looks like a smiley face

10. Standard Form:
Standard Form of an equation:
● a, b and c are known values
● a can’t be 0
● a, b and c are the coefficients of the equation

11. Vertex/Vertex Form:
● Vertex is the point where the curve transforms its path
● Vertex Form: y = a(x - h)2
+ k
● (h,k) is the vertex in the parabola
● If a is positive then the parabola opens upwards like a regular "U"
● If a is negative, then the graph opens downwards like an upside down "U"

12. Axis of Symmetry:
● The axis of symmetry of a parabola is a
vertical line that divides the parabola into two
congruent halves
● It always passes through the vertex of the
parabola
● The x-coordinate of the vertex is the equation
of the axis of symmetry of the parabola
● You would use this to solve for the axis of
symmetry

13. Example:
● Find the axis of symmetry of the graph of y = x2
– 6 x + 5
● Use
● Here, a = 1, b = –6, and c = 5

14. Answer
● X = 3

15. Zero of a Function:
● The zero of a function is the x-value that makes the function equal to 0
● There are different ways to solve for a zero
● One of them is by using a graph and table
● Another way is by factoring

16. Graph and a table: Example
● Find the zeros of g(x) = −x2−2x+3 by using graph and table

17. Answer:
The vertex is (-1,4)

18. Zero of a Function: Factoring
● Solve x2−4x−12 by factoring

19. Answer:
● x = -2 or x = 6

20. Works Cited:
● https://www.mathsisfun.com/algebra/quadratic-equation.html
● http://pixshark.com/quadratic-function-examples-in-real-life.htm
● http://www.thinglink.com/scene/508444480022511616
● https://sites.google.com/a/warrenk12nc.org/integrated-math-iii/all-
units/unit-4/find-zeros-vertex-minimum-maximum
● http://formulas.tutorvista.com/math/vertex-formula.html
● http://hotmath.com/hotmath_help/topics/axis-of-symmetry-of-a-parabola.
html
● http://www.virtualnerd.com/tutorials/?id=Alg1_10_2_16
● https://drive.google.com/a/harnettstudents.
org/file/d/0B5IsvLB504GyOEU4dUhSNlZ3NjA/view