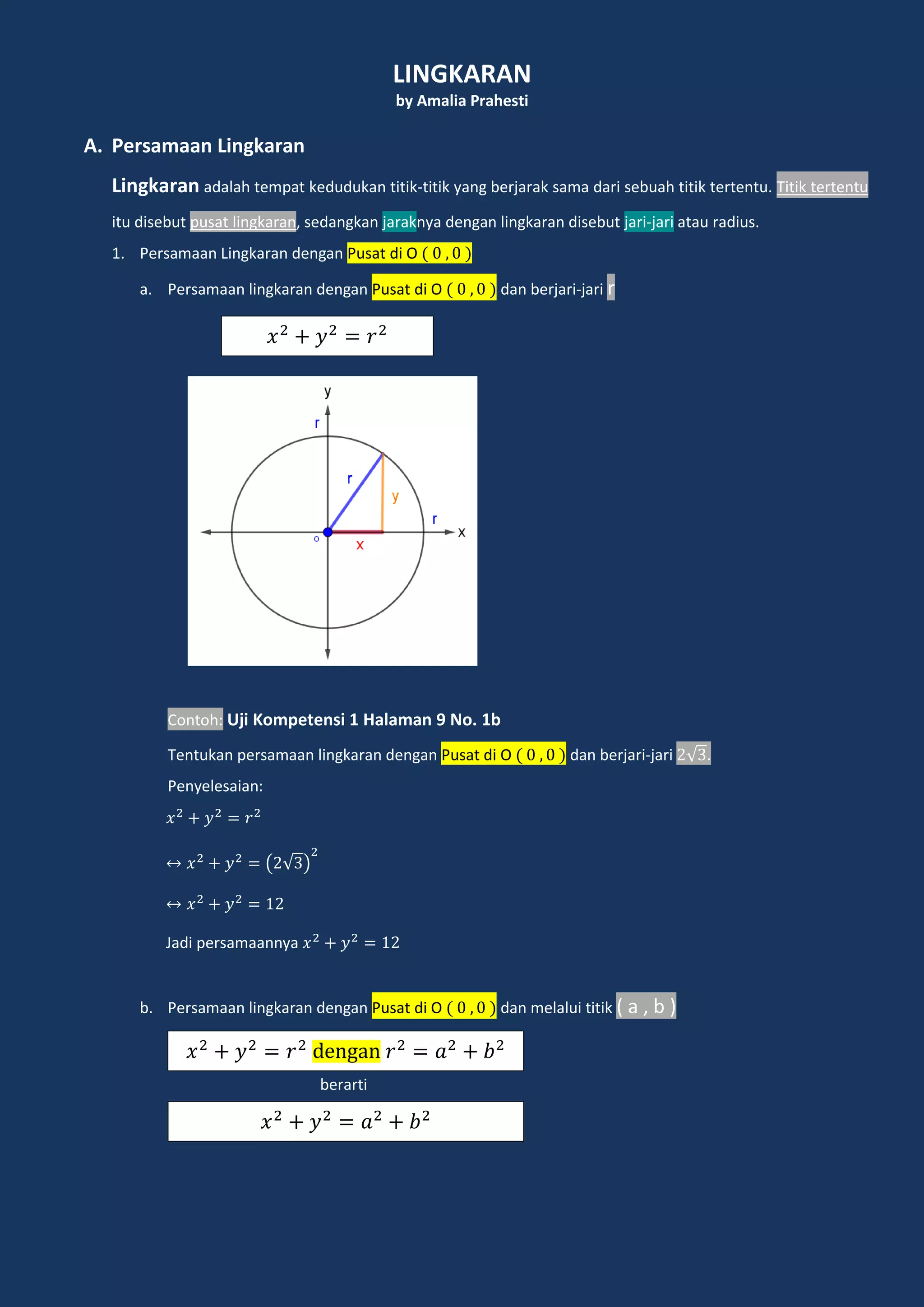
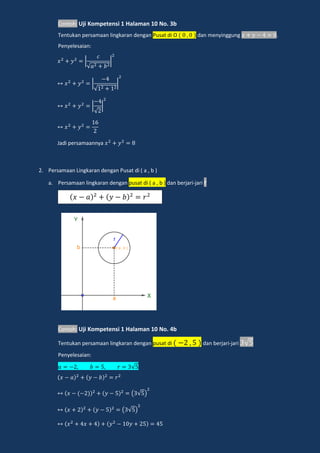
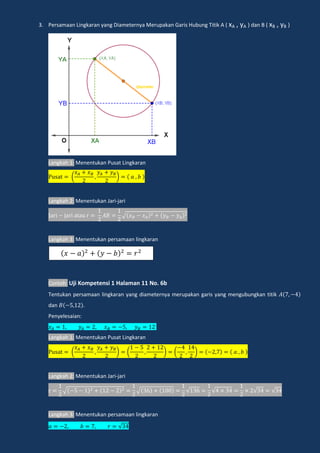
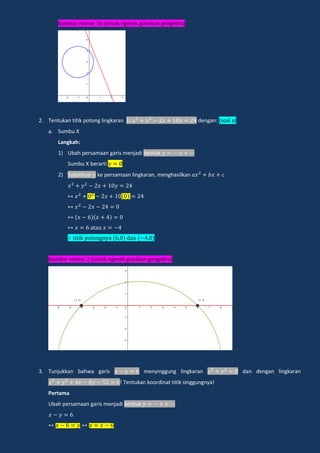
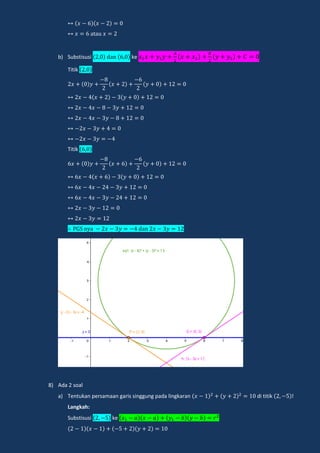
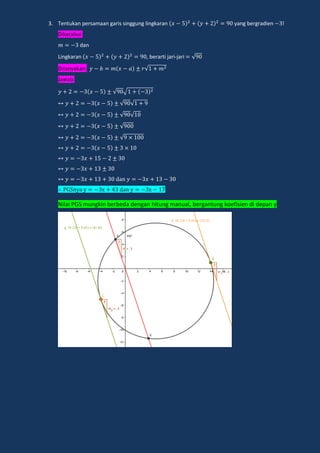
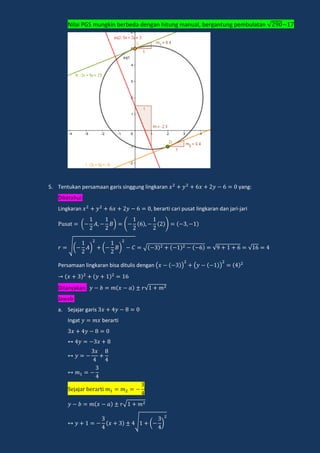
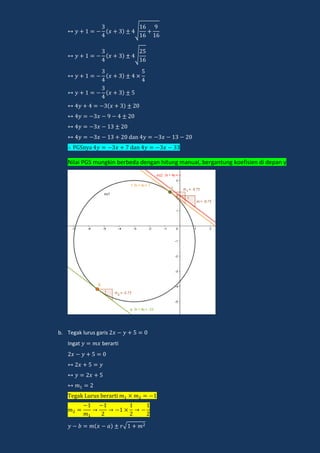
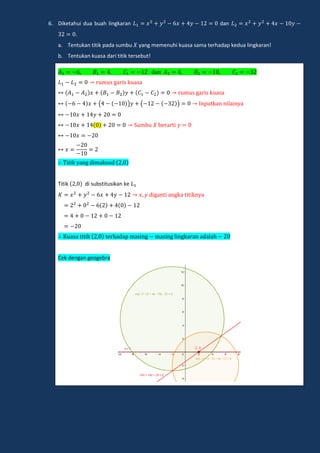
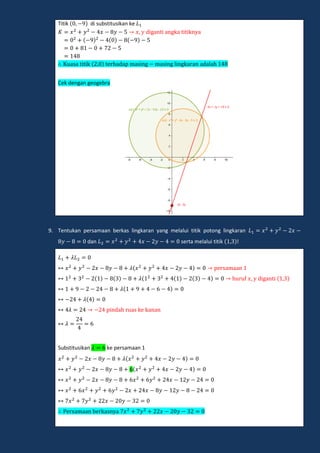
Lingkaran adalah tempat kedudukan titik-titik yang berjarak sama dari sebuah titik tertentu yang disebut pusat lingkaran. Dokumen ini menjelaskan tentang persamaan lingkaran, kedudukan titik dan garis terhadap lingkaran, serta persamaan garis singgung lingkaran.