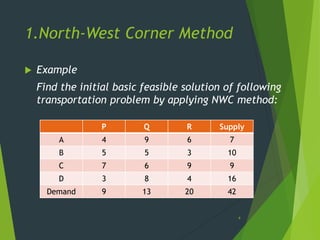
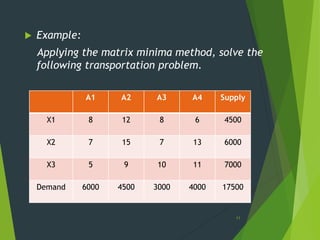
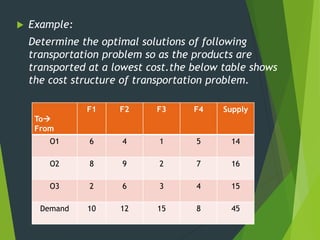
1) The document discusses three methods for finding an initial basic feasible solution to transportation problems: the North-West Corner method, Least Cost/Matrix Minimum method, and Vogel's Approximation Method. 2) The North-West Corner method works by sequentially filling cells beginning from the northwest corner based on minimum supply or demand values. 3) The Least Cost method selects the cell with the minimum unit cost and allocates the maximum possible units to it, eliminating satisfied rows and columns until complete. 4) Vogel's Approximation Method identifies row and column penalties based on cost differences and sequentially fills the cell in the row or column with the largest penalty.

1. TRANSPORTATION
PROBLEM
1
SUBMITTED TO : Mr. Kamal sanguri
Submitted By: Vivek Lohani

2. INTRODUCTION
 “The transportation problem is to transport
different amounts of a single homogeneous product ,
which are initially kept at various origins , to
different destinations with the objective of
minimising the total transportation cost”.
2

3. VARIOUS METHODS OF FINDING
INITIAL BASIC FEASIBLE SOLUTION
 The methods which are used in solving a transportation
problem to determine an initial basic feasible solution
can be summarised as follows:
3
North-West Corner(NWC) Method
Least Cost/Matrix Minimum
Method
Vogel’s Approximation
Method(VAM)

4. 1.North-West Corner Method
 Example
Find the initial basic feasible solution of following
transportation problem by applying NWC method:
4
P Q R Supply
A 4 9 6 7
B 5 5 3 10
C 7 6 9 9
D 3 8 4 16
Demand 9 13 20 42

5. Solution:
Step 1:First select the cell located at the North-west
corner of above table ,i.e. cell(A,P,).
Step 2:Now allocate the possible minimum value taken
either from supply or demand ,i.e.,
minimum(7,9)=7.Hence allocate minimum value 7 at
the cell(A,P,).
Step 3:As the whole supply (7) of A is finished hence
shift to other cell(B,P).
5

6. Step 4:Total remaining demand at the P is now 2 units. so
min(9,2)=2.allocate this unit 2 at the cell (B,P).
Step 5:Since the demand is exhausted at the cell (B,P),
we move to another cell (B,Q).here the total remaining
supply is now 8 units. so min(8,13)=8.allocate this
value 8 at the cell (B,Q).
6

7. Step 6:Total supply at the B is now finished, hence shift
to another cell (C,Q).The remaining demand at Q is 5
units. select the min(5,9)=5.allocate this unit 5 at the
cell(C,Q).
Step 7:Since the total demand at Q is now exhausted,
hence the remaining supply at the C is now 4 units.
move to another cell at (C,R).choose min(4,20)=4
units. allocate this unit 4 at the cell (C,R).
Step 8:Now remaining demand is now 16 units and total
supply is also 16 units. hence allocate this at the
cell(D,R). 7

8. P Q R Supply
A 4 9 6 7
B 5 5 3 10
C 7 6 9 9
D 3 8 4 16
Demand 9 13 20 42
8
2
7
8
5 4
16
Total transportation cost=4*7+5*2+5*8+6*5+9*4+4*16
=28+10+40+30+36+64
=208

9. 2.Least Cost/Matrix Minimum
Method
 STEPS:
Step 1:Select the cell (Oi,Dj) from the transportation
table which has the minimum unit cost and allocate
maximum possible to this cell. That row or column is
eliminated whose demand and supply requirements
are satisfied. If there is any tie in the smallest unit
cost for two or more cells then one selects that cell in
which maximum allocation is possible.
9

10. Step 2:For all remaining rows and column,adjust the
supply and demand.Repeat the process among the
remaining rows and columns with the smallest unit
cost.
Step 3:The process will continue until the supply at
various origins and demand at various destinations are
fulfilled.
10

11.  Example:
Applying the matrix minima method, solve the
following transportation problem.
11
A1 A2 A3 A4 Supply
X1 8 12 8 6 4500
X2 7 15 7 13 6000
X3 5 9 10 11 7000
Demand 6000 4500 3000 4000 17500

12. Solution:
Following allocation will appear while applying the
matrix minima method:
12
TO 
From
A1 A2 A3 A4 Supply
X1 8 12 8 6 4500/500/0
X2 7 15 7 13 6000/3000/0
X3 5 9 10 11 7000/1000/0
Demand 6000/0 4500/3500/30
00/0
3000/0 4000/0 17500
500 4000
6000
3000
1000
3000

13. Total Transportation cost=
12*500+6*4000+15*3000+7*3000+5*6000+
9*1000
=6000+24000+45000+21000+30000+9000
=135000
13

14. 3.Vogel’s Approximation
Method(VAM)
 STEPS:
 Step 1:Identify the smallest and next-to-smallest
cost in each row of the transportation table.for each
row calculate the differences between them which
are known as ‘penalties’.write the penalties of each
row and column alongside the transportation table
against the respective rows and columns.
14

15.  Step 2:Among all the rows and columns identify that
row and column which has the largest penalty.select
the cell with least cost in this identified row or column
and allocate the feasible number of units to this
cell.that row or column is eliminated whose demand
and supply requirements are satisfied.if there is any tie
in the largest penalties for two or more rows then one
selects either of them.
 Step 3:For the reduced transportation table repeat the
step 1 to calculate the column and row penalties and
then go to step 2.
Repeat the process until all the requirements are
satisfied.
15

16.  Example:
Determine the optimal solutions of following
transportation problem so as the products are
transported at a lowest cost.the below table shows
the cost structure of transportation problem.
16
To
From
F1 F2 F3 F4 Supply
O1 6 4 1 5 14
O2 8 9 2 7 16
O3 2 6 3 4 15
Demand 10 12 15 8 45

17. Solution:
To
From 
F1 F2 F3 F4 Supply
O1 6 4 1 5 14/2/0
O2 8 9 2 7 16/1/0
O3 2 6 3 4 15/5/0
Demand 10/0 12/0 15/0 8/3/1/0 45
17
10
12
15
2
1
5
4 2 1 1
3
5
1
1
1
2
1
2
2
4 2 1-
- 2 - 1
- - - 1

18. Total Transportation cost=
4*12+5*2+2*15+7*1+2*10+4*5
=48+10+30+7+20+20
=135.
18

19. 19