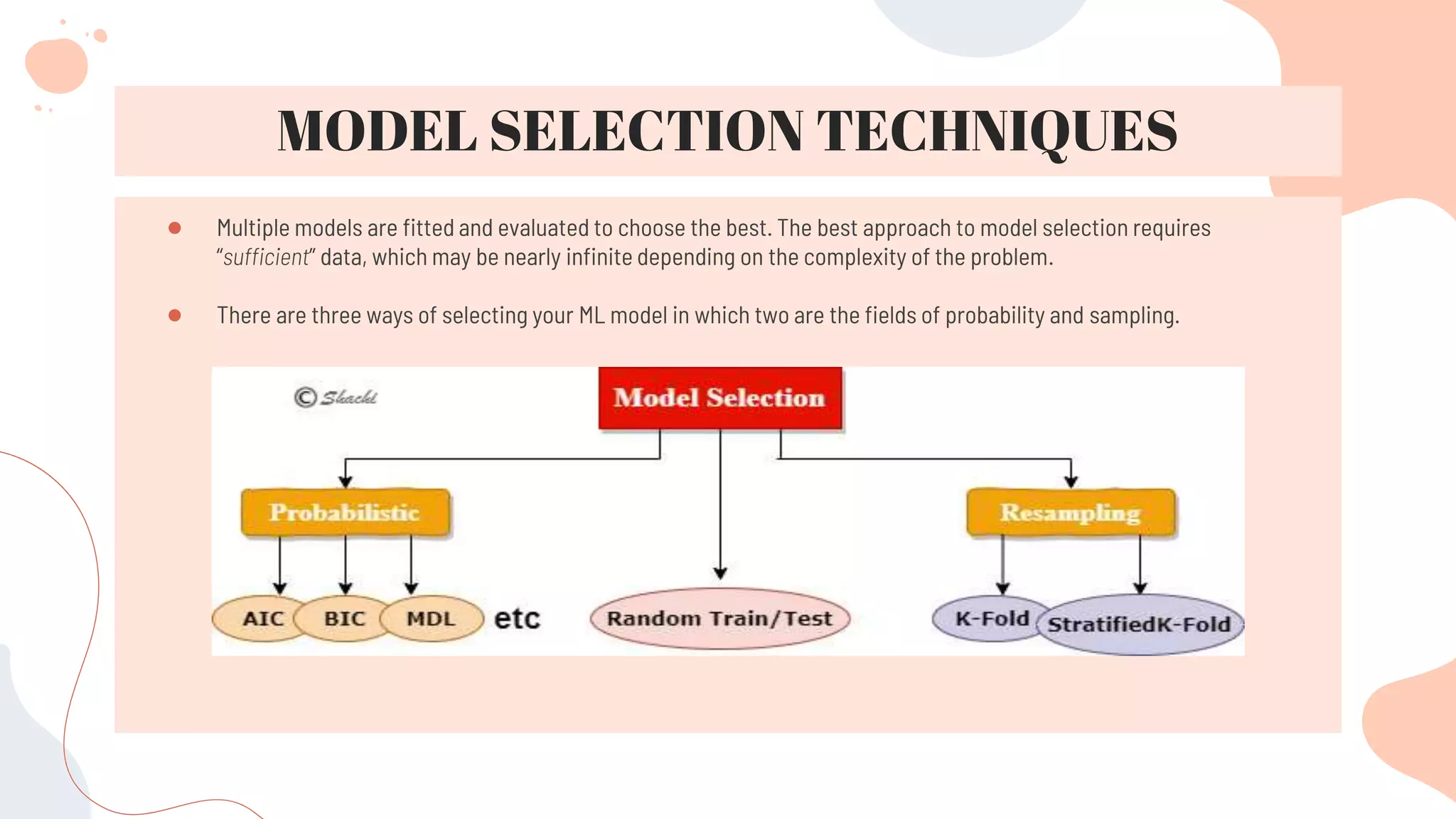
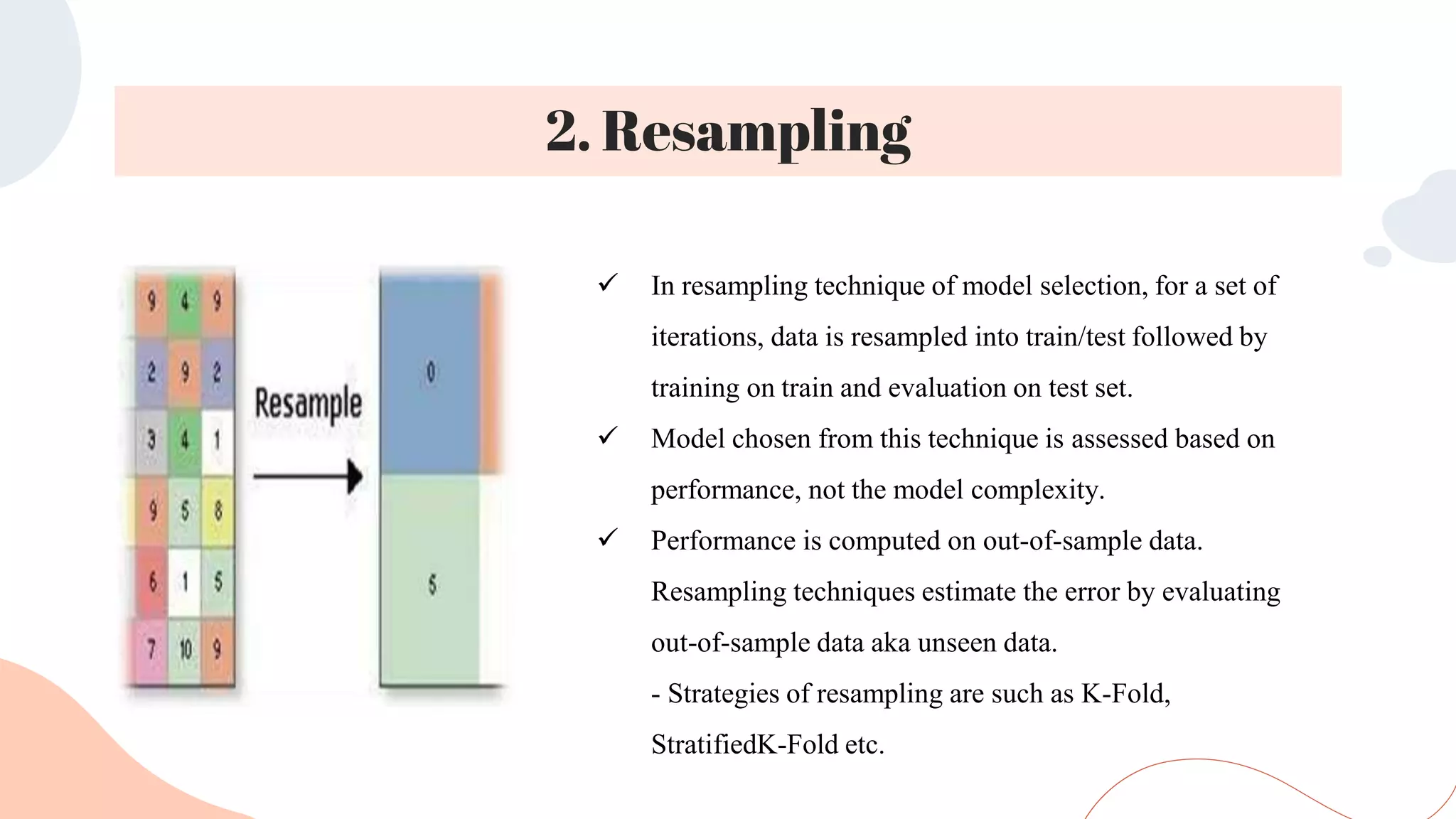
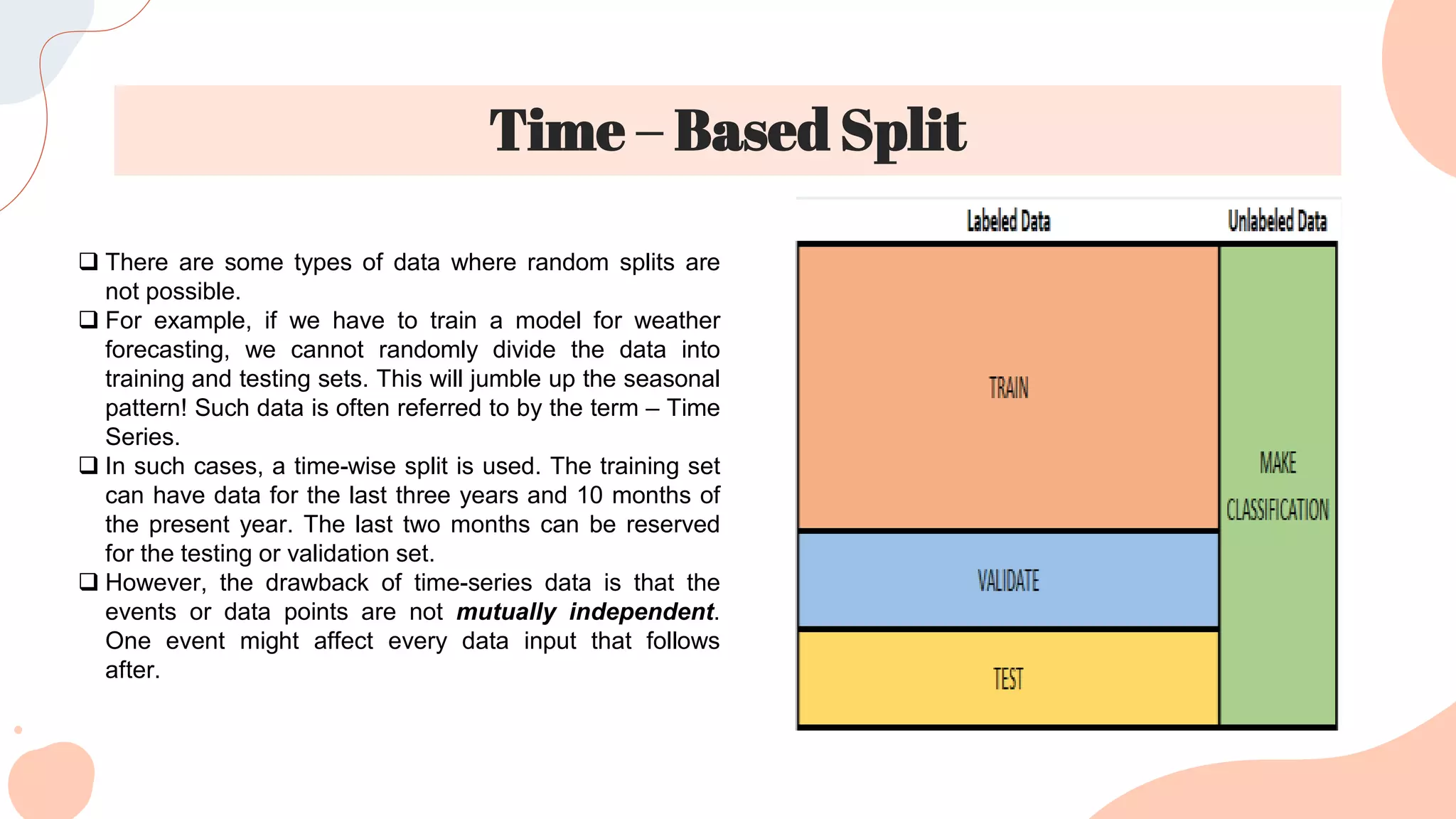
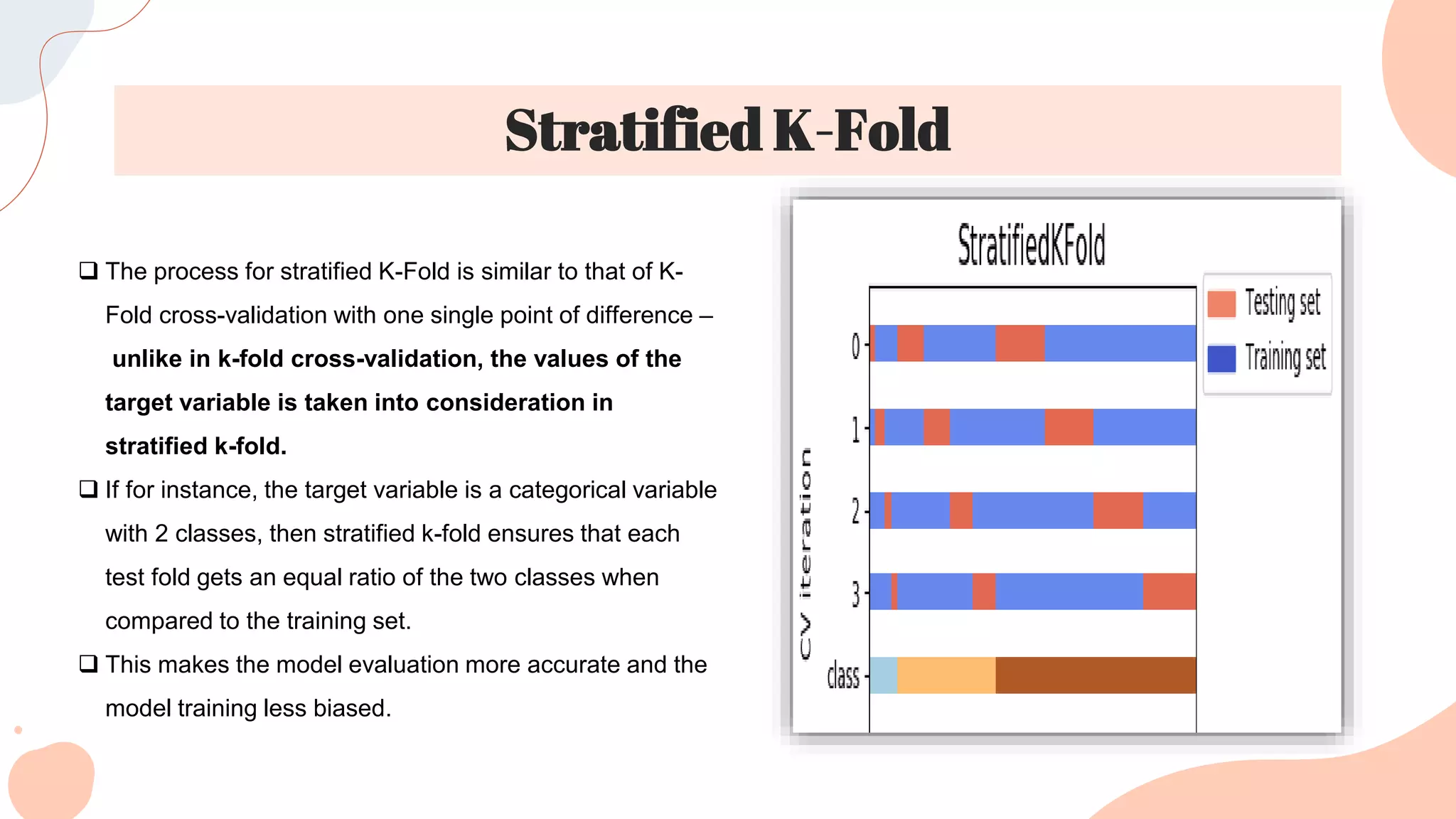
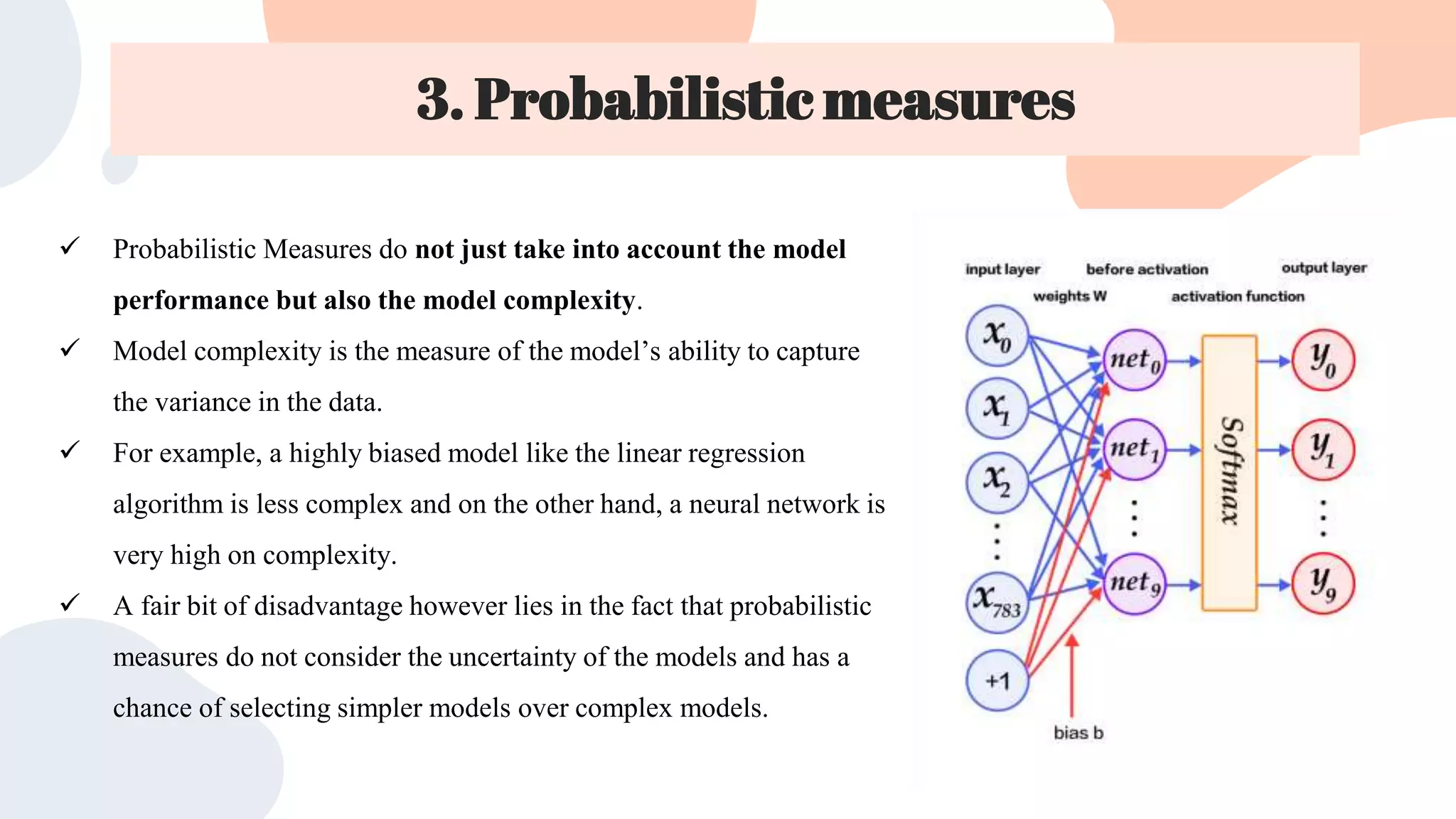
This document discusses different techniques for selecting machine learning models, including random train/test splitting, resampling methods like k-fold cross-validation and bootstrap, and probabilistic measures. Resampling techniques like k-fold cross-validation estimate error by evaluating models on out-of-sample data. Probabilistic measures consider both a model's performance and complexity, seeking to balance fit and simplicity. Common probabilistic measures mentioned are the Akaike Information Criterion, Bayesian Information Criterion, Minimum Description Length, and Structural Risk Minimization.

1. Model Selection
Techniques
- Swati (19013030)

2. Let’s start !

3. MODEL SELECTION TECHNIQUES
● Multiple models are fitted and evaluated to choose the best. The best approach to model selection requires
“sufficient” data, which may be nearly infinite depending on the complexity of the problem.
● There are three ways of selecting your ML model in which two are the fields of probability and sampling.

4. 1. Random Train/Test Split
 Random Splits are used to randomly sample a percentage of data
into training, testing, and preferably validation sets.
 Data to be passed in model is divided into train and test, ratio wise.
This can be achieved using train_test_split function of scikit-learn
python library.
 On re-running of train_test_split data code, results come out to be
different on each run of code. So, you aren’t sure how exactly your
model will perform on unseen data.
 The advantage of this method is that there is a good chance that the
original population is well represented in all the three sets. In more
formal terms, random splitting will prevent a biased sampling of data.

5. 2. Resampling
 In resampling technique of model selection, for a set of
iterations, data is resampled into train/test followed by
training on train and evaluation on test set.
 Model chosen from this technique is assessed based on
performance, not the model complexity.
 Performance is computed on out-of-sample data.
Resampling techniques estimate the error by evaluating
out-of-sample data aka unseen data.
- Strategies of resampling are such as K-Fold,
StratifiedK-Fold etc.

6. Types of Resampling
1. Time-Based Split 2. K-Fold Cross-
Validation
4. Bootstrap
3. Stratified K-Fold

7. Time – Based Split
 There are some types of data where random splits are
not possible.
 For example, if we have to train a model for weather
forecasting, we cannot randomly divide the data into
training and testing sets. This will jumble up the seasonal
pattern! Such data is often referred to by the term – Time
Series.
 In such cases, a time-wise split is used. The training set
can have data for the last three years and 10 months of
the present year. The last two months can be reserved
for the testing or validation set.
 However, the drawback of time-series data is that the
events or data points are not mutually independent.
One event might affect every data input that follows
after.

8. K-Fold Cross-Validation
 The cross-validation technique works by randomly shuffling the
dataset and then splitting it into k groups. Thereafter, on iterating
over each group, the group needs to be considered as a test set
while all other groups are clubbed together into the training set.
 The model is tested on the test group and the process continues for
k groups.
 Thus, by the end of the process, one has k different results on k
different test groups. The best model can then be selected easily by
choosing the one with the highest score.

9. Stratified K-Fold
 The process for stratified K-Fold is similar to that of K-
Fold cross-validation with one single point of difference –
unlike in k-fold cross-validation, the values of the
target variable is taken into consideration in
stratified k-fold.
 If for instance, the target variable is a categorical variable
with 2 classes, then stratified k-fold ensures that each
test fold gets an equal ratio of the two classes when
compared to the training set.
 This makes the model evaluation more accurate and the
model training less biased.

10. Bootstrap
 Bootstrap is one of the most powerful ways to obtain a stabilized model.
 The first step is to select a sample size (which is usually equal to the size of
the original dataset). Thereafter, a sample data point must be randomly
selected from the original dataset and added to the bootstrap sample. After
the addition, the sample needs to be put back into the original sample. This
process needs to be repeated for N times, where N is the sample size.
 Therefore, it is a resampling technique that creates the bootstrap sample
by sampling data points from the original dataset with replacement.
 The model is trained on the bootstrap sample and then evaluated on all
those data points that did not make it to the bootstrapped sample. These
are called the out-of-bag samples.

11. 3. Probabilistic measures
 Probabilistic Measures do not just take into account the model
performance but also the model complexity.
 Model complexity is the measure of the model’s ability to capture
the variance in the data.
 For example, a highly biased model like the linear regression
algorithm is less complex and on the other hand, a neural network is
very high on complexity.
 A fair bit of disadvantage however lies in the fact that probabilistic
measures do not consider the uncertainty of the models and has a
chance of selecting simpler models over complex models.
e

12. o SRM tries to balance out the
model’s complexity against its
success at fitting on the data.
o MDL or the minimum description
length is the minimum number of
such bits required to represent the
model.
o BIC penalizes the model for its
complexity and is preferably used
when the size of the dataset is not
very small .
o AIC is the measure of information
loss.
2. Bayesian Information Criterion (BIC)
1. Akaike Information Criterion (AIC)
4. Structural Risk Minimization (SRM)
3. Minimum Description Length (MDL)
Types of Probabilistic measures

13. Thank You !!
For more Information visit on :
(https://neptune.ai/blog/the-ultimate-guide-to-evaluation-and-selection-of-
models-in-machine-learning)