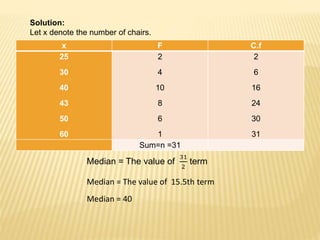
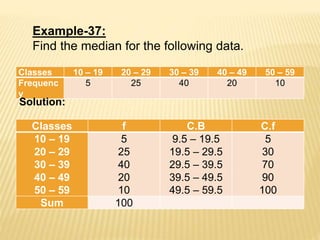
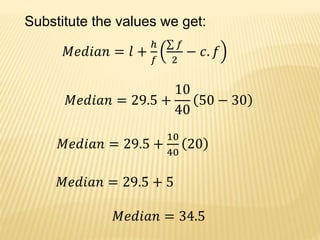The median of a dataset is the middle value when the observations are arranged in ascending order. It is the value below which 50% of the observations lie. For an odd number of observations, the median is the middle value. For an even number, the median is the average of the two middle values. The median can be calculated for both grouped and ungrouped data using different formulas depending on whether the data is grouped by value or range. Examples are provided to demonstrate calculating the median for different types of datasets.

1. MEDIAN
NADEEM UDDIN
ASSOCIATE PROFESSOR
OF STATISTICS

2. MEDIAN:
The median of a set of
observations is the value that
falls in the middle when the
observation are arranged in order
of magnitude
or the median is a value at or
below which 50% of the ordered
data lie.

3. Calculating the Median:
In case of ungroup data, the median can be
found by the following formula.
𝑀𝑒𝑑𝑖𝑎𝑛 =
𝑛 + 1
2
𝑡ℎ 𝑣𝑎𝑙𝑢𝑒, 𝑖𝑓 𝑛 𝑖𝑠 𝑜𝑑𝑑
𝑀𝑒𝑑𝑖𝑎𝑛 =
𝑛
2
𝑡ℎ 𝑣𝑎𝑙𝑢𝑒 +
𝑛 + 2
2
𝑡ℎ 𝑣𝑎𝑙𝑢𝑒
2
, 𝑖𝑓 𝑛 𝑖𝑠 𝑒𝑣𝑒𝑛
n = Number of Terms or Observation

4. Example-33:
The wages of 7 workers in rupees are 3000,
4500, 5000, 2500, 4000, 2000, 3200.
Solution:
1st, we arranging the observation in ascending
order. We get 2000, 2500, 3000, 3200, 4000,
4500, 5000
Median = The value of th
2
1n





 
term
Median = The value of th
2
17





 
term
= The value of 4th
term
Median = Rs. 3200

5. Example-34:
The minimum temperature in Quetta for the first 10
days of February was 10, 10, 0, 4, 3, 8, 4, 3, 5, 1
Solution:
1st, we arranging the observation in ascending order.
We get 10, 8, 4, 3, 0, 1, 3, 4, 5, 10.
𝑀𝑒𝑑𝑖𝑎𝑛 =
𝑛
2
𝑡ℎ 𝑣𝑎𝑙𝑢𝑒 +
𝑛 + 2
2
𝑡ℎ 𝑣𝑎𝑙𝑢𝑒
2
𝑀𝑒𝑑𝑖𝑎𝑛 =
10
2
𝑡ℎ 𝑣𝑎𝑙𝑢𝑒+
10+2
2
𝑡ℎ 𝑣𝑎𝑙𝑢𝑒
2
𝑀𝑒𝑑𝑖𝑎𝑛 =
5𝑡ℎ 𝑣𝑎𝑙𝑢𝑒+6𝑡ℎ 𝑣𝑎𝑙𝑢𝑒
2
𝑀𝑒𝑑𝑖𝑎𝑛 =
0+1
2
= 0.5

6. In case of group data with classes
consisting of single values, the
median can be found by the
following formula.
Median = The value of
𝑛
2
term
Where,
n = Sum of the frequencies

7. No. of
Chairs
25 30 40 43 50 60
No. of
Rooms
2 4 10 8 6 1
Example-35:
Given below is the frequency distribution of
number of chairs in different rooms of a
college. Find the median.

8. Solution:
Let x denote the number of chairs.
Median = The value of
31
2
term
Median = The value of 15.5th term
Median = 40
x F C.f
25
30
40
43
50
60
2
4
10
8
6
1
2
6
16
24
30
31
Sum=n =31

9. In case of group data with classes consisting of
range, the median can be found by the following
formula
𝑀𝑒𝑑𝑖𝑎𝑛 = 𝑙 +
ℎ
𝑓
𝑓
2
− 𝑐. 𝑓
Where,
l = Lower class boundary of the median
class
Median Class: The class corresponding to
the cumulative frequency in which
𝑓
2
lies.
h = Size of class interval of the median
class
f = Frequency of the median class
𝑓 = Sum of the frequencies
C.f = Cumulative frequency of the class

10. Example-37:
Find the median for the following data.
Classes 10 – 19 20 – 29 30 – 39 40 – 49 50 – 59
Frequenc
y
5 25 40 20 10
Solution:
Classes f C.B C.f
10 – 19
20 – 29
30 – 39
40 – 49
50 – 59
5
25
40
20
10
9.5 – 19.5
19.5 – 29.5
29.5 – 39.5
39.5 – 49.5
49.5 – 59.5
5
30
70
90
100
Sum 100

11. 1st, find the median class:
𝑓
2
𝑡ℎ term =
100
2
term = 50th term
50th term lies in the class 30 – 39.
Therefore, 29.5 – 39.5 is the
medianclass.
l = 29.5,
h = 39.5 – 29.5 = 10,
f = 40,
𝑓
2
= 50,
C.f =30

12. Substitute the values we get:
𝑀𝑒𝑑𝑖𝑎𝑛 = 𝑙 +
ℎ
𝑓
𝑓
2
− 𝑐. 𝑓
𝑀𝑒𝑑𝑖𝑎𝑛 = 29.5 +
10
40
50 − 30
𝑀𝑒𝑑𝑖𝑎𝑛 = 29.5 +
10
40
20
𝑀𝑒𝑑𝑖𝑎𝑛 = 29.5 + 5
𝑀𝑒𝑑𝑖𝑎𝑛 = 34.5