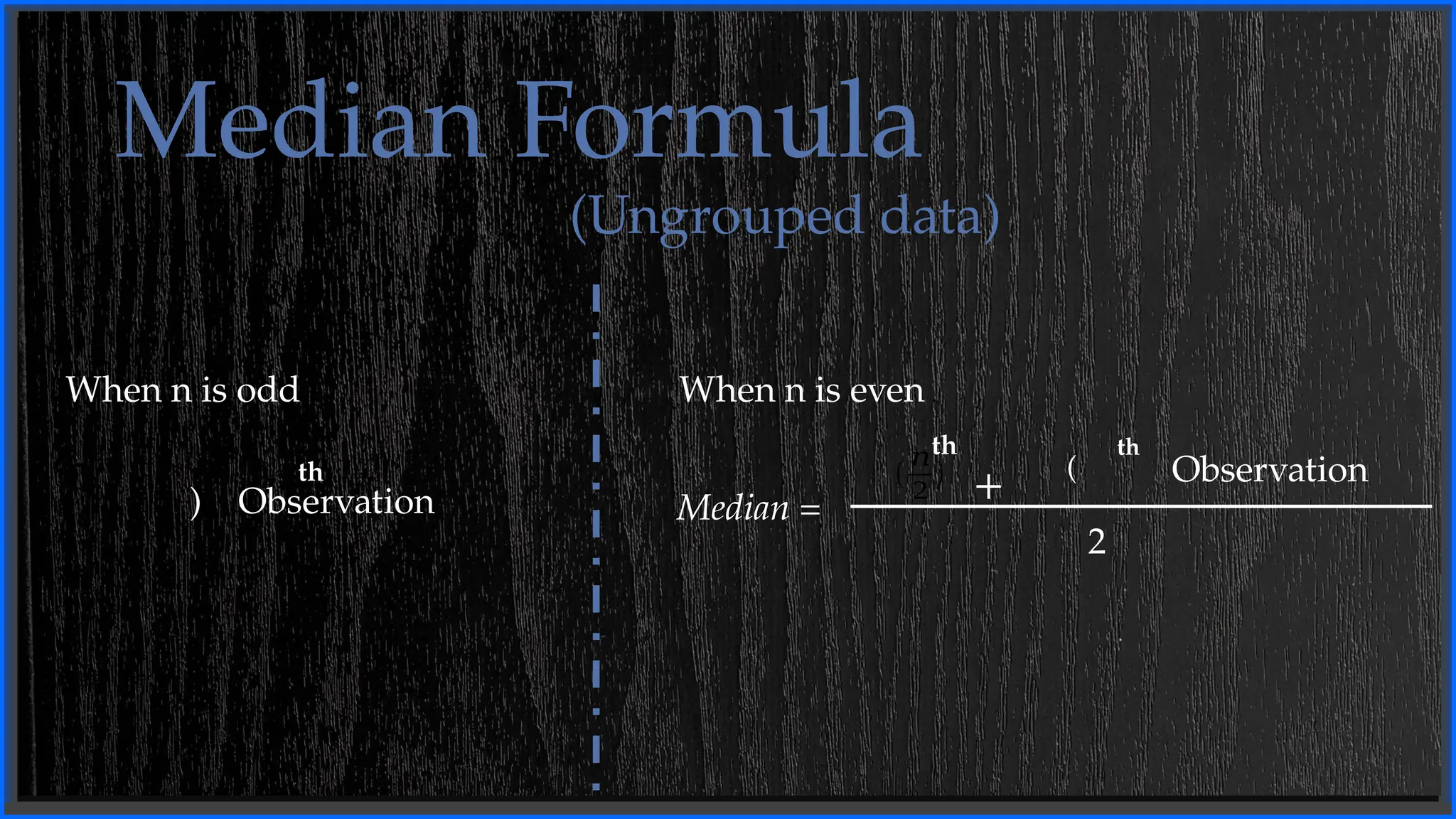
This presentation explores the concept of the median in mathematics, a fundamental measure of central tendency. The median represents the middle value in a sorted dataset, making it a crucial tool in statistics and data analysis. Unlike the mean, the median is resistant to extreme values, making it particularly useful for skewed distributions. Topics covered include how to calculate the median for odd and even datasets, its significance in real-world applications, and comparisons with other statistical measures like the mean and mode. This guide is ideal for students, educators, and anyone interested in mastering basic statistical concepts.

1. Median

2. Median
The median of a set of data is the middlemost number or center value in the set.
The median is also the number that is halfway into the set.
Condition:
Sorted data
Example:
The set of numbers is
2, 3,4 ,6, 8, 9, 11
Median

3. Median Formula
(Ungrouped data)
th
When n is even
2
Median =
th
Observation
th
+
) Observation
When n is odd
(
𝑛
2
) (

4. Example (Odd Number)
102, 56, 34, 99, 89, 101, 10.
 Step 1:
Sort your data from the smallest number to the highest number.
10, 34, 56, 89, 99, 101, 102.
 Step 2:
Find the value of n
n = 7
 Step 3:
Find ()th number
() or 4th
number = 89 (Median)

5. Example (Even Number)
102, 56, 34, 99, 89, 101, 10, 54
 Step 1:
Place the data in ascending order.
10, 34, 54, 56, 89, 99, 101, 102.
 Step 2:
Find the value of n
n = 8

6. Step 3:
Find ( )th and (+1)th numbers.
10, 34, 54, 56, 89, 99, 101, 102
Step 4:
Add the two middle numbers and then divide by two, to get
the average:
56 + 89 = 145
145 / 2 = 72.5.
The median is 72.5.

7. Median Formula
(Grouped data)
𝑀𝑒𝑑𝑖𝑎𝑛=𝑙+
𝑛
2
−𝑐𝑓
𝑓
×𝑖
Here,
l = lower boundary point of median class
n = Total frequency
cf = Cumulative frequency of the class preceding the median class
f = Frequency of the median class
i = class width of the median class

8. Example
Class 0-10 10-20 20-30 30-40 40-50 50-60 60-70
Frequency 15 20 25 24 22 14 5
Find the Median of the following distribution

9. Class Frequency
(f)
Cumulative
Frequency
(cf)
0 - 10 15 15
10 – 20 20 35
20 – 30 25 60
30 – 40 24 84
40 – 50 22 106
50 – 60 14 120
60 - 70 5 125
Total n = 125

10. Here,
n = 125
So, median = Measure of
63rd term is situated in the class (30 - 40)
Thus median class is (30 - 40)
= 31.04
Here,
l = 30
n = 125
cf = 60
f = 24
i = 10
𝑀𝑒𝑑𝑖𝑎𝑛=𝑙+
𝑛
2
−𝑐𝑓
𝑓
×𝑖

11. Thankyou