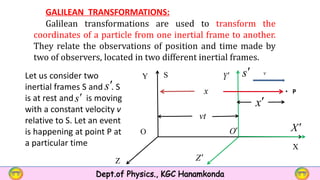
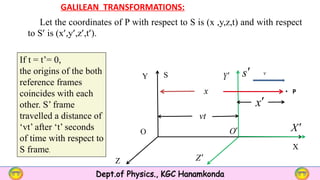
This document provides an introduction to the special theory of relativity, including: - It defines the special theory of relativity as dealing with objects moving at constant speeds, while the general theory deals with accelerating objects. - Frames of reference and inertial frames are introduced, with inertial frames obeying Newton's laws of motion. - Galilean transformations are described as relating the coordinates of particles between inertial frames, including equations for position, velocity, acceleration, and forces. - The drawbacks of Galilean transformations are that they are invalid for objects moving at the speed of light or for electromagnetism.

1. Special Theory of Relativity-Lecture– 1
B.Sc. Physics - First Year - First Semester
Topic: Introduction- Galilean Transformations

2. Special Theory of Relativity
The position, and the time are relative physical
quantities
As these physical quantities are relative, motion is also
relative.
The theory which deals with the relativity of motion
and rest is called the Theory of relativity.
It is divided into two parts.
1. Special Theory of Relativity,
2. General theory of relativity

3. .
The Special theory of relativity deals with objects or systems which
are moving at a constant speed with respect to another or at rest.
The general theory of relativity deals with objects or systems which
are speeding up or slowing down with respect to one another.
Frame of Reference:
A well defined coordinate system which specifies the
position and motion of the objects or systems is called
Frame of Reference

4. A system relative to which the motion of any object is described is
called a frame of reference. Or
A well defined coordinate system, which can explain the motion of
the objects, is called Frame of Reference.
X
Y
Z
O
P ( x ,y , z )
.
The motion of a body has no meaning
unless it is described with respect to
some well defined system. There are
generally two types of reference systems:
1.Inertial frames
or un accelerated frames,
2. Non-inertial frames.

5.  A frame of reference is said to be inertial when the objects in this
frame obey Newton’s law of inertia and other laws of Newtonian
mechanics.
In inertial frame, every object not acted upon by an external force,
is at rest or moves with constant velocity.
 A frame of reference moving with constant velocity relative to an
inertial frame is also inertial. Since, acceleration of the object in both
the frames is zero, the velocity of the object is different but uniform.
Inertial Frames:

6. Non-inertial frame:
A frame of reference is said to be non-inertial when the
objects in this frame do not obey Newton’s law of inertia or
Newton’s laws of motion.
In non-inertial frame, every object acted upon by an
external force, is accelerated.

7. GALILEAN TRANSFORMATIONS:
Galilean transformations are used to transform the
coordinates of a particle from one inertial frame to another.
They relate the observations of position and time made by
two of observers, located in two different inertial frames.
Let us consider two
inertial frames S and . S
is at rest and is moving
with a constant velocity v
relative to S. Let an event
is happening at point P at
a particular time
s
s
s
S
Y
Z
X
O O X
Y v
. P
x
x
vt
Z

8. GALILEAN TRANSFORMATIONS:
s
S
Y
Z
X
O O X
Y v
. P
x
x
vt
Z
Let the coordinates of P with respect to S is (x ,y,z,t) and with respect
to S’ is (x’,y’,z’,t’).
If t = t’= 0,
the origins of the both
reference frames
coincides with each
other. S’ frame
travelled a distance of
‘vt’ after ‘t’ seconds
of time with respect to
S frame.

9. Let us choose our axes so that X and X’ are parallel to v. Then the
relation between these two frames can be written as
,
t
t
z
z
y
y
vt
x
x









( there is no relative motion along Y and Z
axes )
( time is independent of space coordinate system )
The above equations are known as Galilean transformations.

10. The inverse Galilean transformations can be expressed as under
,
t
t
z
z
y
y
vt
x
x









Galilean transformation for velocity can be written as:
z
z
y
y
x
x
x
u
u
u
u
v
u
u
v
dt
dx
dt
vt
x
d
dt
x
d
u
















,
v
-
u
u
form
in vector
)
(

11. Galilean transformation for acceleration
The acceleration components can be obtained by differentiating
velocity equations with respect to time.
a
a
a
a
a
a
a
a
dt
dv
dt
du
dt
v
u
d
dt
u
d
a
z
z
y
y
x
x
x
x
x
x
















,
constant)
is
v
velocity
(
)
(

In vector form, aˈ = a Multiplying above equation with mass on both
sides, we get
maˈ = ma

12. F ˈ= F
The acceleration is same in both S and S’
frames. So, acceleration and force are invariant in
classical physics.
Drawbacks of Galilean Transformations:
1.The laws of electromagnetism or electrodynamics
and Maxwell’s equations are not invariant under
Galilean transformations.
2.Galilean transformations are invalid when the
objects are moving with nearer velocities of velocity
of light.

13. ASSIGNMENT
1.What is theory of relativity and explain
2.Define frame of reference
3.Distinguish between inertial and non inertial frames
4.Derive Galilean Transformation equations, and write its drawbacks