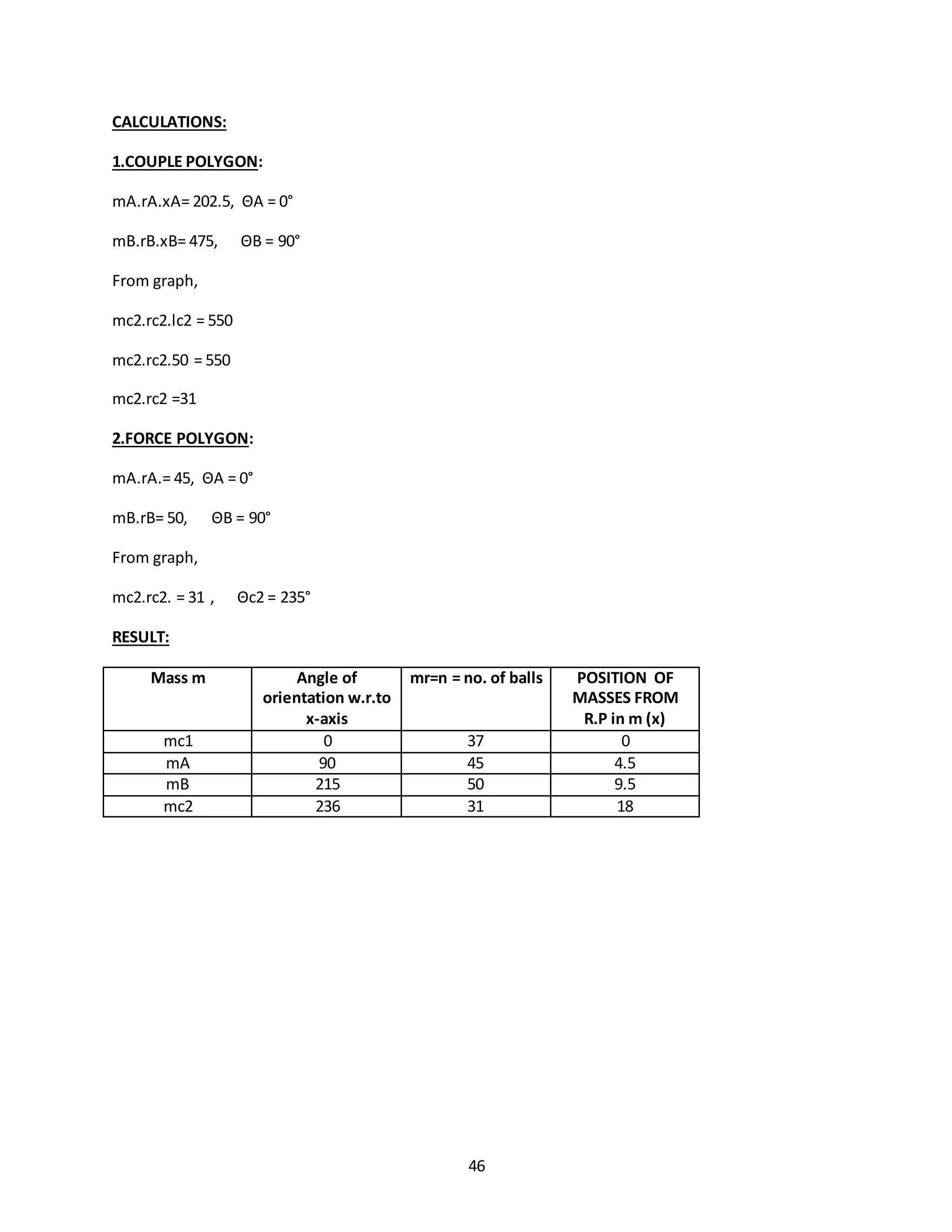
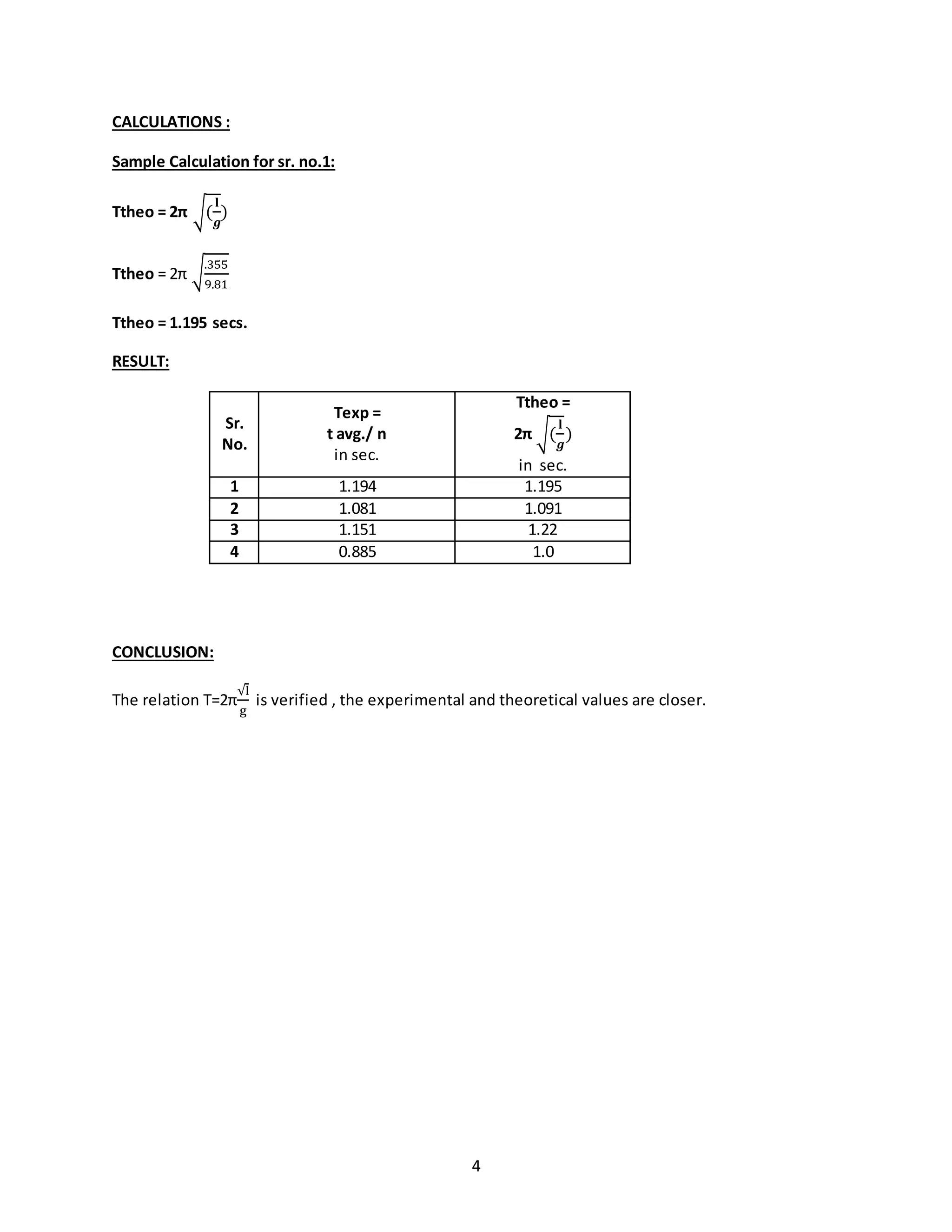
1. The document describes 5 experiments related to mechanical oscillations and vibrations. Experiment 1 verifies the relation between the period of a simple pendulum and its length. Experiment 2 determines the radius of gyration of a compound pendulum. 2. Experiment 3 uses a bifilar suspension to determine the radius of gyration of a bar. Experiment 4 studies longitudinal vibrations of a helical spring and determines the frequency theoretically and experimentally. 3. Experiment 5 examines vibrations of a system with springs in series. Each experiment involves setting up the apparatus, collecting observations in tables, performing calculations, and drawing conclusions by comparing experimental and theoretical results.

1. 1
EXPERIMENT NO.1

2. 2
Experiment No 1.
SIMPLE PENDULUM
AIM: To verify the relation.
T = 2π √(
𝐥
𝒈
)
Where T= Periodic Time in Seconds.
l= Length of Pendulum in cms.
DESCRIPTION OF SET UP :
For conducting the experiment, a bar is supported by nylon thread into the hook. It is
possible tochange the lengthof the pendulum.Thismakesitpossible to study the effect of variation of
length on periodic time.A small ball may be substituted for large ball to illustrate that the period of
oscillation is independent of the mass of ball.
THEORY :
Simple pendulum
By equilibrium of forces we have;
mg = Tcos dθ ≈ T ……..(1)
By S.H.Mequation we have;
T sin dθ = mω2
x ……..(2)
we have; x = l sin dθ
Hence eqn.(2) becomes

3. 3
T sin dθ = mω2
l sin dθ
T = mω2
l ……..(3)
From (1) and (3)
mg = mω2
l
ω2
= (g / l) ;ω = √(g/l)
we have ; ω = 2 π / T
Hence,T = 2π √(
l
𝑔
)
PROCEDURE:
a] Attach each ball to one end of the thread.
b] Allowthe ball tooscillate anddeterminethe periodictime Tbyknowingtime (forsay 10 oscillations).
c] Repeat the experiment by changing the length.
d] Complete the observation table given below.
OBSERVATIONS:
Weight of small ball: 112 gms.
Weight of largel ball: 60 gms.
OBSERVATION TABLE :
Sr.No.
Mass of the ball
(m) in gms.
Length
(L) In cms.
No.of osc.
(n)
Time for n
oscillation (t) in
sec.
Texp =
t avg./ n in
sec.
Ttheo =
2π √(
𝐥
𝒈
)
in sec.
1 112 35.5 10
11.82
11.95
12.06
1.194 1.195
2 112 29.5 10
10.75
10.79
10.90
1.081 1.091
3 60 37 10
11.44
11.59
11.49
1.151 1.22
4 60 25 10
8.41
8.66
8.50
0.885 1

4. 4
CALCULATIONS :
Sample Calculation for sr. no.1:
Ttheo = 2π √(
𝐥
𝒈
)
Ttheo = 2π √
.355
9.81
Ttheo = 1.195 secs.
RESULT:
Sr.
No.
Texp =
t avg./ n
in sec.
Ttheo =
2π √(
𝐥
𝒈
)
in sec.
1 1.194 1.195
2 1.081 1.091
3 1.151 1.22
4 0.885 1.0
CONCLUSION:
The relation T=2π
√l
g
is verified , the experimental and theoretical values are closer.

5. 5
EXPERIMENT NO.02

6. 6
Experiment No 2.
COMPOUND PENDULUM
AIM: To Determine radius of gyration K of givencompound pendulumto verifythe relation.
T=2π √((𝒌 𝟐+𝑶𝑮 𝟐) / (g*OG))
Where T= Periodictime insec.
K=Radiusof gyration aboutC.G incm.
OG= Distance of CG of rod from support.
L= Lengthof suspended pendulumincm.
DISCRIPTION OF SET UP:
The compoundpendulumconsistsof steelbar.The bar issupportedinthe hole byknife edge.
THEORY:
Compoundpendulum
The systemwhichissuspendedverticallyandoscillateswithasmall amplitudeunderthe actionof
forvce of gravity, is knownas“compoundpendulum”.Itisan example of undampedsingle degree of
freedomsystem.
Let,W = Weightof rigidbody.
W = mg , m = W/g
O = Pointof suspension.
k = radiusof gyrationaboutan axisthroughthe centre of gravityG.
h = distance of pointof suspensionfromG.
I = Momentof inertiaof bodyaboutO.

7. 7
= m𝑘2 + 𝑚ℎ2
If OG isdisplacedbyanangle ‘θ’, restoringtorque T.
T = -h W sinθ
= -mghsinθ
If θ isverysmall,thensinθ= θ , thenabve equationcanbe writtenas,
T = -mghθ
Inertiatorque isgivenas,
T = -I θ
Summingupall momentsactingonthe body,
Iθ + mgh = 0
The natural frequencyωn canbe determinedas
ωn = √(
𝑚𝑔ℎ
𝐼
)
also,
ωn = √(
𝑚𝑔ℎ
𝑚𝑘²+𝑚ℎ²
)
ωn = √
𝑔ℎ
𝑘²+ℎ²
fn =
1
2𝛑
√
𝑔ℎ
𝑘²+ℎ²
PROCEUDRE:
1] Supportthe rod knife edge.
2] Note the lengthof suspendedpendulumanddetermine OG.
3] Allow the barto oscillate and determine‘ T ’ byknowingtime for10 oscillations.
4] Repeatthe above procedure withthe secondpendulum.
5] Complete the observationtable givenbelow.

8. 8
OBSERVATIONS:
1. OG = 32cm. forsmall pendulum.
2. OG = 42cm. forlarge pendulum.
3. msmall = 616 gms.
4. mlarge = 1.5 kg.
5. ktheo. = L/2√3
OBSERVATION TABLE :
CALCULATION :
Sample Calculation for sr. no.1:
1.Finding Kexpt. We have: T=2π √((𝑘2+𝑂𝐺2) / (g*OG))
1.246=2π √((𝑘2+0.322) / (9.81*0.32)) ; Kexpt.= 0.145 cm
2.Finding Ktheo.
We have: ktheo. = L/2√3
ktheo. = 32/2 ; ktheo. = 9.23 cm
RESULT:
Sr.
No.
kexp =
in m.
ktheo =
= L/2√3 in m.
1 0.145 0.168
2 0.2 0.2309
CONCLUSION:
Radiusof gyrationis calculatedandfoundtomatch withthe relation T=2π √((𝒌 𝟐+𝑶𝑮 𝟐) / (g*OG)),
hence experimentisverified.
Sr.
No.
L
in cm
OG
In cm
No. of
osc.( n)
Time for n
osc (t) in
sec
Texp =
tavg./n
in sec.
kexpt
.in m
Ktheo
. In m
1 58.5 32 10
12.16
12.88
12.34
1.246 0.145 0.168
2 80 42 10
14.63
14.31
14.25
1.439 0.2 0.2309

9. 9
EXPERIMENT NO.3

10. 10
Experiment No 3.
BIFILAR SUSPENSION
AIM:
To determine the radiusof gyrationof givenbarbyusingbifilarsuspension.
DESCRIPTION: OF SET UP:
A uniform rectangular section bar is suspended form the pendulum support frame by two
parallel cords. Top ends of cords are attached to hooks filed at the top. The other ends are secured in the
bifilar bar.It is possible to change the length of cord or decrease its width.
The suspension may also use to determine the radius of gyration of anybody under
investigation the body bolted to the centre. Radius of gyration of the combined bar and body is then
determined.
THEORY:
Bifilar suspension
In bifilar suspension a weight W is suspended by two long flexible strings.
Initially the support and the bar AB are parallel.The bar AB is given a slight twist Ɵ and then released.
Let the strings are displaced by an angles Φ1 and Φ2.If l1 and l2 are distance of two ends from the centre of
gravity G, then tension TA and TB can be written as,
TA = (Wl2)/(l1 + l2) and TB = (Wl1)/(l1 + l2) …………(1)
Since the Φ1and Φ2 angles are small, so the effects of vertical acceleration can be neglected.Only the
horizontal components of tension will be considered which are given as
TA Φ1 and TB Φ2 and both are perpendicular to AB. TA = (Wl2)/(l1 + l2) and TB = (Wl1)/(l1 + l2)

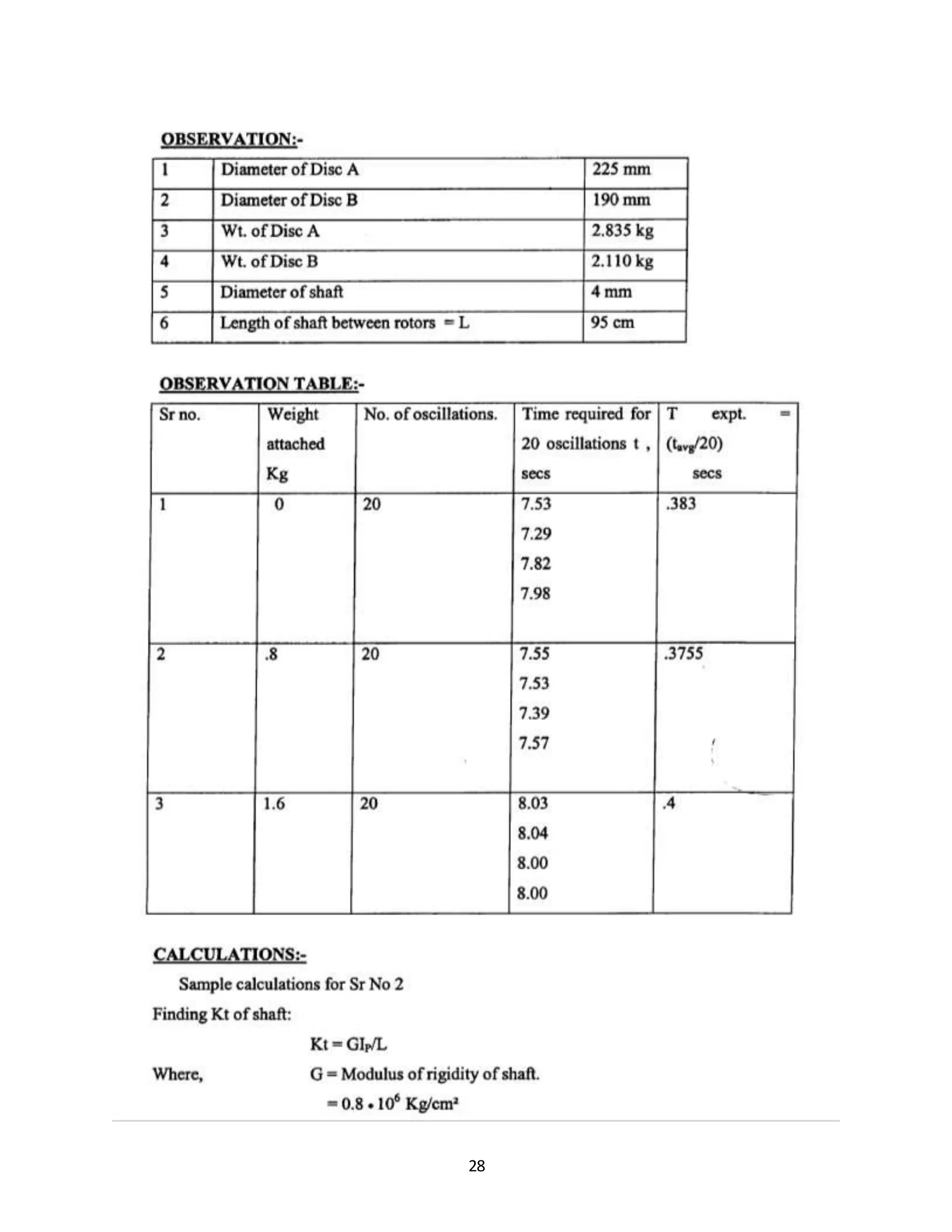
11. 11
From the geometry
l1Ɵ = l Φ1 and l2Ɵ = l Φ2
or Φ1 = l1Ɵ / l , Φ2 = l2Ɵ / l ………………(2)
The resisting torque T for the system can be written as
T = TA l1 Φ1 +TB l2 Φ2
=[(Wl2)/(l1 + l2) ]*[(( l1Ɵ) / l)]*l1 + [(Wl1)/(l1 + l2)]*[(( l2Ɵ) / l)]*l2
Substituting TA and TB from (1) and Φ1and Φ2 from (2)
= [(W l2 l1 Ɵ) /(l1 + l2)l]*[( l1 + l2)]
= (W l2 l1 Ɵ)/ l ………..(3)
We know that
T = I α
Where , T = torque
I = Moment of inertia = W k2
/ g
α = angular acceleration
k = radius of gyration
So, α = T/I
= ( (W l2 l1 Ɵ)/ l)/ (W k2
/ g)
= (g l2 l1 Ɵ) / l k2
……….(4)
We also know that
ω2
= Angular acceleration / Angular Displacement
Where, ω = Angular velocity of AB
ω2
= (g l2 l1 Ɵ) / l k2
θ
ω2
= (g l2 l1 ) / l k2

12. 12
Here, l2 = l1= a
ω2
= (g a2
) / l k2
ω = (a/k)√(𝑔/𝑙)
We have ω = 2π/T
Hence T = 2π *(k/a)√(𝒍/𝒈) ………(5)
PROCEDURE:
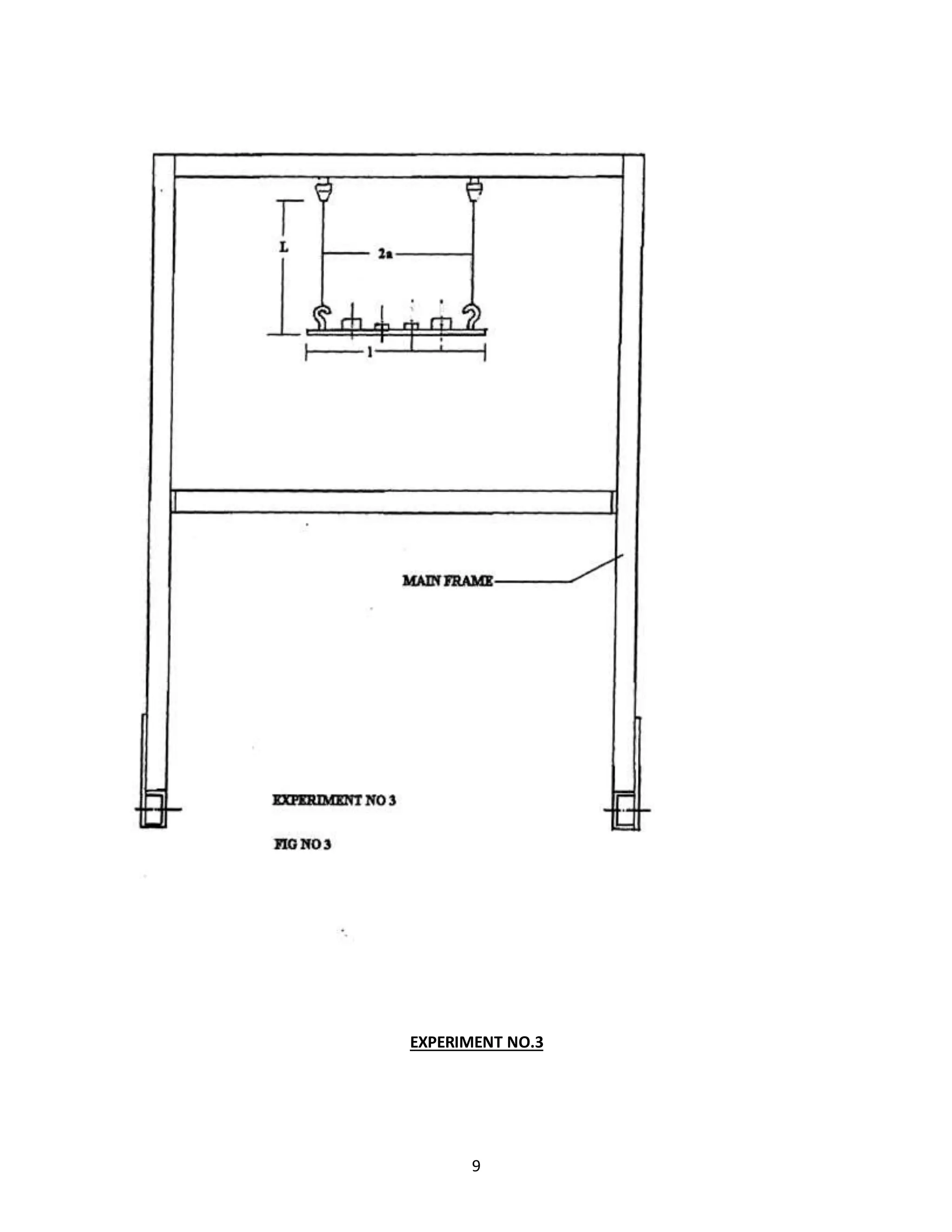
1] Suspendthe bar formhook.The suspensionlengthof each cord mustbe the same.
2] Allowthe barto oscillate aboutthe vertical axispassingthroughthe center&measure the periodic
time‘t’byknowingtime sayfor10 oscillations.
3] Repeatexpt.bymountingthe weightatequal distance formcenter.
4] Complete the observationtable.
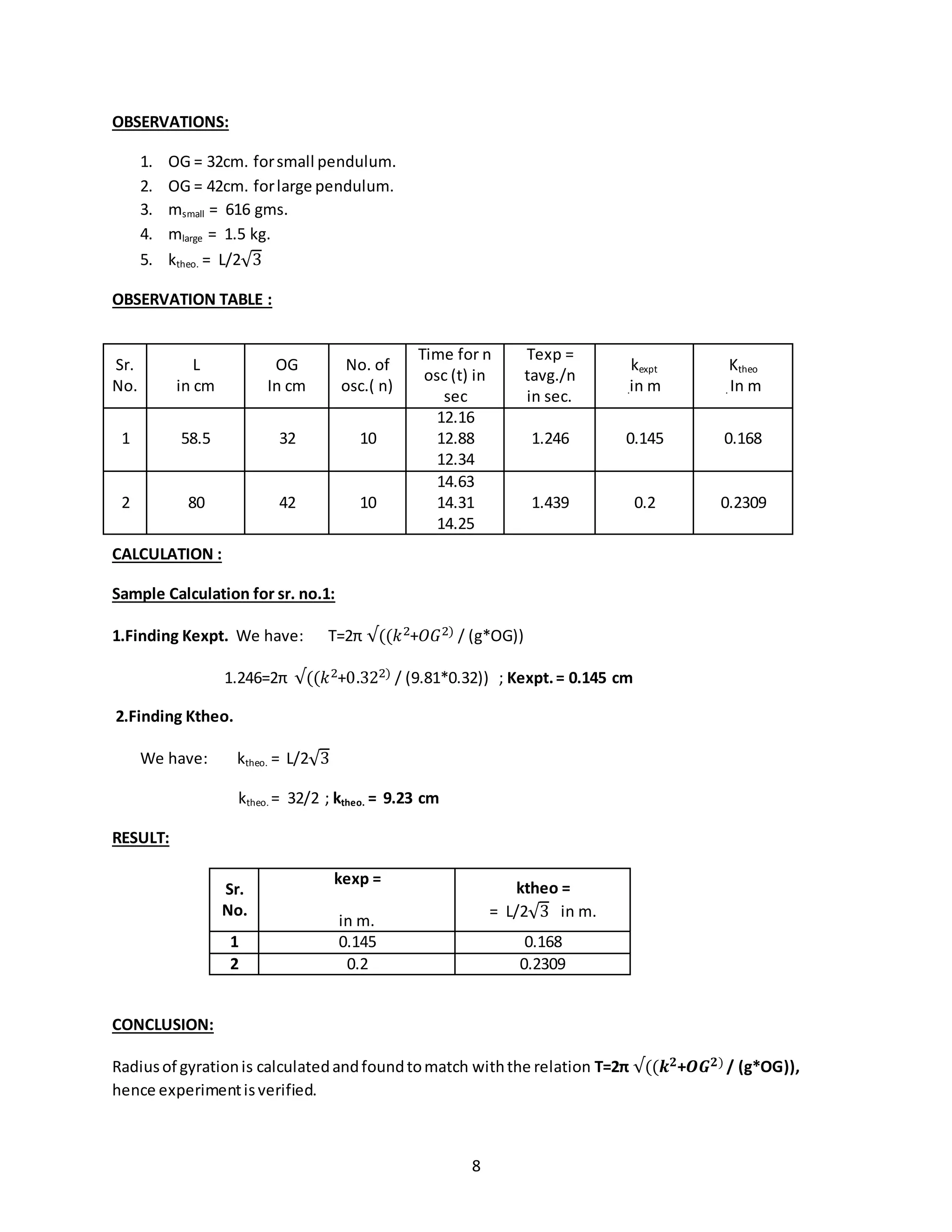
OBSERVATIONS:
Weightonthe platform:800 gms
OBSERVATION TABLE :
Sr.
no.
Wt. on
platform
In gms.
L
In cm
a
in cm
t
in
sec
No. of
oscillations
n
T =
tavg/n
In sec
Kexp.
In cm
ktheo =
= L/2√3
in m.
In cm
1 800 32 43
5.56
5.66
5.91
10 0.571 11.57 9.23
2 2400 32 43
5.56
6.5
6.53
10 0.65 13.23 9.23

13. 13
CALCULATIONS :
Sample Calculation for sr. no.1:
Finding Kexp. T = 2π *(k/a)√(𝒍/𝒈)
0.571 = 2π *(k/23)√(32/9.81)
Kexp. = 11.57 cm
FindingKtheo.
ktheo= L/2√3
ktheo= 32/2√3
ktheo = 9.23 cm
RESULT:
Sr.
no.
Wt. on
platform
in gm
L.
In cm
Kexp.
In cm
Ktheo.
In cm
1 800 32 11.57 9.23
2 2400 32 13.23 9.23
CONCLUSION:
1. As length of cord decreases the radius of gyration decreases.
2. Differencesinthe theoretical ‘k’experimental valuesof ‘k’are due to error in nothing down the
time period.

14. 14
EXPERIMENT NO.4

15. 15
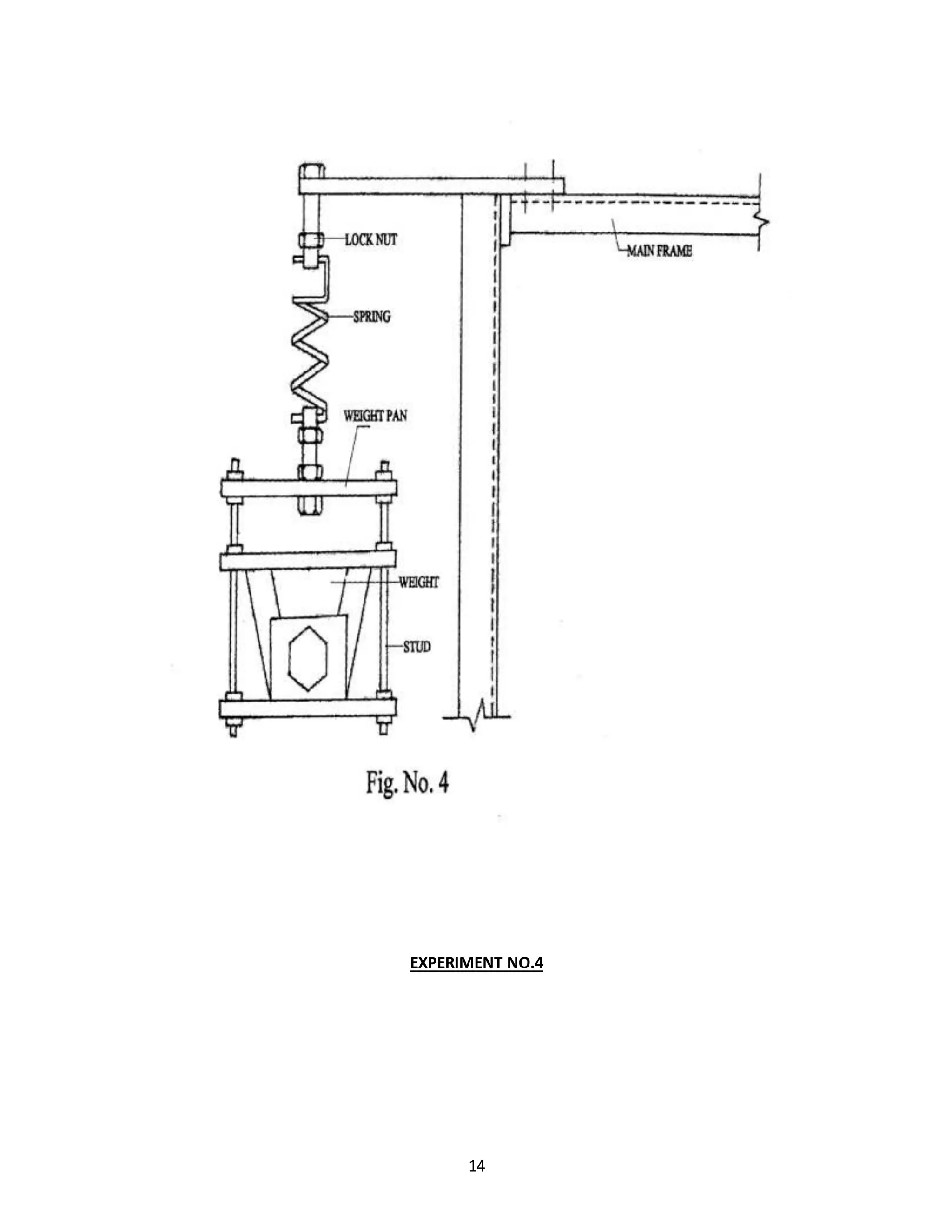
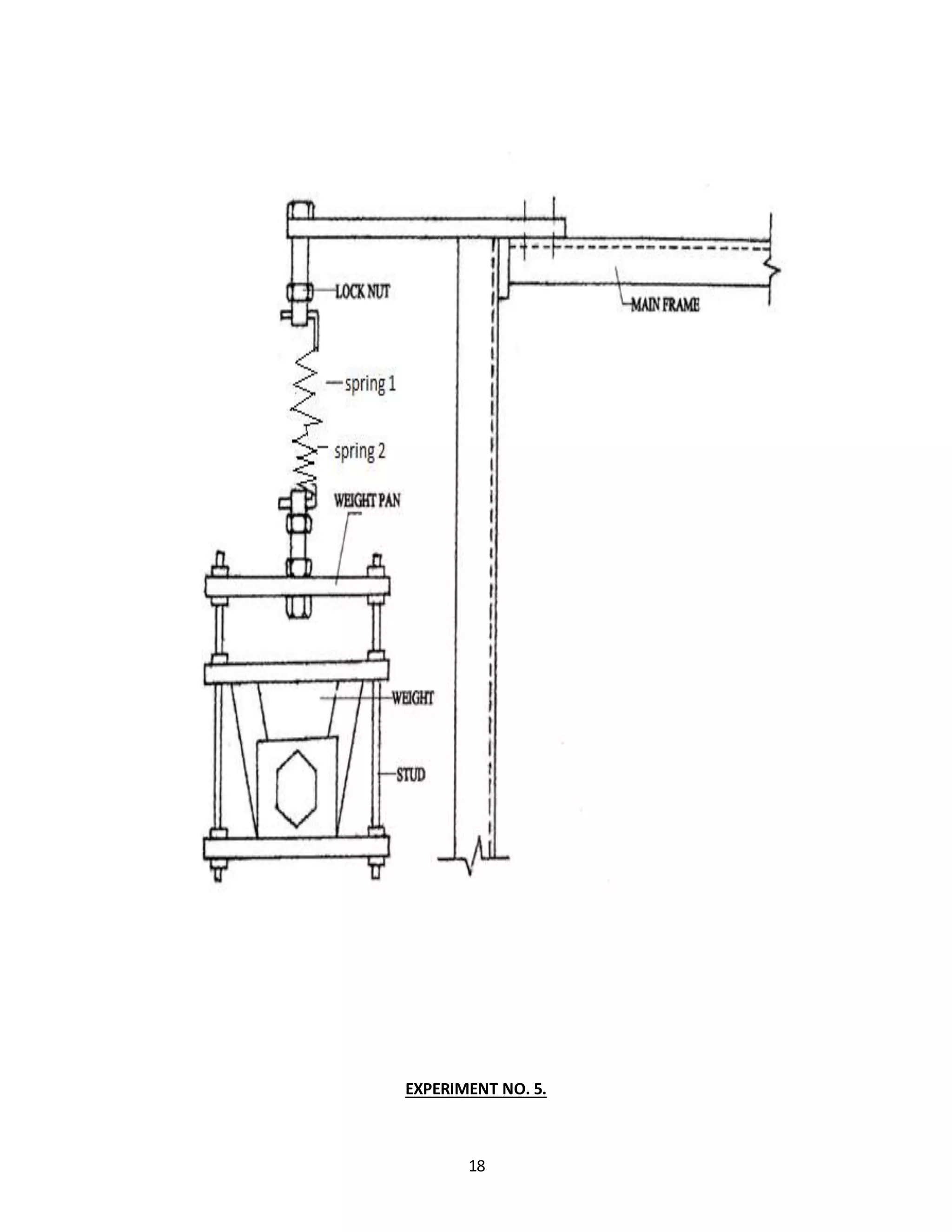
Experiment No 4
LOGITUDINAL VIBRATION OF HELICAL SPRING
AIM:
To studythe longitudinal vibrationof helical springandtodetermine frequencyorperiodof vibration
(oscillation) theoreticallyandactuallybyexperiment.
DESCRIPTION OF SET UP :
One endopencoil spring isfixedtothe screw can be adjusted vertically in any convenient position and
then clamped to upper beam by means of lock nuts. Lower end of spring is attached to the platform
carryingweights. Thus design of system incorporates vertical positioning of the unit to unit to suit the
convenience.
PROCEDURE:
1] Fix one end of vertical spring to the upper screw.
2] Determine free length.
3] Put same weight to platform and down deflection.
4] Stretch the spring through some distance & release.
4] Count the time required (in sec) for some say 10,20, oscillation.
5] Determine the actual period.
6] Repeat the procedure for different weight.

16. 16
OBSERVATIONS:
Weightonthe platform:800 gms
OBSERVATION TABLE 1 :
Spring no. Wt attached (kg)
Deflection of spring
In cm (ᵟ)
K = W/ᵟ
In kg/cm
1 6 1.5 4
2 6 11.5 0.5
OBSERVATION TABLE 2
Spring no. Obs. No.
Wt attached
W in Kg
No. of
oscillations
n
Time
required for
n oscillation
sec
Periodic
time Texpt
=tavg/n in
sec.
Ttheo
In sec
1
1 3 10
2.47
2.53
2.32
0.243 0.174
2 6 10
3.37
3.19
3.06
0.3 0.246
2
1 3 10
5.32
5.30
5.285
0.525 0.4916
2 6 10
6.97
7.03
6.88
0.69 0.695
CALCULATIONS:
Sample Calculation for sr. no.1:
1.Finding K
K = W/ᵟ
K = 6/1.5
K = 4 kg/cm
2.Finding Ttheo.;
Ttheo = 2π √ 𝑤/ km*g

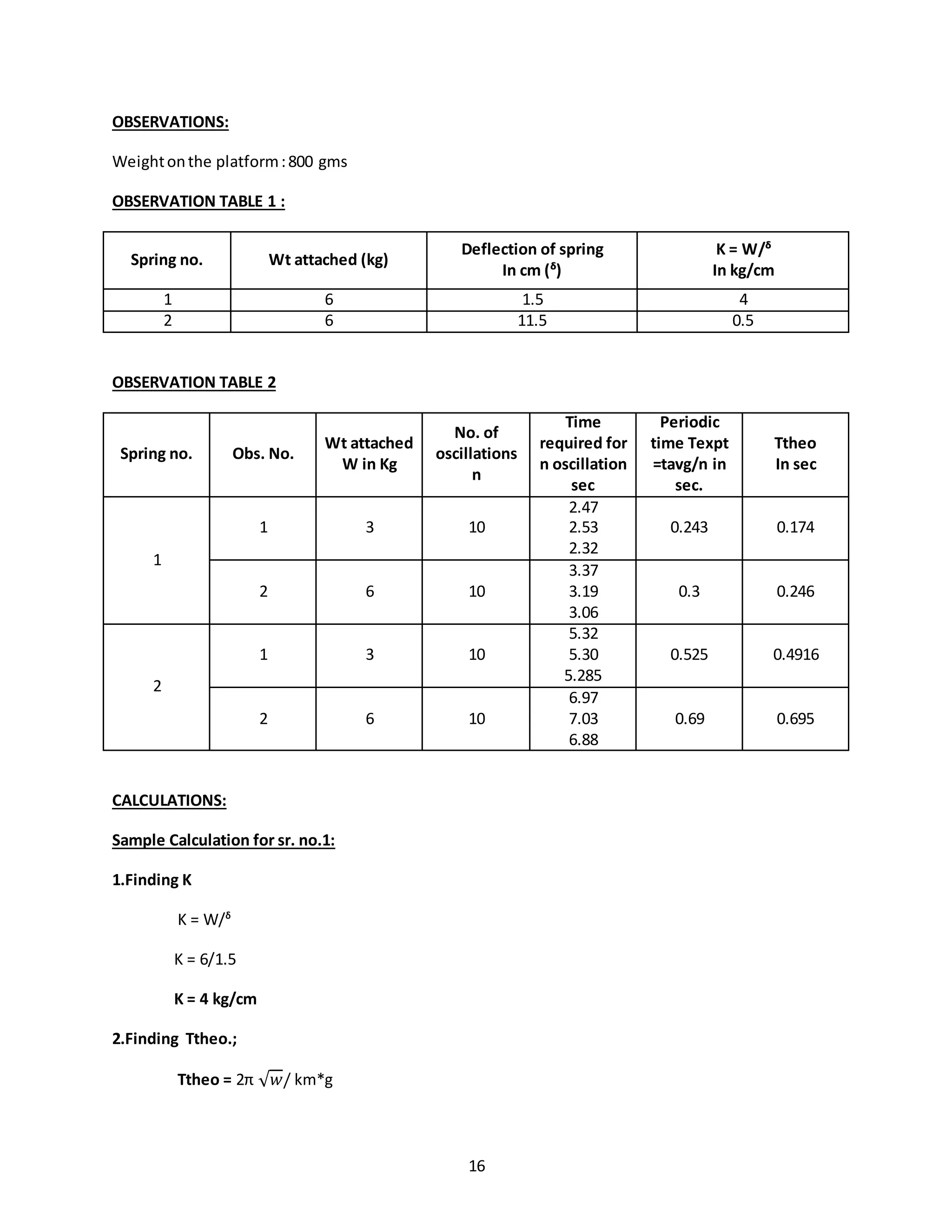
17. 17
Ttheo = 2π √3/ 4*9.81
Ttheo = 0.174 sec.
3.Finding ftheo. and fexpt..;
ftheo. = 1/ Ttheo
ftheo. = 1/ 0.174
ftheo. = 5.74 cps
fexpt. = 1/ Texpt
fexpt. = 1/ 0.243
fexpt. = 4.115cps
RESULT:
For Spring wt.in kg Experimental Theoretical
F in cps F in cps
1 3 4.115 5.74
2 6 3.33 3.33
3 3 1.904 1.904
4 6 1.449 1.449
CONCLUSION:
The difference in F expt & F theoretical is due to
1] Observation human error
2] Damping effect of air.

18. 18
EXPERIMENT NO. 5.

19. 19
Experiment No 5.
Springs in Series
AIM:
To studythe vibrationof systemhavingspringinseries.
DESCRIPTION OF SET UP:
Fig.showsthe general arrangementof experiment setup. It’s consist of fixed support of which there is
hole where spring can be attached through the hook.
THEORY:
SpringinSeries:
Let Ke =Equivalentstiffnessof system
K1,K2 =Deflectionof spring.
The total definitionof the systemisequal tothe sumof deflectionof individual springs.
X =X1 + X2 +X3 +-----
1
𝐾𝑒
=
1
𝐾1
+
1
𝐾2
+
1
𝐾3
+ ------------
Thus the springsare connectedinseriesthe reciprocal of equivalentspring stiffnessisequal tothe sum
of reciprocal of individual springstuffiness.
PROCEDURE:
1. firstthe tensionspring isattachedisattachedto the support with load no attached to it and it’s
length is measure (pitch).
2. Then dead wt is attached to that spring with the help of hook and again length is measured.
3. Same procedure is applied for the spring 2 of different stiffness.
4. Thenspring i.e spring1 andspring2 connectedin series and length is measured then dead wt.
is attached to spring and length is measured.
Observations:
For Spring 1:
Initial pitch= 8mm
Final pitch (withload) =11mm Load = 1.5kg
Deflection =3mm

20. 20
For Spring 2:
Initial pitch= 7mm
Final pitch (withload) =8.5mm Load = 4.872kg
Deflection=1.5mm
For Springs in series:
Initial length=24cm
Final length(withload)=27.8cm Load = 1.5kg
Deflection=3.8cm
CALCULATIONS:
For Spring 1:
K1 = Load*9.81/defn
K1 = 1.5*9.81/0.003
K1 = 4905 N/m
For Spring 2:
K2 = Load*9.81/defn
K2 = 4.872*9.81/0.0015
K2 = 31862.88 N/m
For Springs in series:
Kexpt= Load*9.81/defn
ωnexpt = √Kexpt /m
Kexpt= 1.5*9.81/0.038 ωnexpt = √3872.4 /1.5
Kexpt=3872.4 N/m ωnexpt = 50.8 rad/sec.
1/Ktheo= 1/k1 +1/k2 ωnexpt = √Kexpt /m
Ktheo = 4250.65N /m ωnexpt = 53.28 rad/sec.

21. 21
RESULT:
Kexp =3872.4 N/m , Wexp = 50.81 rad/sec
K th = 4250.66 N/m, W th = 53.28 rad/sec
CONCLUSION:
The theoretical and experimental value of equivalent stiffness were found to almost equal.

22. 22
Experiment No 6.

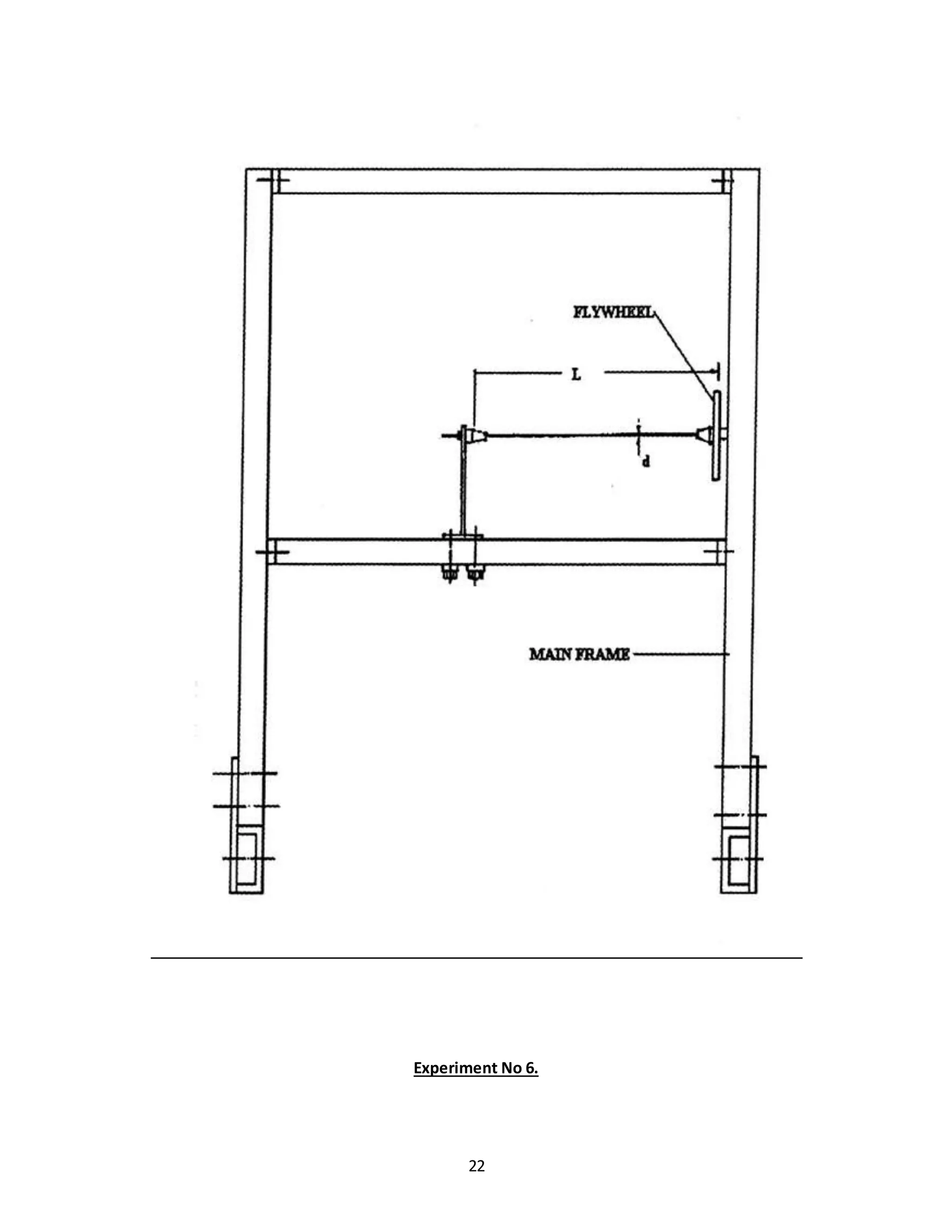
23. 23
Experiment No 6.
UNDAMPED TORSIONAL VIBRATION OF SINGLE ROTOR SHAFT SYSTEM
AIM: To studyundampedtorsional vibrationof singlerotorshaftsystem.
DISCRIPTION OF SET UP:
The arrangementisan showninfigone endof shiftisgrippedindule anda flywheel freetorotate in
ball bearinginfixedtootherendof shaft.
The bracket withfixedendshaftcanbe convenientlydampedatanypositionalongbeam.Thuslengthof
shaftcan be variedduringexperiment,especiallydesigned b chucks are used for clamping end of shaft.
The ball bearingsupportto flywheel providesnegligible acting support during experiment. The bearing
housing is fixed to side member of main frame.
PROCEDURE:
1] Fix bracketat convenientpositionalongleverbeam.
2] Grip one endof shaftat bracketby meansof chucks.
3] Fix rotor ontothrough endof shaft.
4] Twistthe rotor through semi cycle andrelease.
5] Note downtime requiredfor10 oscillations.
6] Repeatprocedure fordifferentlengthof shaft.

24. 24
Putting IP =2.513*0.001, G = 800000 Kg/cm2
, L =52.5 cm

25. 25

26. 26
Experiment No 7.

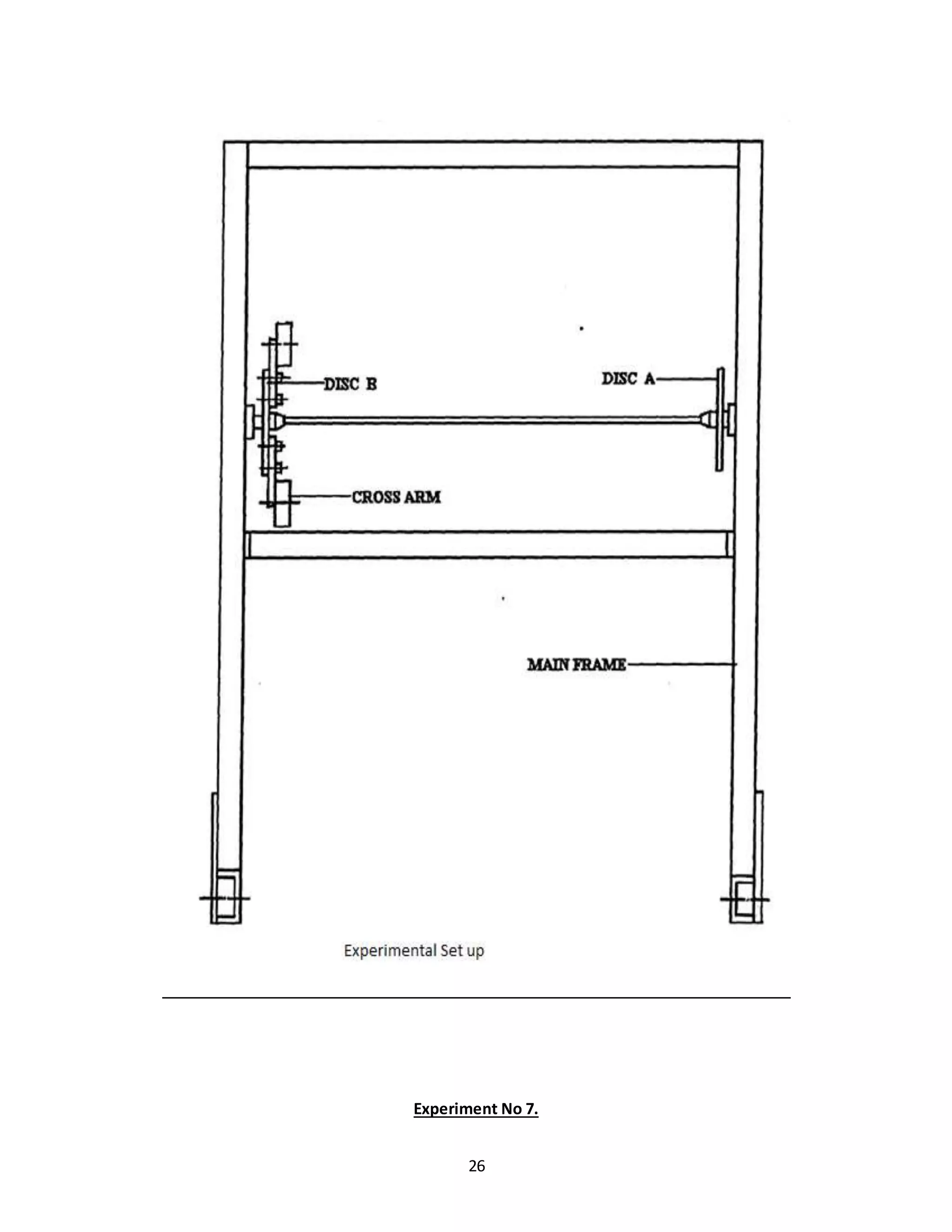
27. 27
Experiment No 7.
TORSIONAL VIBRATION OF DOUBLE ROTOR SYSTEM
AIM: To studytorsional vibrationof adouble rotorshaftsystem.Andtodetermine theoretical and
experimental value of natural frequency.
DISCRIPTION OF SET UP:
The arrangementisanshownin fig.Two discshavingdifferentmassmomentof inertiaare clampedone
at each endof shaft bymeansof colletandchucks.MassMomentof inertiaof anydisccan br changed
by attachingthe cross leverweights.BothDiscsare free tooscillate inball bearings.This provides
negligible dampingduringexperiment.
PROCEDURE:
1] Fixedtwodiscsto the shaftsandfit the shaftinbearing..
3] Apply angularmotiontotwo discsinopposite direction byhandandreleased.
4] Measure the oscillationof the periodfornno. of oscillations.
5] Fit the cross arm to one of the discssayB and againnote downtime.
6]Repeatthe peocedure withdifferentmassesandnote downtime.

28. 28

29. 29

30. 30
CONCLUSION:
Differentinpractical andtheoretical timeperioddue to
1] Human error
2] Dampingfactor
3] Slip

31. 31
Experiment No .8

32. 32
Experiment No .8
UNDAMPED FREE VIBRATION
TITLE:
To studythe undampedfree vibrationof equivalentspringmasssystem.
DESCRIPTION OF SETUP:
The arrangementisshowninfig.it isdesignedtostudyfree forceddamped and undamped vibration. It
consists of MS rectangular beam supported at one end by. Trunninion private in ball bearing. The
bearinghousingisfixedtothe side memberof the frame.The otherendof the beamis supportedtothe
lower end of helical spring. Upper end of spring is attached to the screw.
The exciterunitcanbe mountedat anypositionalongthe beam.Additional knownweightmaybe
addedto the wt platformunderside the exciter.
THEORY:
Kineticenergyof the system=Kineticenergyof equivalent system.
∑((1/2)Mi(dxi/dt)2
)=(1/2)Me(dxe/dt)2
-------------(1)
From fig,we have
Xi=Li(dӨ/dt)andXe=Le(dӨ/dt).
Equation(1) become,
∑((1/2)MiL12
(dӨ/dt)2
=(1/2)MeLe2
(dӨ/dt)2
Me=∑mi(Li/Le)2
Here. Mi=M+M.
AndLi=L1=L

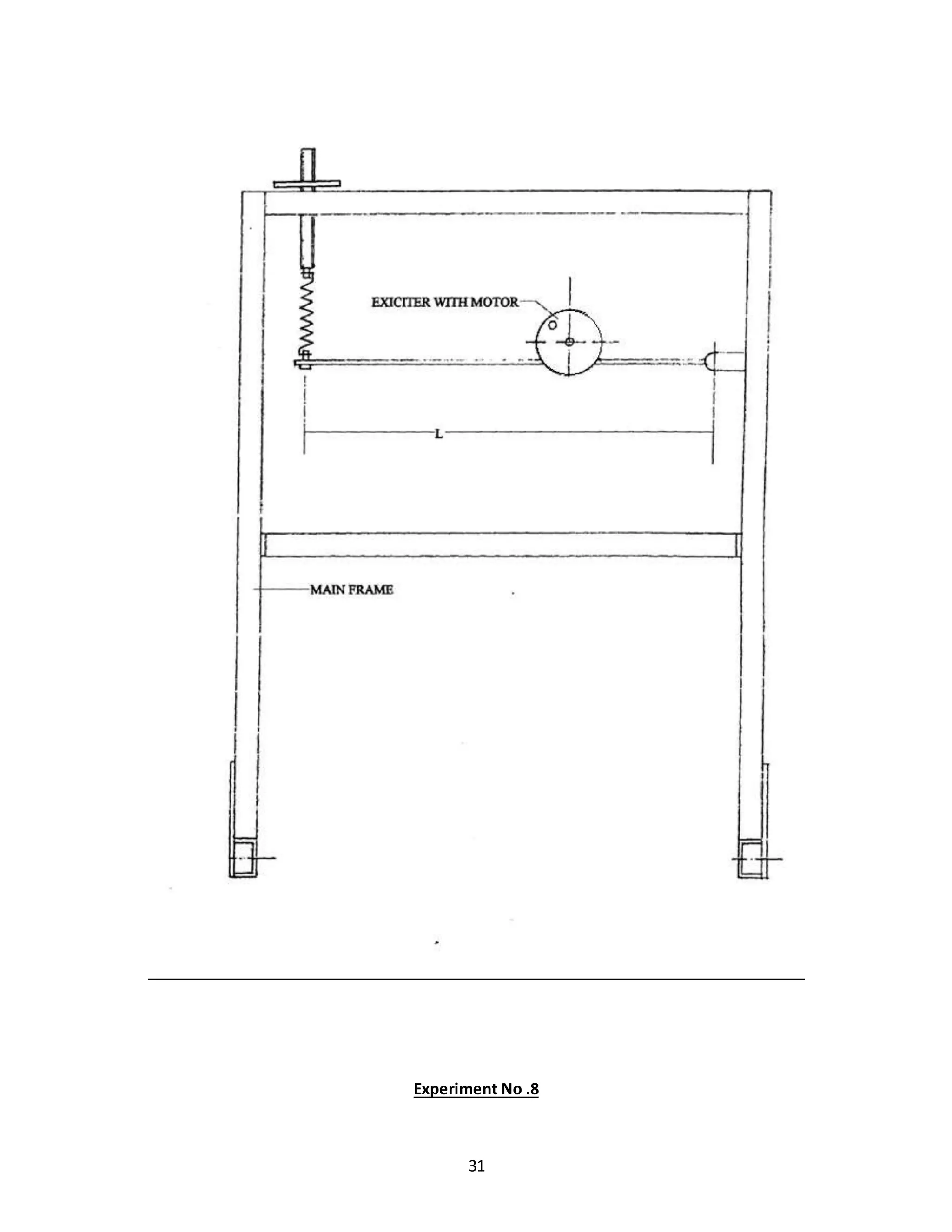
33. 33
Meq=(M+M)*(L1/L)2
Andnowdoingsimilaranalysisasinabove analysis.
PROCEDURE:
1] Supportone endof the beamin the slatof trunionand clampit by a meansof screw.
2] Attach the otherendof beamto the lowerendof spring.
3] Adjustthe screwto whichthe springisattached. Such that the beamis horizontallyinthe above
position.
4] Weightthe exciterassembly alongwithdisc&bearingendweightplatform.
5] Clampthe assemblyatany convenientposition.
6] Measure the distance L1 of the assemblyfromprivate.
7] Measure the time forany IOsecandfindthe periodictime andnature frequency.
8] Repeatthe experimentbyvaryingL1and by pottingdifferentweightonthe platform.

34. 34
CONCLUSION: Undamped vibrations of equivalent spring mass system was studied.

35. 35
Experiment No 09

36. 36
Experiment No 09.
FORCED VIBRATION
TITLE: -
To studythe forcedvibrationof equivalentspringmasssystem.
DESCRIPTION OF SET UP :-
The arrangementisshowninFig.It is similartothatdescribedforexpt.No.8.The exciterunitiscoupled
to D.C. variable speedmotor.
Speedof the motorcan be variedwiththe dimmerstatprovidedonthe control panel.Speedof rotation
can be knownfromthe speedindicationonthe control panel.Itisnecessarytoconnectthe damperunit
to the exciter.Amplituderecordof vibrationistobe obtainedonthe strip-chartrecorder.
PROCEDURE:
1. Arrange the set-upasdescribedforexpt.no.8.
2. Start the motor& allowthe systemtovibrate.
3. Wait for 1 to 2 minutesforthe amplitude tobuildthe particularforcingfrequency.
4. Adjustthe positionof strip-chartrecorder.Take the recordof amplitude vs.time onstrip- chartby
startingrecordingmotor.Pressthe recorderplatformonthe pengently.Penshouldbe wetwithink.
Avoidexcessive pressure togetgoodrecord.
5. Take recordby changingforcingfrequency.
6. Repeatthe experimentfordifferentdamping.Dampingcanbe changedby adjusting the holesonthe
pistonof the damper.

37. 37
CONCLUSION: Forced vibrations of equivalent spring mass system was studied.

38. 38
Experiment No 10.

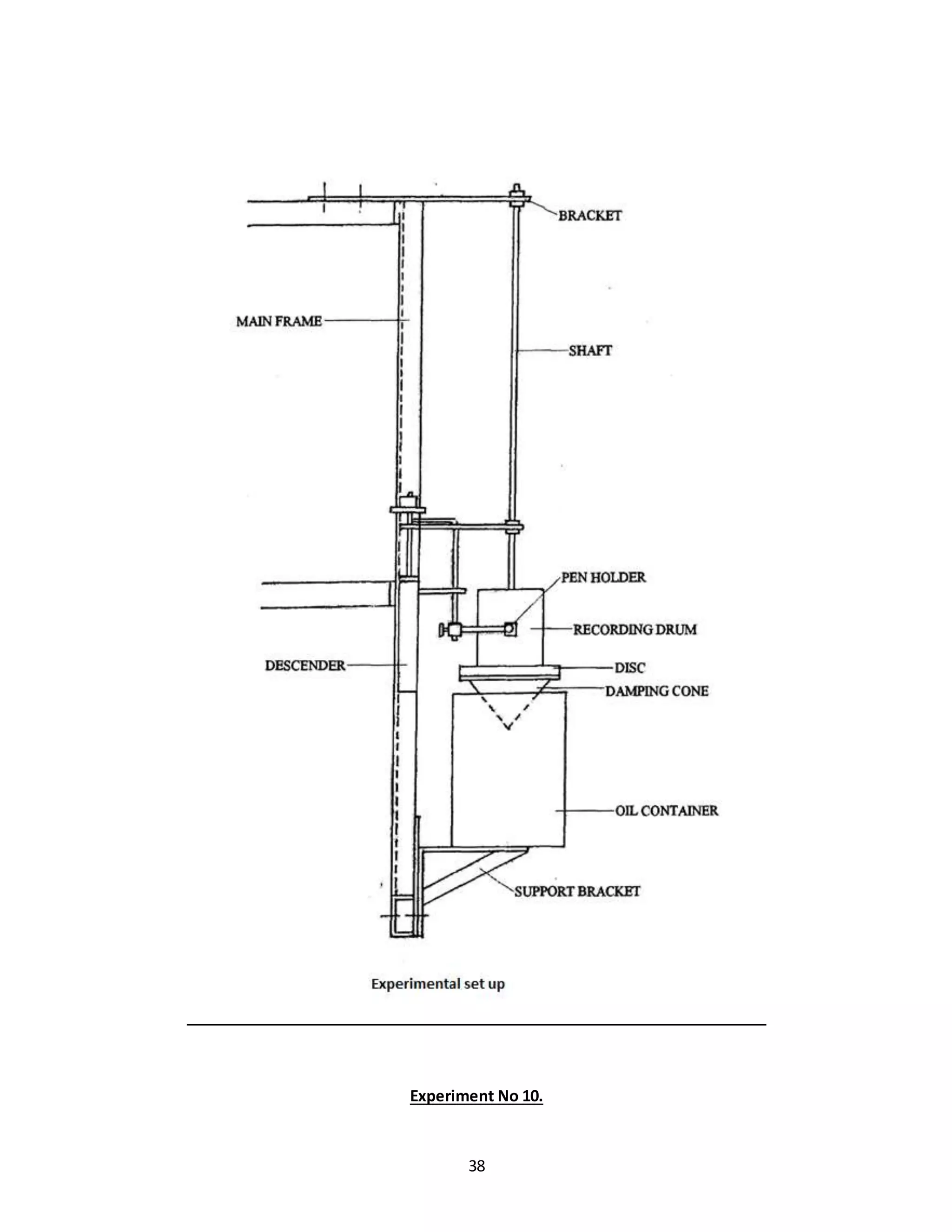
39. 39
Experiment No 10.
DAMPED TORSIONAL VIBRATION
AIM:
To study damped torsional oscillation and determine damping coefficient.
DESCRIPTION OF SET UP:
The fig showsgeneral arrangementforexperiment.Itconsistsof longelasticshaft gripped at upper end
by chuckin bracket.The bracket isclampedtoupperbeamof mainframe.A heavyflywheel Clamped to
lowerendof shaft suspended frombracket,thisdrumisimmersedinoil whichprovides damping. Rotor
can be takenupand downfor varyingdepthof immersionof dampingdrum,depthof immersion can be
read on scale.
PROCEDURE:
1] With no container allow flywheel to oscillate and measure time for 10 Oscillations.
2] Put thin mineral oil in drum and note depth of immersion.
3] Allow flywheel to vibrate.
4] Put sketching pen in bucket.
5] Allow pen to descend see that pen always makes contact with paper and record oscillations.
6] Measure time for some oscillations by means of stop watch.
7] Determine amplitudes of any positions.
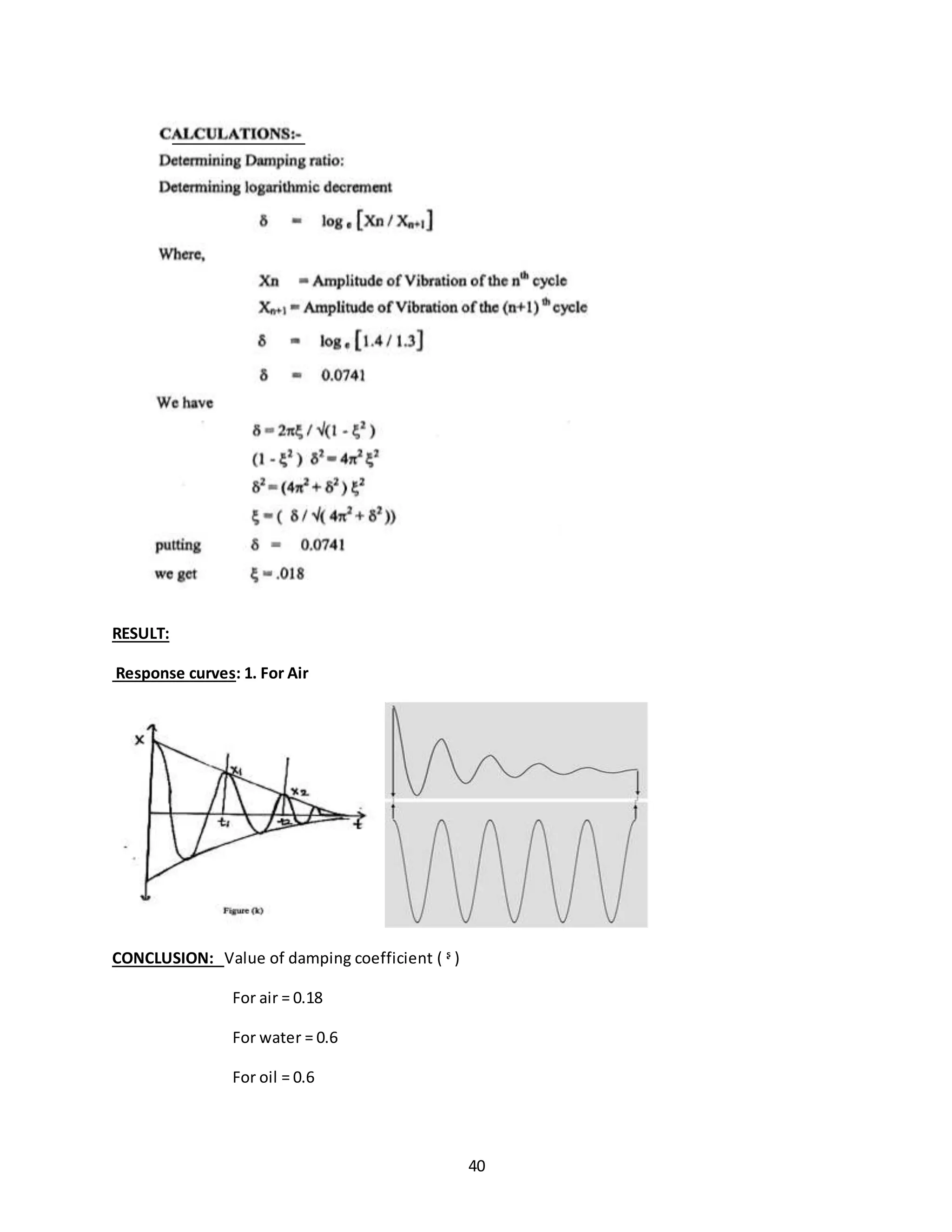
OBSERVATION TABLE:
Sr.
no.
Damping medium Xn Xn+1
1 Air 1.4 1.3
2 Water 1.15 0.6
3 Oil 1 0.6

40. 40
RESULT:
Response curves: 1. For Air
CONCLUSION: Value of damping coefficient ( ᶳ )
For air = 0.18
For water = 0.6
For oil = 0.6

41. 41
Experiment No 11.

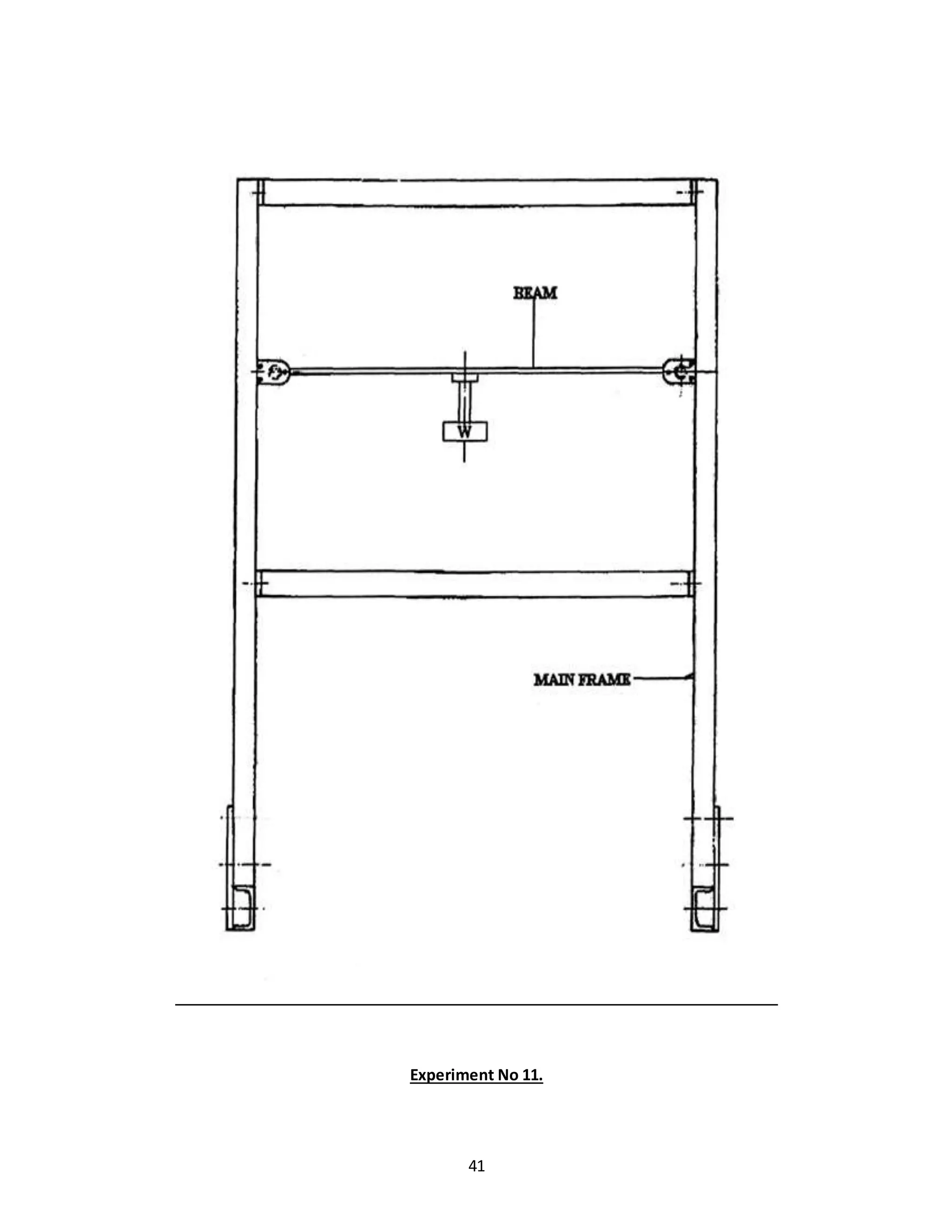
42. 42
Experiment No 11.
DUNKERLEY’S RULE
AIM:
To verifyDunkerley’s
1
𝐅^𝟐
+=
1
𝐅𝐋^𝟐
+
1
𝐅𝐁^𝟐
Where F = Natural frequencyof beamwithcentral loadw.
FL=Natural frequencyof givenbeamwithcentral loadtobe calculatedas:
Fb =√
48𝐸𝐼𝑔
4𝑊𝜋^2𝐿^3
L = Lengthof beam
W = Central Load.
Fb =Natural Frequency
DISCRIPTION OF SET UP:
The fig showngeneral arrangementforcarryingexperimenta rectangular beam supported on a trunion
at each end ,each trunion is pivoted on ball burning carried in housing & is fixed to vertical frame
member. The beam carries at its center a weight platform
.
PROCEDURE:
1] Arrange the setup as shown with some weight W clamped to weight platform.
2] Pull the plat form and release it to set the system into natural vibration.
3] Find the periodic time T and frequency of vibration by measuring time for some oscillation.
4] Repeat expt by additional mass on weight platform.

43. 43
OBSERVATIONS:
1.Length of beam = 1035 mm
2.Sectional area of beam = (25*6) mm2
3.Weight of the beam =1.215 kg
4.wt per cm of beam weight = w/l = 1.1739 kg/m.
OBSERVATION TABLE:
SR.
NO.
Wt. attached
W in kg
No.of oscillations
n
Time for n
oscillations t in
sec
T = tavg/n
In sec.
1/F2
1 1.5
5
5
5
0.9
0.92
0.96
0.18
0.184
0.192
0.0324
0.0338
0.0368
CALCULATIONS:
1. Texpt = t/n = 0.9/5 =0.18 sec.
2. Fexpt. =1/Texpt = 1/ 0.18 = 5.55 Hz
3. Fb2
= 𝜋/2L2 *
√ 𝐸𝐼𝑔/𝑤^2
W = 1.173 kg/m
I = bh3
/12 = 450*10^-12 m4
E = 2*10^10 Kg / m2
4. FL =√
48𝐸𝐼𝑔
4𝑊𝜋^2𝐿^3
= 8.034 Hz
5. By Dunkerley’s formulae
1
𝐅^𝟐
+=
1
𝐅𝐋^𝟐
+
1
𝐅𝐁^𝟐
, = 0.022 Hz
RESULT:
Sr No Dead Wt attached 1/F2
experimental 1/F2
theorotical
1 1.5 0.0324 0.022
CONCLUSION:
Thus Dunkerley’srule isverified ,since theoretical andexperimental valuesare closer.

44. 44
Experiment No 12.
STATIC AND DYNAMIC BALANCING
AIM : To calculate the orientationandlongitudinal positionof balancingmassesof amulti-rotorsystem
so that itis balancedstaticallyanddynamicallyandcheckitexperimentally.
GIVEN:
Two massesm1 and m2 are spaced10cm apart ona shaftand massm2 isorientedat90° withrespectto
mass m.
PROBLEM STATEMENT:
To locate orientationandpositionof balancingmassm3 andm4 so that rotatingmassessystemis
balanced.
DESCRIPTION OF SET UP:
A Steel shaftismountedinball bearingatitsends,are housedina rectangularmainframe . Adisc
carryinga circularportionand protractionscaleandpointerisprovidedatendof the frame for angular
adjustmentof the massesonthe shaft.The masses can be attached anddetachedandslide overthe
shaft.The positionof the massescan be adjustedwiththe helpof ascale at the bottomof the frame
and a sittingguage whichcan move overthe scale to helplocate the masses.
PROCEDURE:
1.STATIC BALANCING:

45. 45
Remove the drive belt.Unlockthe frame fromchaintoclamp itto the main frame at itstop , bymeans
of nut andboltarrangement.The value of (m-r) foreachblockisdeterminedbyclampingeachblockin
turn of shaft.
Here,m = massof block
r = eccentricity of c.g of block from the axis rotation.
Moment due towt. Of steel bolts = Moment due to wt. of block
FOR STATIC BALANCING, Σmω2
r = 0
2.DYNAMIC BALANCING:
Keep system idle with no vibration, Using value of (mr ) for each block draw force and couple polygon
from given data.
OBSERVATION TABLE:
R.P BLOCK PHASE FORCE VECTOR
mr=n
DIST. OF MASS
FROM R.P in m (x)
COUPLE VECTOR
mrx
1 mc1 37 0 0
2 mA 45 4.5 202.5
3 mB 50 9.5 47.5
4 mc2 31 18 558

46. 46
CALCULATIONS:
1.COUPLE POLYGON:
mA.rA.xA= 202.5, ΘA = 0°
mB.rB.xB= 475, ΘB = 90°
From graph,
mc2.rc2.lc2 = 550
mc2.rc2.50 = 550
mc2.rc2 =31
2.FORCE POLYGON:
mA.rA.= 45, ΘA = 0°
mB.rB= 50, ΘB = 90°
From graph,
mc2.rc2. = 31 , Θc2 = 235°
RESULT:
Mass m Angle of
orientation w.r.to
x-axis
mr=n = no. of balls POSITION OF
MASSES FROM
R.P in m (x)
mc1 0 37 0
mA 90 45 4.5
mB 215 50 9.5
mc2 236 31 18

47. 47
CONCLUSION:-
The orientationandpositionof balancing masses been calculated as shown above. Based upon results
the experimenthasbeencalculatedanditisfoundthatframe doesnot vibrate while shaft rotates have
that these is no reduction set up at the bearing and hence unbalanced masses are balanced statically
and dynamically.