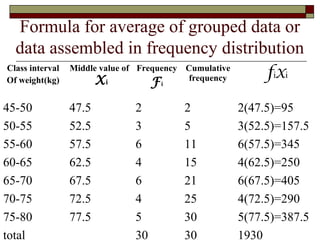
This document discusses various measures of central tendency including the mean, median, and mode. It provides definitions and formulas for calculating each measure. The mean is the average and is calculated by summing all values and dividing by the total number of data points. The median is the middle value when data is arranged in order. The mode is the value that occurs most frequently in the data set. Examples are given to demonstrate calculating each measure. The document also discusses advantages and limitations of each central tendency measure.

1. CENTRAL TENDANCY
DR DIGVIJAY R PARMAR

2. BIOSTATISTICS
 Statistics is the science of the collection,
organization, and interpretation of data.
 Biostatistics (a contraction of biology and
statistics; sometimes referred to
as biometry or biometrics) is the application
of statistics to a wide range of topics in biology.

3. INTRODUCTION
 Classification of data are helpful in reducing
and understanding the bulk of the large mass
data.
 But they are descriptive.
 So need arises,to find a constant which will be
representative of a group.

4.  MEASURES OF CENTRAL TENDANCY
OR AVERAGE
 MEASURES OF VARIATION
 MEASUREA OF SKEWNESS AND
KURTOSIS

5. Different measures of central tendency
1. Mean : 1. Arithmetic mean
2. Harmonic mean
3. Geometric mean
2. Median :
3. Mode:
4. Quantiles:1.quartiles
2.deciles
3.percentile

6. AVERAGE
 By careful observation of data, it can be
noticed that observations tend to cluster
around central value.
 This is called central tendency of that group.
 This central value is known as a average.

7. The Mean
 The most commonly used
measure of central tendency is
called the mean ( denoted
for a sample, and µ for a
population )
 The mean is the same of what
many of us call the ‘average’,
and it is calculated in the
following manner .
X
Population
Sample
x
N
x
x
n
µ =
=
∑
∑

8. Arithmetic mean
 It is commonly used measure of central
tendency.
 It is sum all observations divided by number
of observations

9. For ungrouped data
 Mean of ‘n’ observations x1,x2…….xn is
given by
 A.M.= X1+X2+…….+Xn
n
= sum of observations
Number of observations

10. Example:-
 61, 58, 62, 67, 65, 68, 70, 69.
 Weight of 8 people
X=61+58+62+67+65+68+70+69
8
= 520
8
= 65

11. MERITS OF A.M.
 it is easy to calculate and understand.
 it is based on all observations.
 it is familiar to common man and rigidly defined.
 it is capable of further mathematical treatment.
 it is least affected by sampling fluctuations hence
more stable.

12. DEMERITS OF A.M.
 Used only for quantitative data not for
qualitative data like caste, religion, sex.
 Unduly affected by extreme observation.
 Can’t be used open ended frequency
distribution.
 sometimes A.M may not be an observation in
data.
 Can’t be determined graphically.

13. GEOMETRIC MEAN(GM)
 When data contains few extremely large or small
values in such case arithmetic mean is unsuitable
for data
 GM of n observation is defined as ‘n’th root of the
product of n observation.
 Simple arithmetic mean of the logarithmic value of
individual values.
 logarithmic value of this log is the geometric mean

14. HARMONIC MEAN:
 It is reciprocal of arithmetic mean of
reciprocal observations.

15. FOR THE NUMERICAL VALUES OF 1,2,3,4,5, CALCULATE
AND COMPARE THE AM , GM , HM .
 AM = 1+2+3+4+5 = 15 = 3.0
5 5
GM = 1/5(log1+log2+log3+log4+log5)
= 1/5(0+0.3010+0.4771+0.6020+0.6989)
= 1/5(2.07918) = 0.415836
= antilog 0.415836 = 2.60517
HM = 1 = 5 =2.242
1/5(1/1+1/2+1/3+1/4+1/5) 2.23

16. The Median
Median Location = N + 1
2
 The median is the point corresponding to the score that lies in
the middle of the distribution ( i.e., there are as many data
points above the median as there are below the median ).
 To find the median, the data points must first be sorted into
either ascending or descending numerical order.
 The position of the median value can then be calculated using
the following formula:

17. EXAMPLE
 MedianMedian – the middle number in a
set of ordered numbers.
4, 5, 6 ,7,8
Median = 6Median = 6

18. How to Find the Median in a Group of
Numbers
 Step 1 – Arrange the numbers in
order from least to greatest.
21, 18, 24, 19, 27
18, 19, 21, 24, 27

19. How to Find the Median in a Group of
Numbers
 Step 2 – Find the middle
number.
21, 18, 24, 19, 27
18, 19, 21, 24, 27

20. How to Find the Median in a Group of
Numbers
 Step 2 – Find the middle
number.
18, 19, 21, 24, 27
This is your median number.

21. How to Find the Median in a Group of
Numbers
 Step 3 – If there are two middle
numbers, find the mean of these two
numbers.
18, 19, 21, 25, 27, 28

22. How to Find the Median in a Group of
Numbers
 Step 3 – If there are two middle
numbers, find the mean of these two
numbers.
21+ 25 = 46
2)46
23 median

23. What is the median of these
numbers?
16, 10, 7
10
7, 10, 16

24. What is the median of these numbers?
29, 8, 4, 11, 19
11
4, 8, 11, 19, 29

25. What is the median of these numbers?
31, 7, 2, 12, 14, 19
13
2, 7, 12, 14, 19, 31
12 + 14 = 26 2) 26

26. What is the median of these
numbers?
53, 5, 81, 67, 25, 78
60
53 + 67 = 120 2) 120
5, 25, 53, 67, 78, 81

27. Merits of Median
 Like mean, median is simple to understand
 Median is not affected by extreme items
 Median never gives absurd or fallacious
results
 Median is specially useful in qualitative
phenomena

28. Limitations
 It is not suitable for algebraic treatment
 The arrangement of the items in the ascending
order or descending order becomes very
tedious sometimes
 It cannot be used for computing other
statistical measures such as S.D or correlation

29. The Mode
 The mode is simply the value of the relevant variable
that occurs most often (i.e., has the highest
frequency) in the sample
 Note that if you have done a frequency histogram,
you can often identify the mode simply by finding
the value with the highest bar.
 Modes in particular are probably best applied to
nominal data

30. Definition
 A la modeA la mode – the most popular
or that which is in fashion.
Baseball caps are a la mode today.

31. How to Find the Mode in a Group of
Numbers
 Step 1 – Arrange the numbers in
order from least to greatest.
21, 18, 24, 19, 18
18, 18, 19, 21, 24

32. How to Find the Mode in a Group of
Numbers
 Step 2 – Find the number that is
repeated the most.
21, 18, 24, 19, 18
18, 18, 19, 21, 24

33. Which number is the mode?
29, 8, 4, 8, 19
8
4, 8, 8, 19, 29

34. Which number is the mode?
1, 2, 2, 9, 9, 4, 9, 10
9
1, 2, 2, 4, 9, 9, 9, 10

35. Which number is the mode?
22, 21, 27, 31, 21, 32
21
21, 21, 22, 27, 31, 32

36. Mode
 Advantages
 Very quick and easy to determine
 Is an actual value of the data
 Not affected by extreme scores
 Disadvantages
 Sometimes not very informative (e.g. cigarettes smoked in
a day)
 Can change dramatically from sample to sample
 Might be more than one (which is more representative?)

37. Formula for average of grouped data or
data assembled in frequency distribution
Class interval
Of weight(kg)
Middle value of
Xi
Frequency
Fi
Cumulative
frequency fiXi
45-50 47.5 2 2 2(47.5)=95
50-55 52.5 3 5 3(52.5)=157.5
55-60 57.5 6 11 6(57.5)=345
60-65 62.5 4 15 4(62.5)=250
65-70 67.5 6 21 6(67.5)=405
70-75 72.5 4 25 4(72.5)=290
75-80 77.5 5 30 5(77.5)=387.5
total 30 30 1930

38. ARITHMETIC MEAN
1
1
K
i i
i
N
i
i
X f
X
f
=
•
=
=
∑
∑
WHERE Xi = midpoint of the ith class interval
fi = frequency of the ith class interval
N = sum of the frequencies

39. MEDIAN
median = I+N/2-CFxh
f
I = lower boundary of median class
N = total frequency
C.F = less than cumulative frequency of the class
preceding the median class
f = frequency of median class
h = class width

40. MODE
Mode =I+(Fm-F1)h
2Fm-F1-F2
Where,
I=lower boundary of modal class
Fm =frequency of modal class
F1 =frequency of pre modal class
F2 =frequency of post modal class
h =width of modal class

41. •THERE ARE TWO CLASS INTERVALS WITH MAXIMUM FREQUENCY
•THEY ARE 55-60 AND 65-70.
So for first time, l = 55 , fm = 6 , f1 = 3 , h = 5 , f2 = 4
now substituting these values , we get
1 st mode = 55 + (6-3)5 =55 +3 = 58
12-3-4

42. RULES OF THUMB
“ALWAYS USE MEAN UNLESS IT IS
CONTRAINDICATED.MEAN IS CONTRAINDICATED
WHEN ETREME VALUES ARE PRESENT.IN A RARE
CASE WHEN INTEREST IS SPECIFICALLY IN
MOST COMMON VALUE, USE MODE. IT MAY BE
ADDED AS A PASSING REFERENCE THAT , FOR A
SET OF DATA , MEAN AND MEADIAN ARE
UNIQUE, i.e. THERE IS ONLY ONE VALUE
ASSOCIATED WITH THESE MEASUREA ,BUT
MODE CAN BE MORE THAN ONE.”

43.  HAVE
A
NICE
DAY!