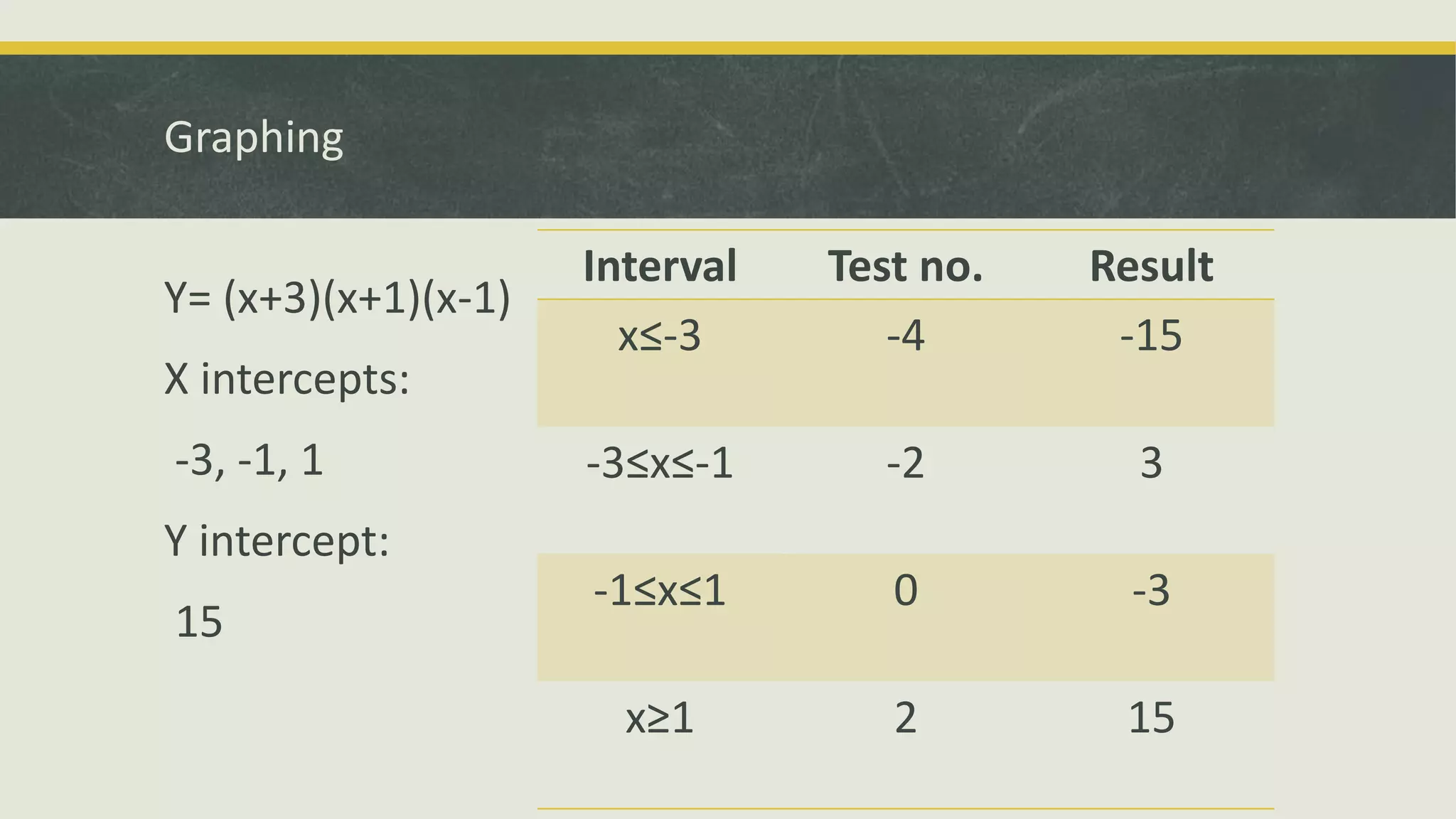
The rational root theorem states that if P/Q is a rational root of a polynomial equation with integer coefficients, then P must be a factor of the leading coefficient and Q must be a factor of the constant term. The document also discusses using the interval test and graphing polynomials to determine where a polynomial is positive or negative. It provides examples of sketching graphs of polynomials based on their degree and characteristics at roots, such as whether the graph will cross or bounce at roots depending on if the root's multiplicity is odd or even.

1. Rational Root Theorem

2. What is the rational root theorem?
The polynomial equation is p(x)=0 has integral
coefficients. If P/Q is a rational root of the polynomial
equation. Then P is a factor of Ao and Q is a factor of
An (leading coefficient)

3. P: +1, -1, +3, -3
Q: +1, -1, +2, -2
P/Q: +1, -1, +3, -3, +1/2, -1/2, +3 2, -3/2

4. Polynomial Inequalities
1. x3
− 3x2
- x- 3 ≥ 0
(x+3)(x+1)(x-1)
Critical Numbers: -3, -1, 1
Conclusion : -3≤x≤-1 OR x≥1

5. How?
Interval Test No. Result Yes or No
x≤-3 -4 -15 No
-3≤x≤-1 -2 3 Yes
-1≤x≤1 0 -3 No
x≥1 2 15 Yes

6. Graphing
Y= (x+3)(x+1)(x-1)
X intercepts:
-3, -1, 1
Y intercept:
15
Interval Test no. Result
x≤-3 -4 -15
-3≤x≤-1 -2 3
-1≤x≤1 0 -3
x≥1 2 15

8. Rough Sketching

9. Points to follow
For positive odd degree polynomial functions:
The graph will be rising from the left and rising to the
right.

10. Graph : f(x)= (𝑥 + 1) (𝑥 − 2) (𝑥 − 4)
Rising to
the right
Rising from
the left

11. Points to follow
For negative odd degree polynomial function:
The graph will be falling from the left and falling to the
right.

12. Graph : f(x)= -(𝑥 + 3) (𝑥 + 2) (𝑥 − 1)3
Falling from the left
Falling to the right

13. Points to follow
For positive even degree polynomial functions:
The graph will be falling from the left and rising to the
right.

14. Graph : y= 𝑥4
-2𝑥2
-15
Falling from the left Rising to the right

15. Points to follow
For negative even degree polynomial functions:
The graph will be rising from the left and falling to the
right.

16. Graph: f(x)= -x 𝑥 + 5 2
(𝑥 + 3)
Rising
from the
left
Falling to
the right

17. Points to follow
The characteristic of multiplicity ( odd or even ) will
determine the behavior of the graph relative to x-axis
at the given root.
If the characteristic of multiplicity is odd, it will cross
the x-axis.
If the characteristic of multiplicity is even, it will bounce
at the x-axis.

18. Root or Zero Multiplicity Characteristic
of Multiplicity
Behavior of
graph relative
to x-axis at this
root
-2 2 Even Bounces
-1 3 Odd Crosses
1 4 Even Bounces
2 1 Odd Crosses

19. Example: y= (𝑥 + 2)2(𝑥 + 1)3(𝑥 − 1)4 (𝑥 − 2)