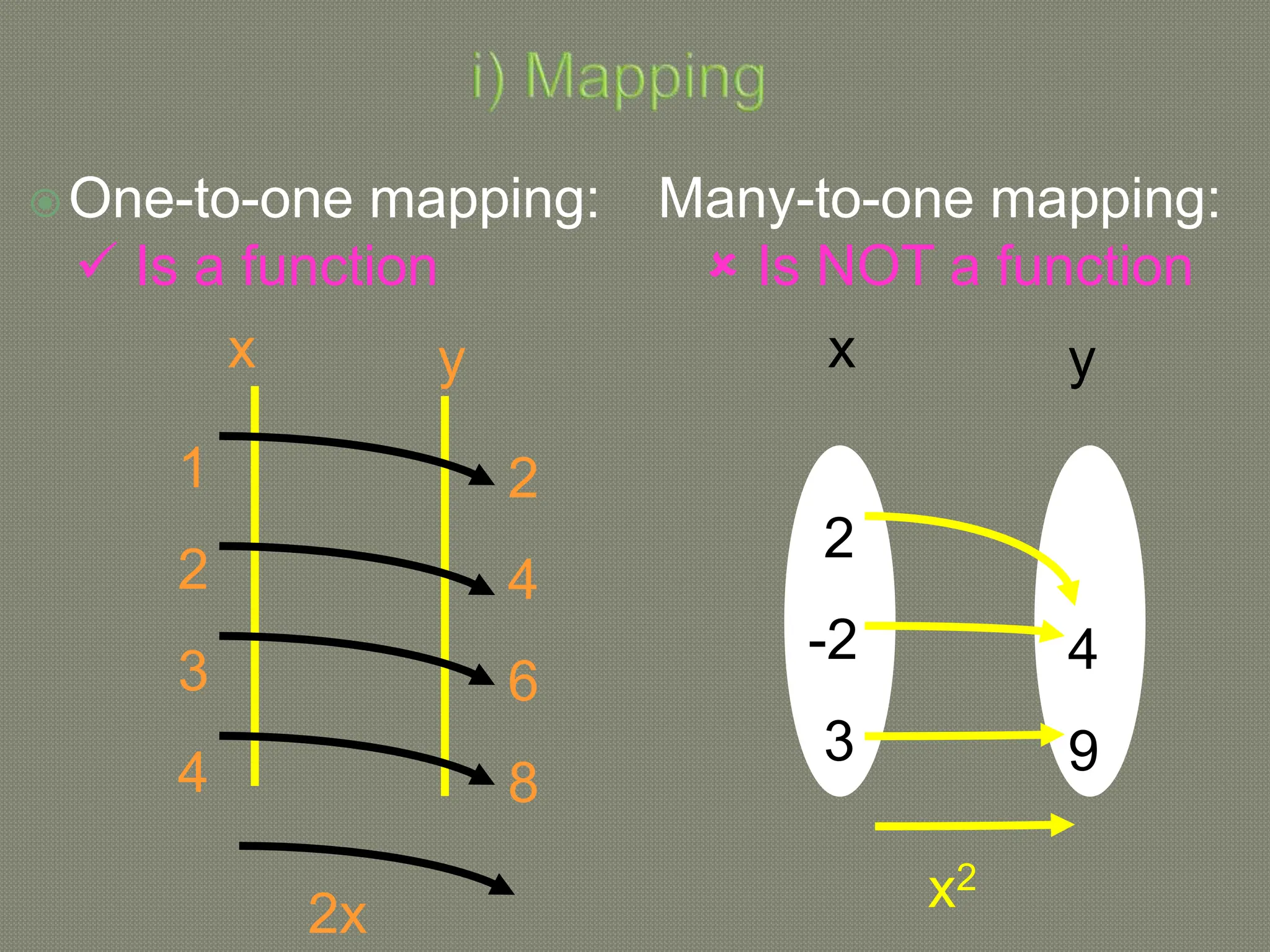
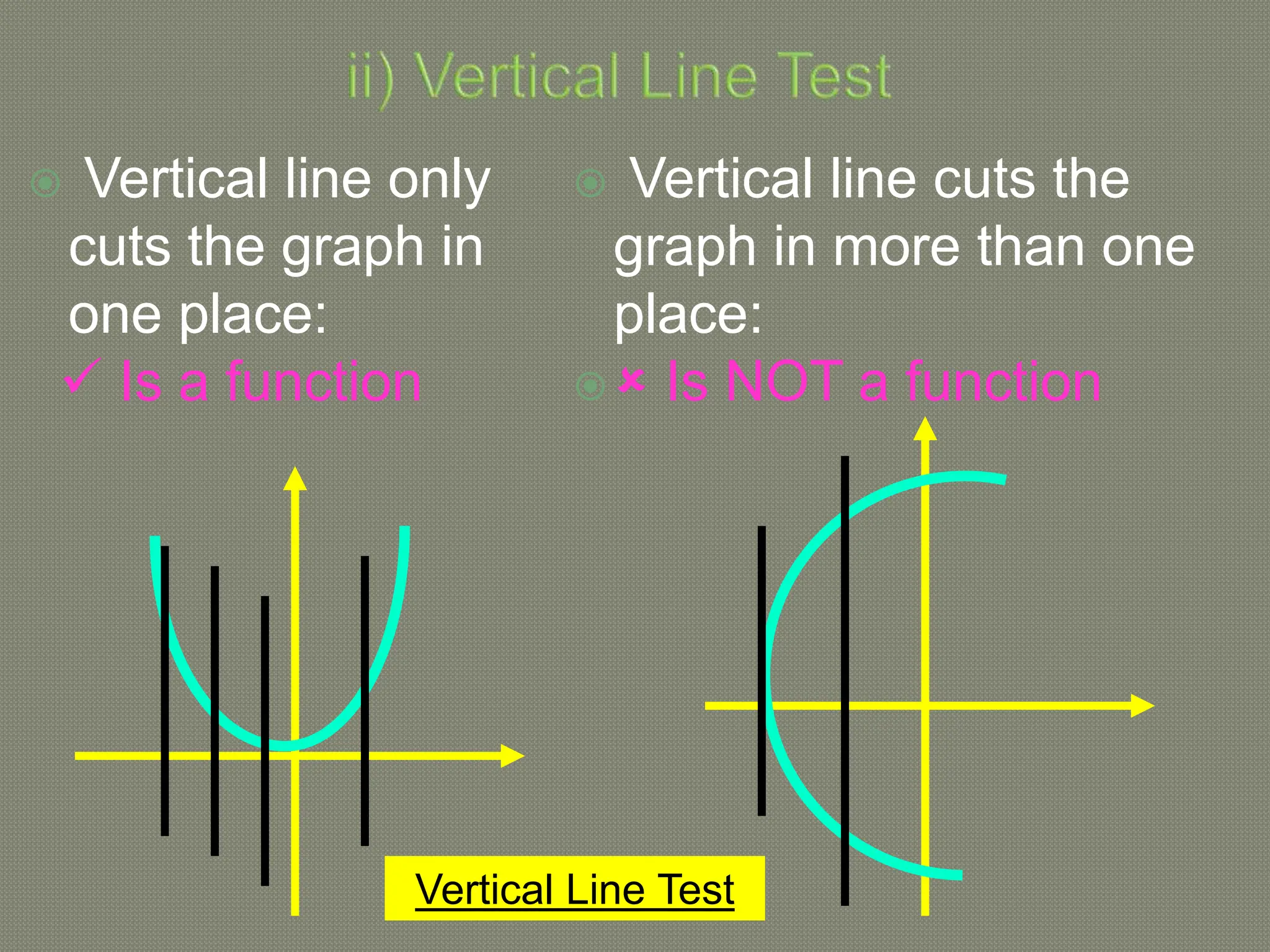
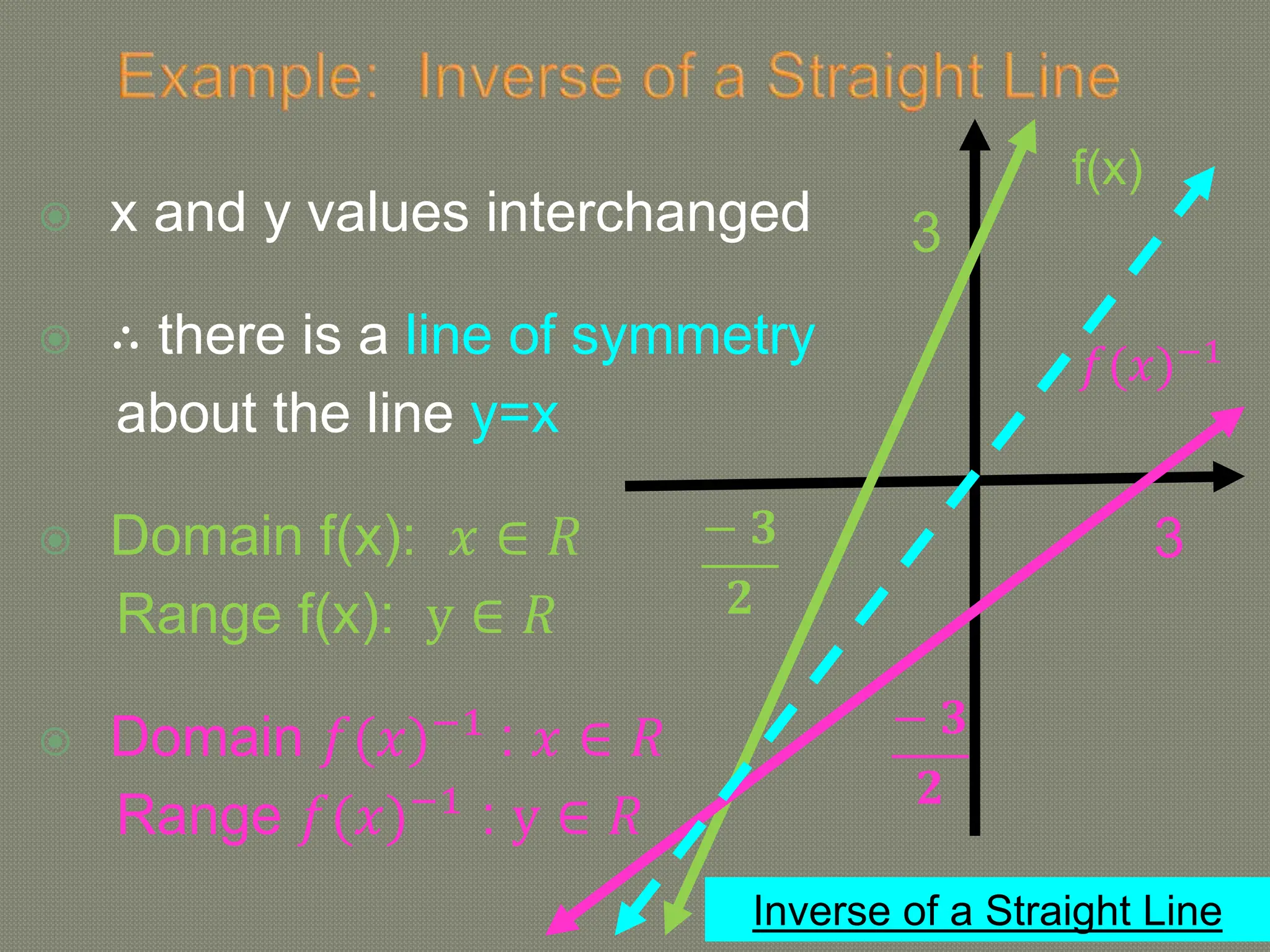
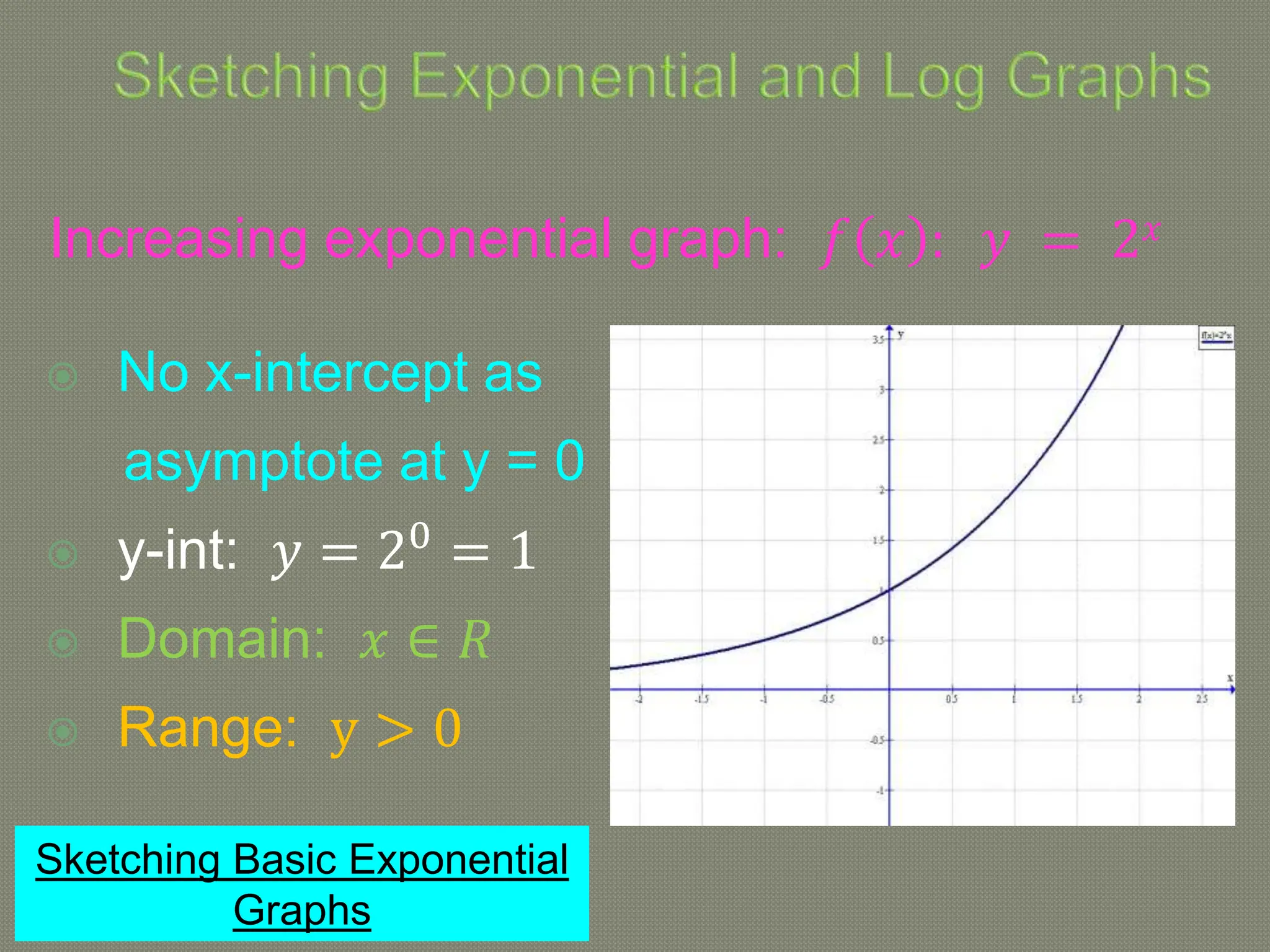
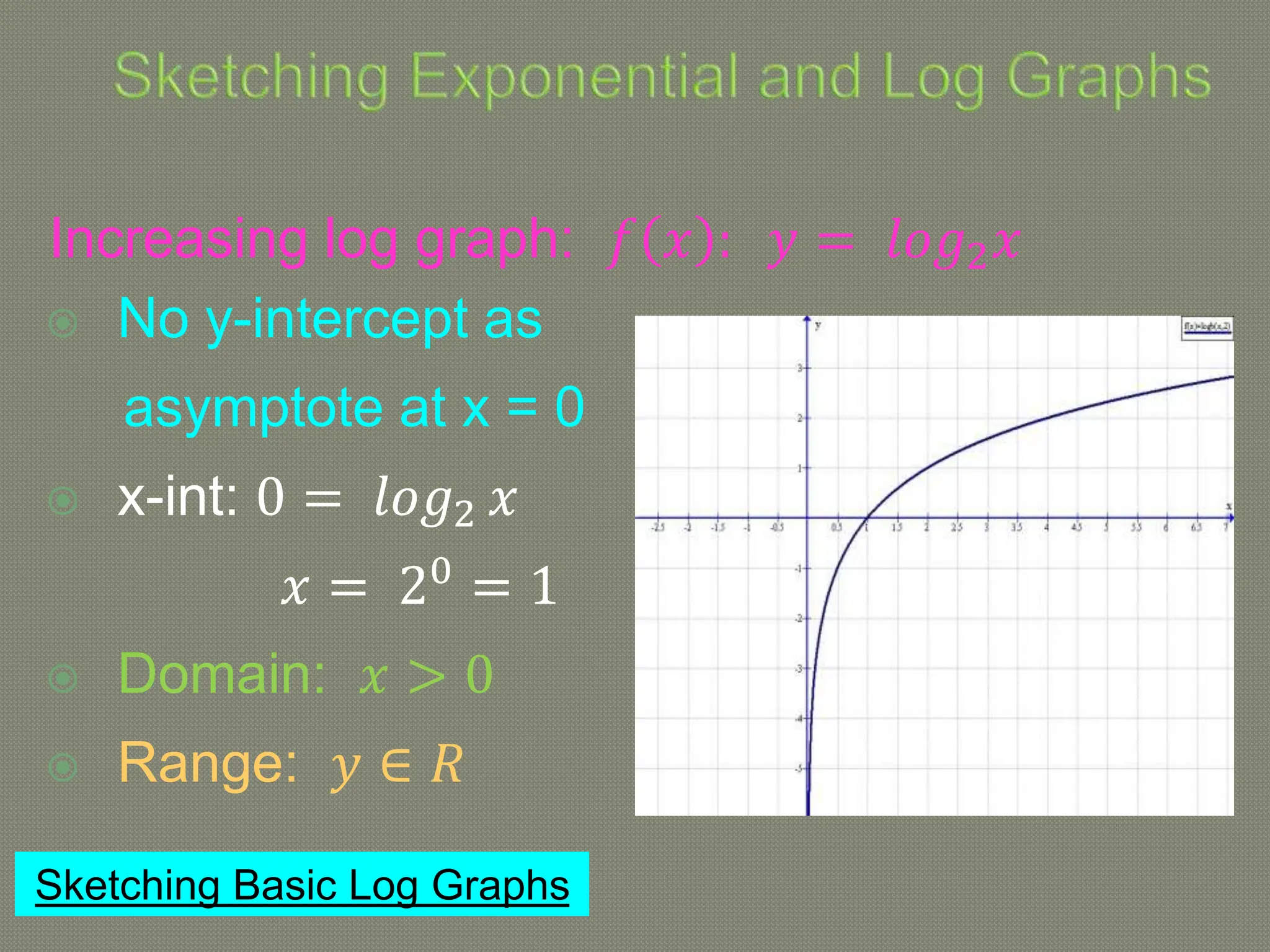
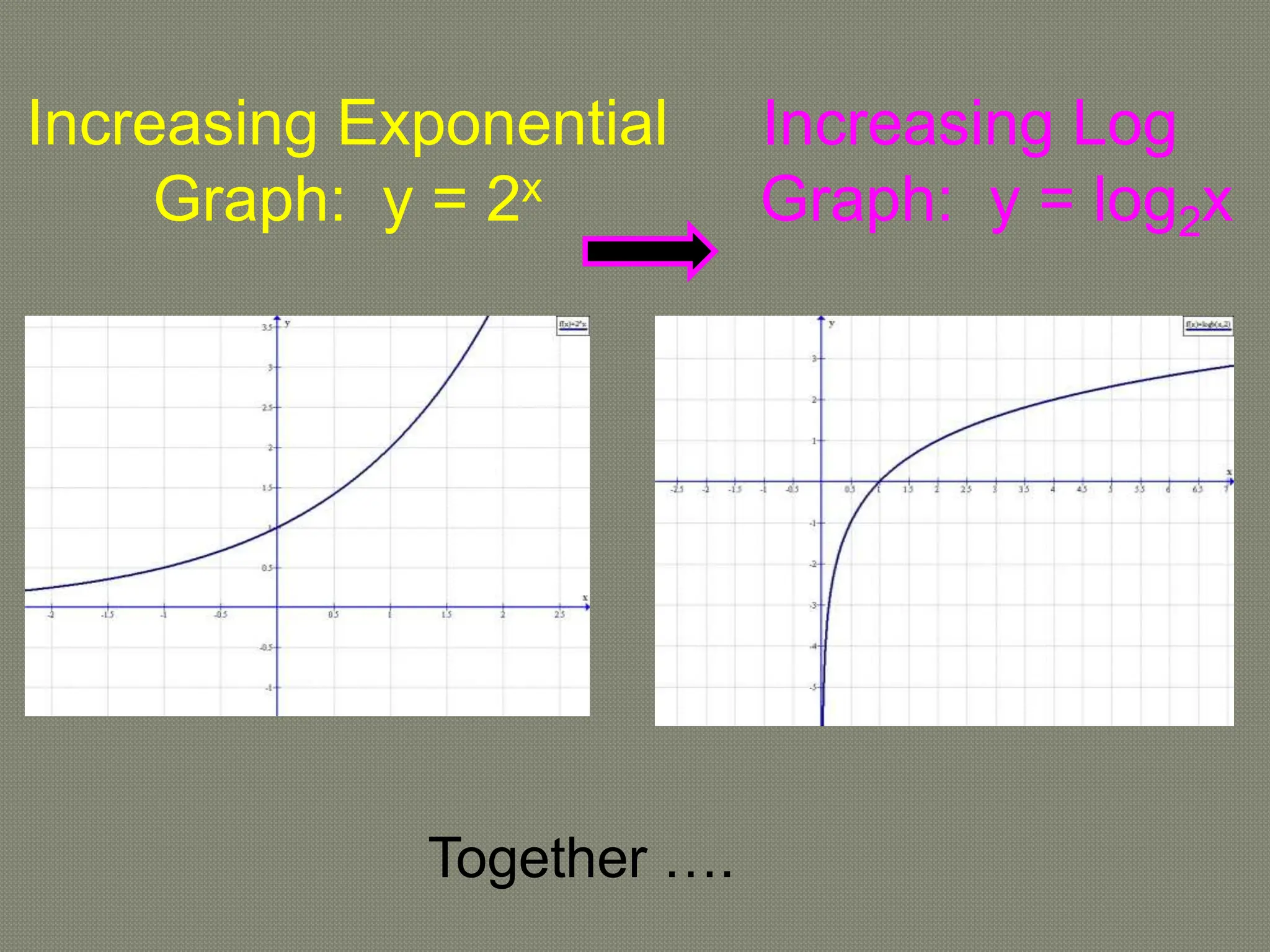
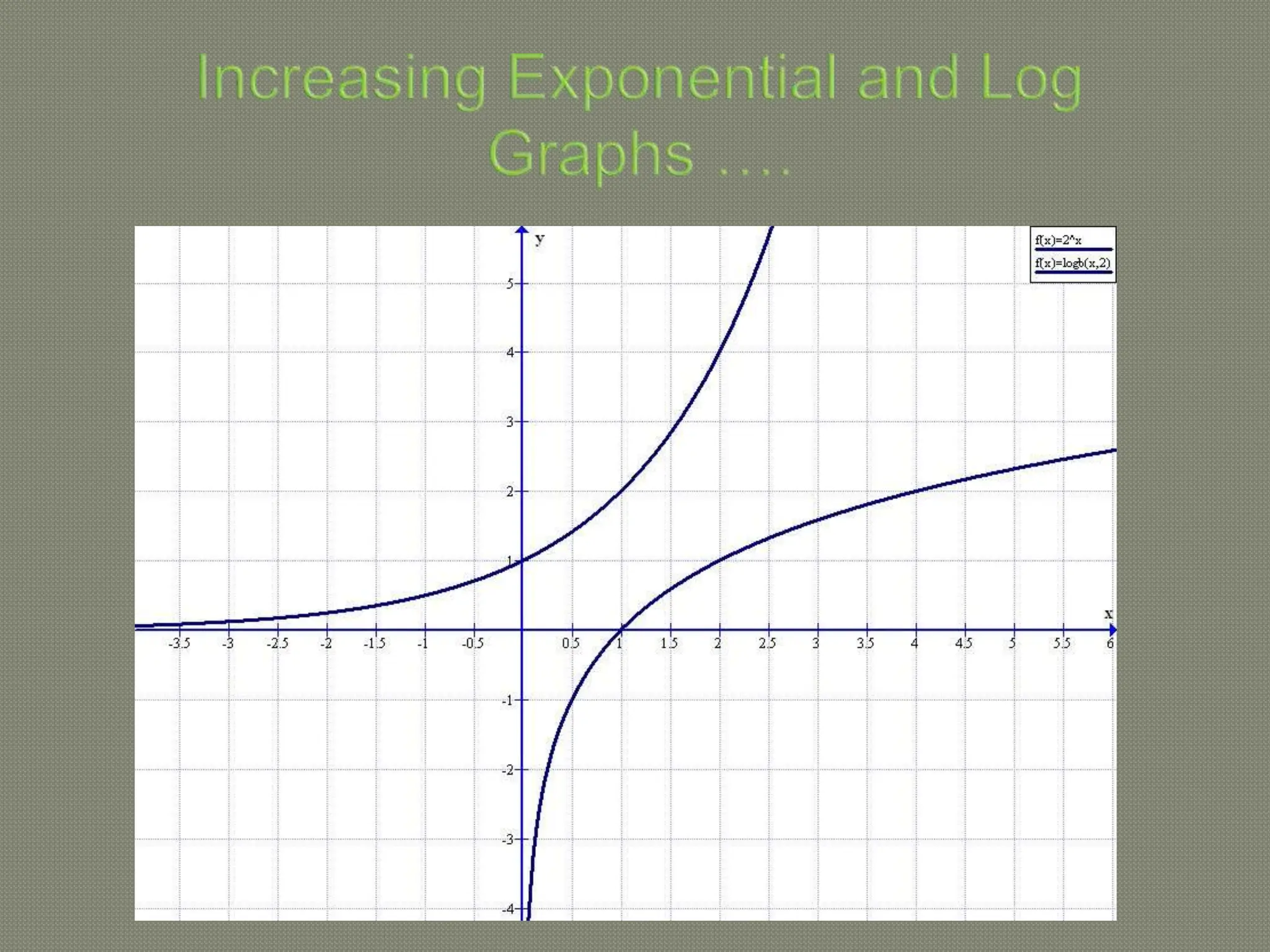
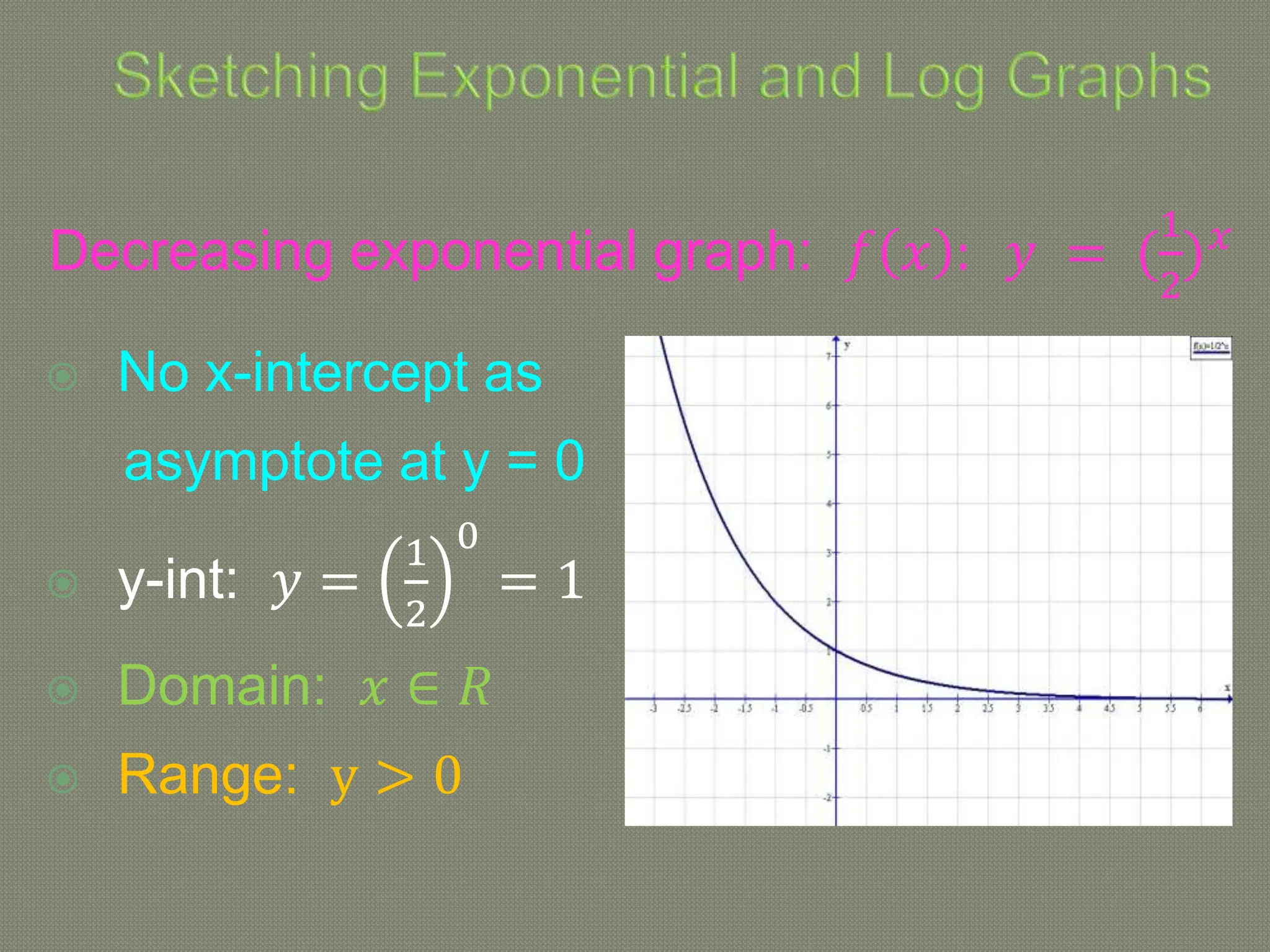
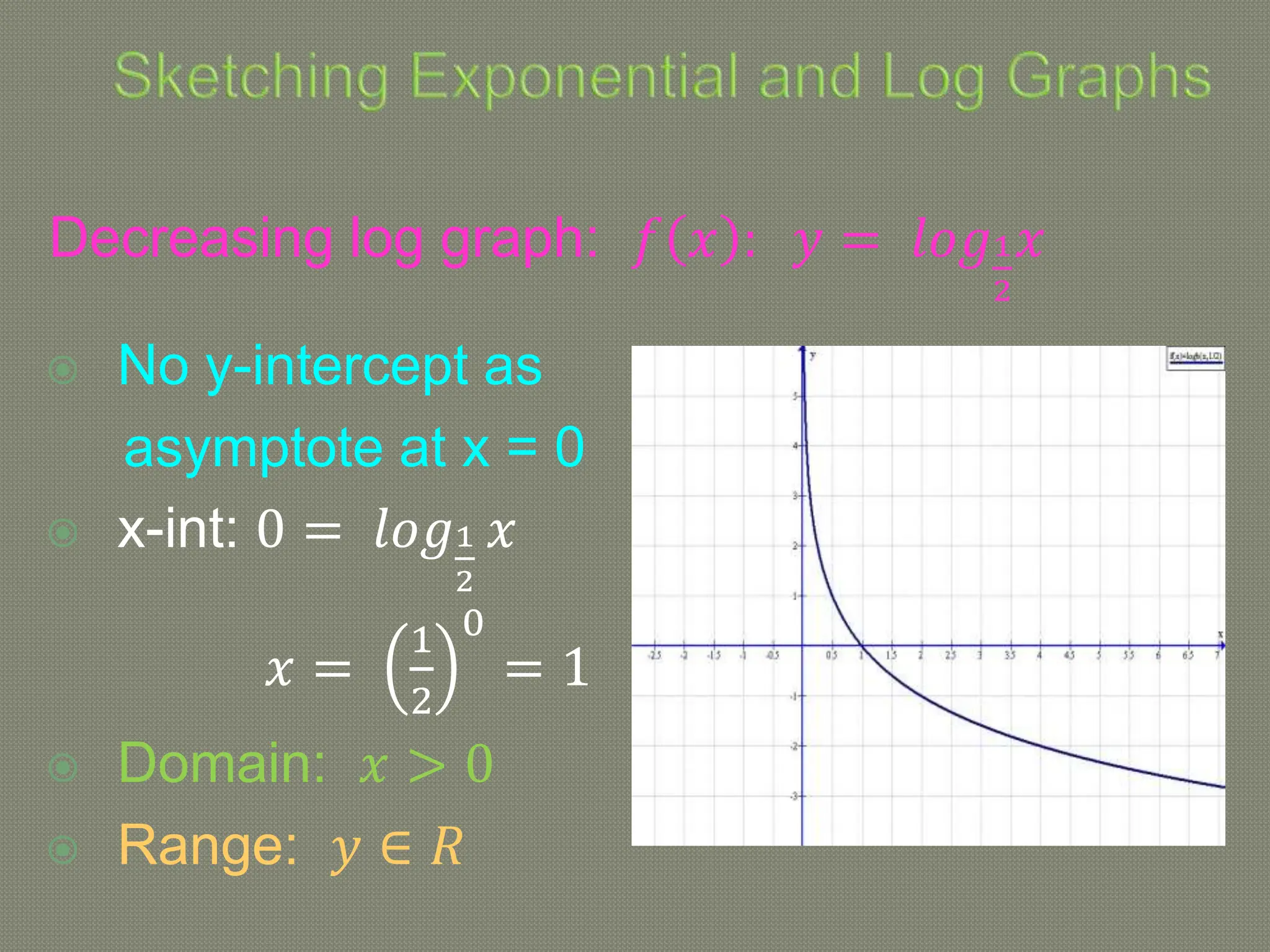
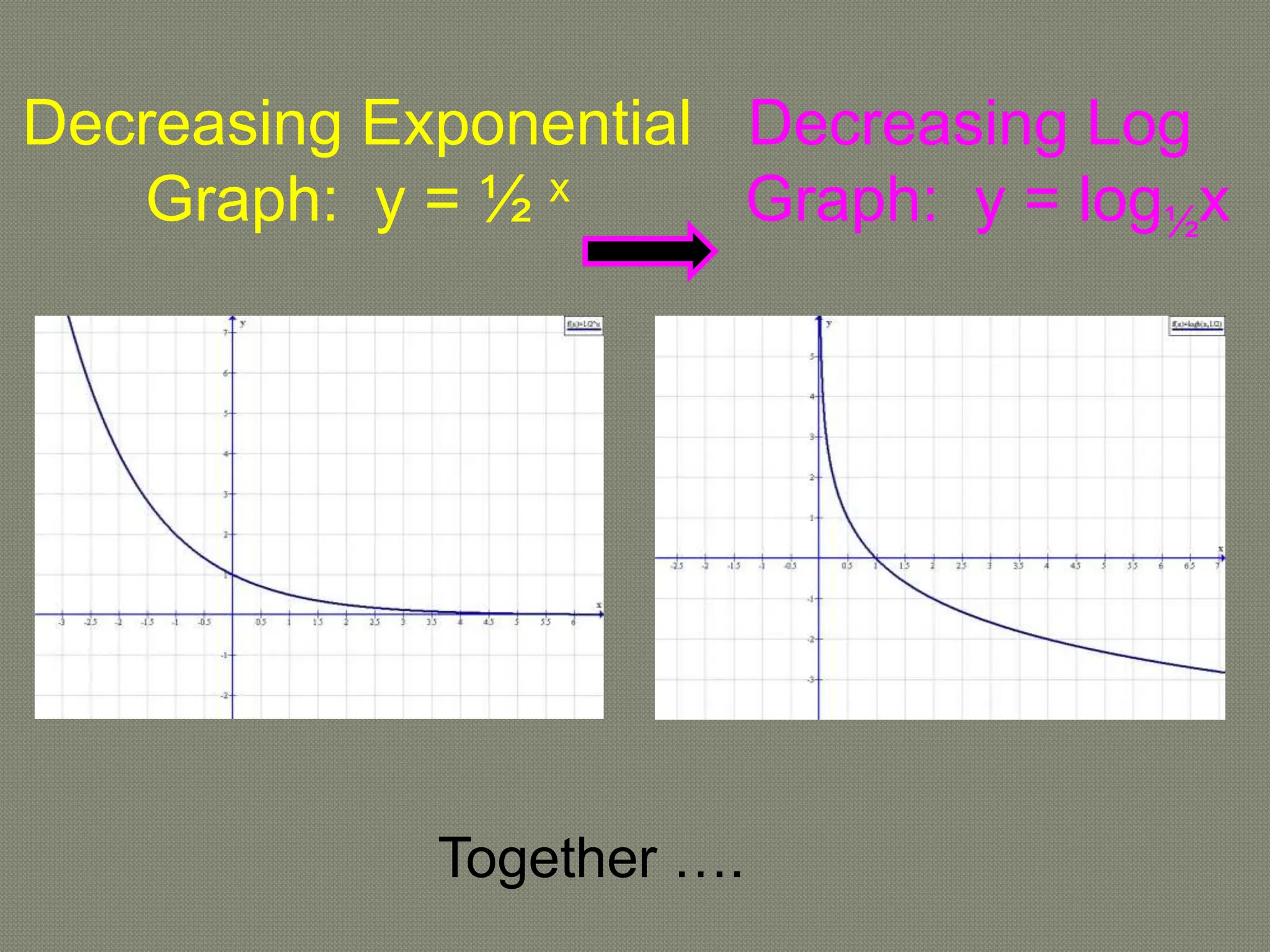
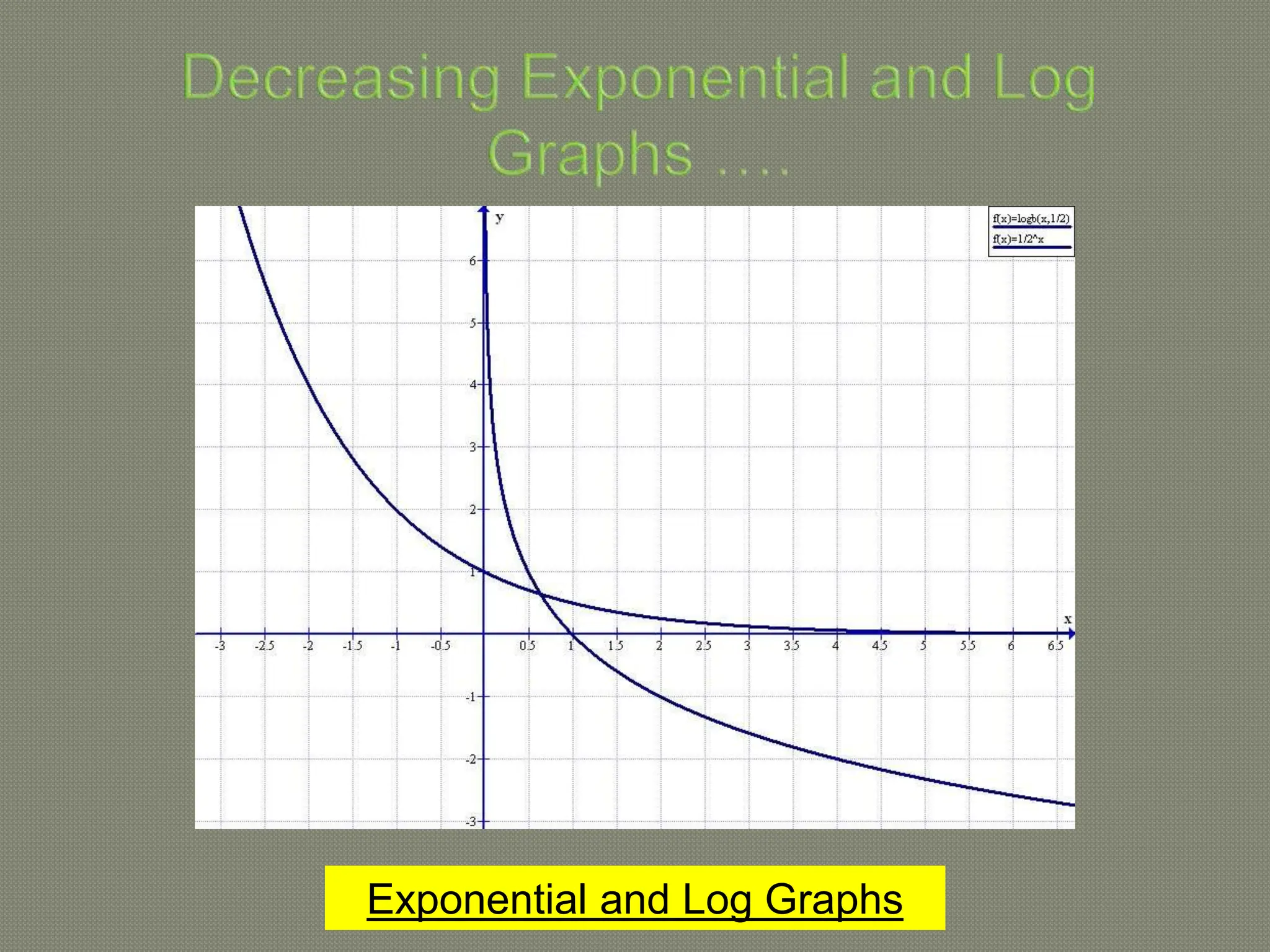
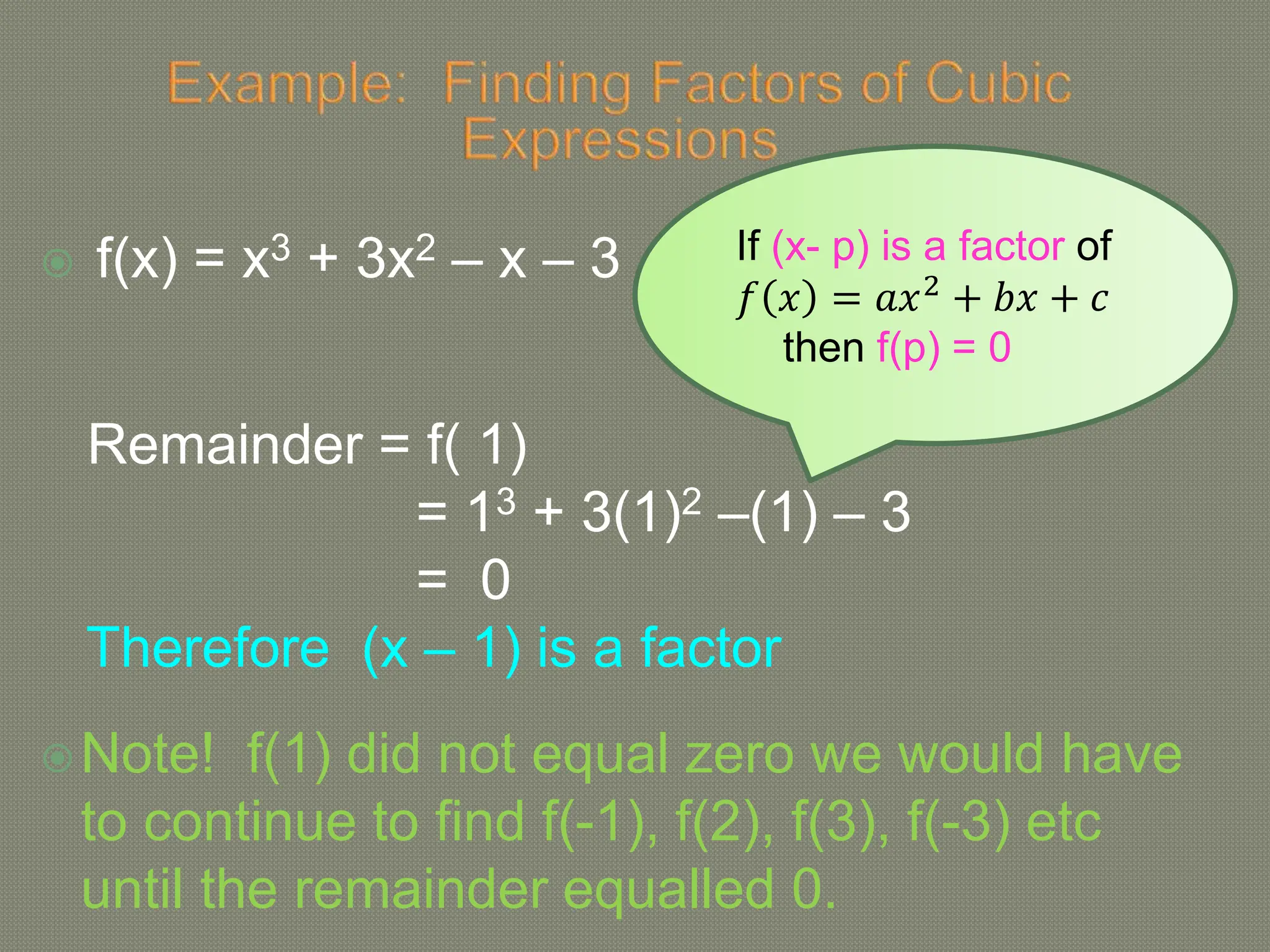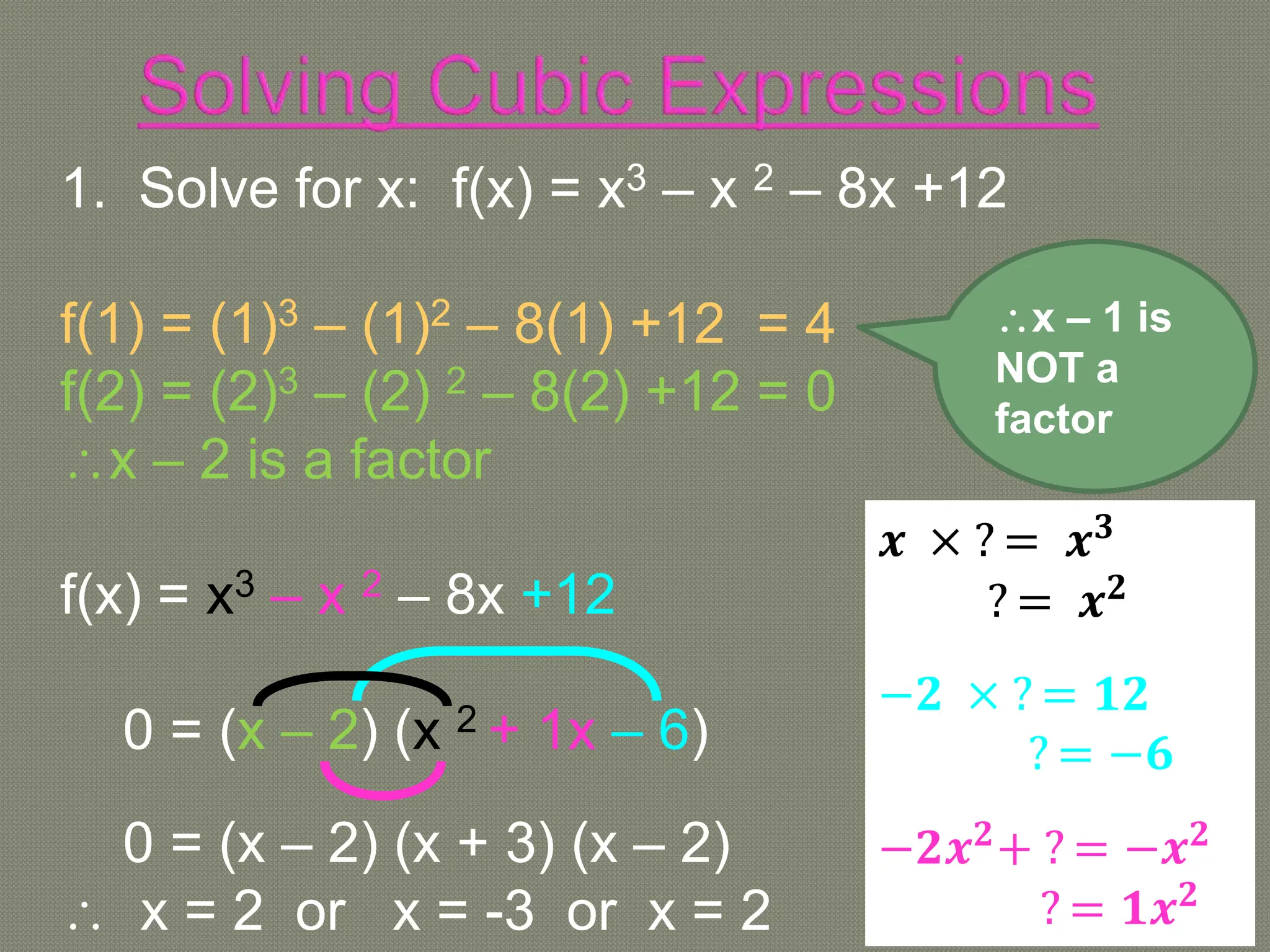The document discusses functions and their inverses. It defines key terms like domain, range, and inverse functions. It provides examples of determining if a relationship is a function using the vertical line test or one-to-one mapping. The document also covers finding inverses of straight lines, parabolas, exponential graphs and logarithmic graphs. It shows how to sketch these graphs and determine their domains and ranges. Finally, it discusses solving cubic expressions through finding factors and remainders.