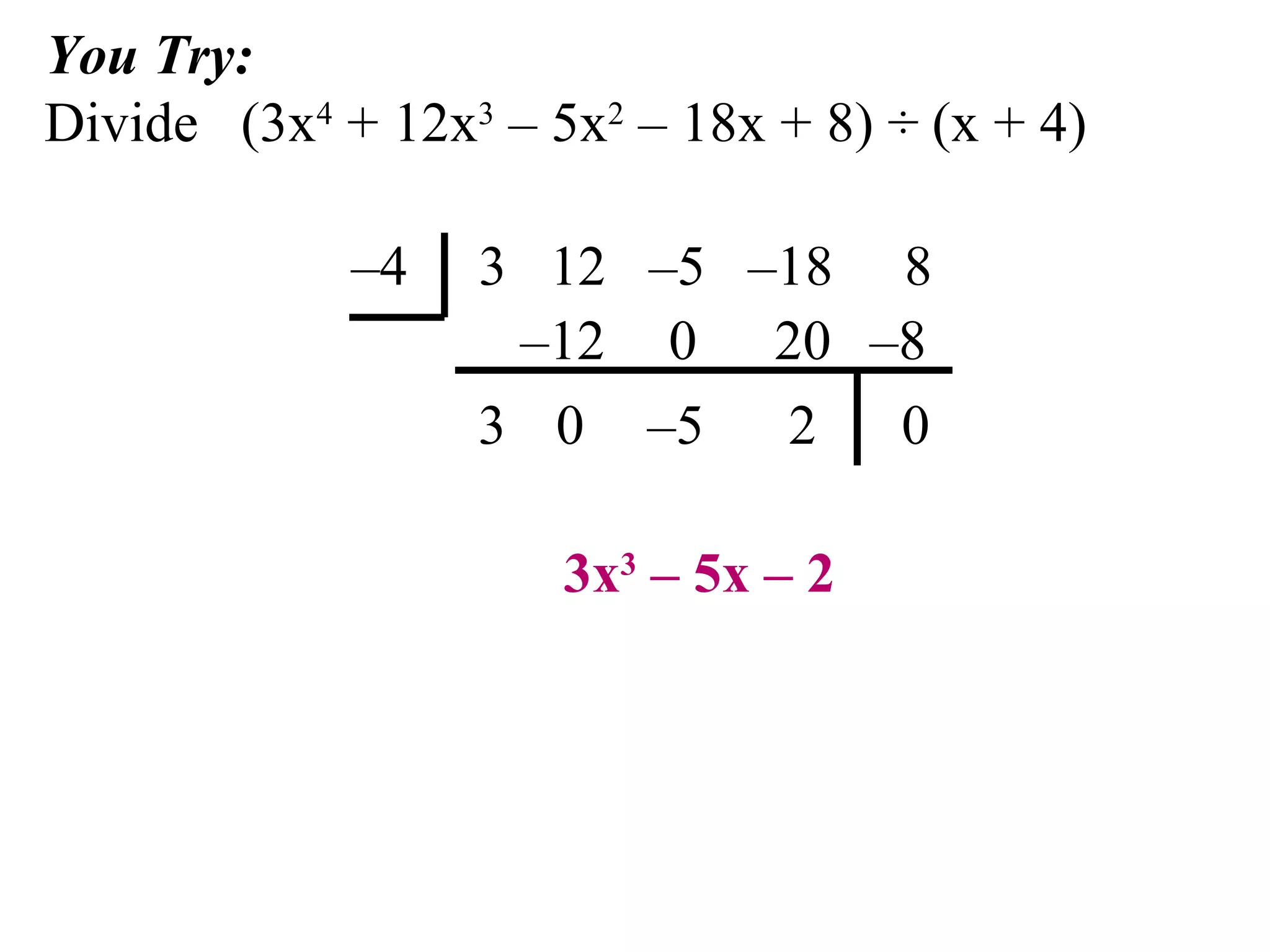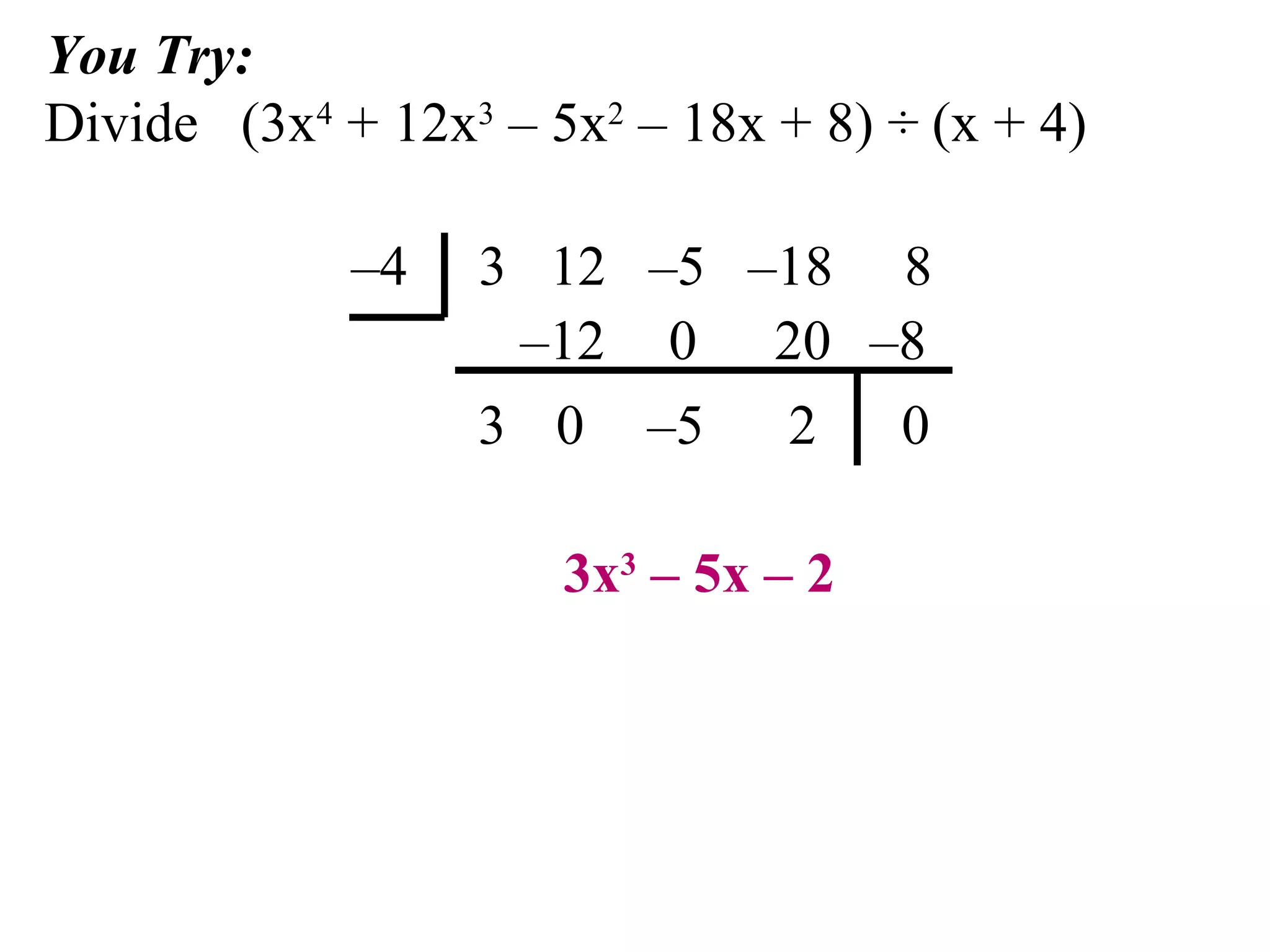
The document provides an explanation and examples of using synthetic division to divide polynomials. Synthetic division allows dividing a polynomial by a divisor of the form (x - k). The process involves writing the coefficients of the dividend in descending order and placing k below. Then, successive multiplication and addition steps provide the coefficients of the quotient polynomial and remainder. Two examples are worked through to demonstrate synthetic division for (2x^3 - 7x^2 - 8x + 16) / (x - 4) and (5x^3 + x^2 - 7) / (x + 1).

1. Warm up Divide

2. Synthetic division can be used when the divisor is in the form (x – k). Example: Use synthetic division for the following (2x 3 – 7x 2 – 8x + 16) ÷ (x – 4) First, write down the coefficients in descending order, and k of the divisor in the form x – k : 4 2 –7 –8 16 k 2 Bring down the first coefficient. 8 Multiply this by k 1 Add the column. 4 – 4 – 16 0 These are the coefficients of the quotient (and the remainder) 2x 2 + x – 4 Repeat the process.

3. Example: Divide (5x 3 + x 2 – 7) ÷ (x + 1) –1 5 1 0 –7 Notice that k is –1 since synthetic division works for divisors in the form (x – k). place-holder 5x 2 – 4x + 4 – 11 x + 1 5 – 5 – 4 4 4 – 4 – 11

4. You Try: Divide (3x 4 + 12x 3 – 5x 2 – 18x + 8) ÷ (x + 4) –4 3 12 –5 –18 8 3x 3 – 5x – 2 3 – 12 0 0 – 5 20 2 – 8 0