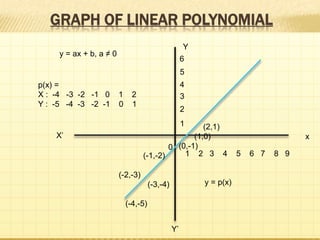
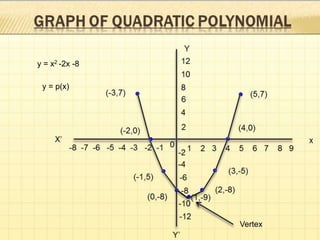
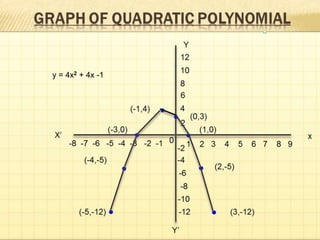
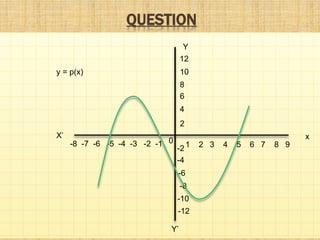
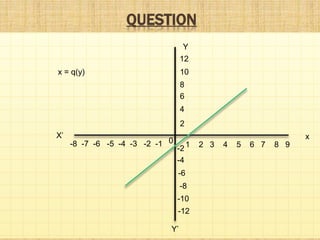
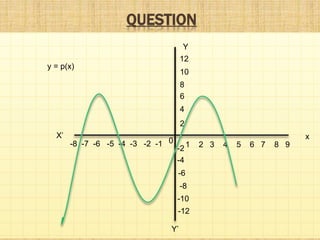
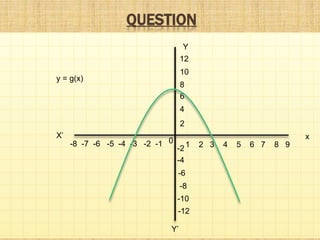
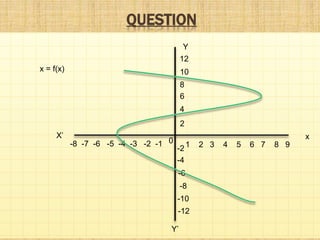
This document provides information about polynomials including definitions, types, terms, and relationships between coefficients and zeros. It begins with acknowledging those who helped create the presentation. It then defines a polynomial as an expression with variable terms raised to whole number powers. The main types discussed are linear, quadratic, and cubic polynomials. Linear polynomials have one zero while quadratics have two zeros and cubics have three. Relationships are defined between the zeros and coefficients. Graphs of linear and quadratic polynomials are presented. The division algorithm for polynomials is also explained.

3. ACKNOWLEDGEMENT
To our readers whom we owe all our hard work
and dedication. The main motive behind this
presentation is to convey some facts and data
related to polynomials.
Special thanks :-
To our parents who provided all the materials
and their valuable advice which helped me to
make the presentation more attractive.

4. ×Acknowledgement
To my friends and teachers who gave their
helping hand in the completion of this project
work.
To our elder brothers and sisters for their
support .

5. PREFACE
 In this context, we are going to discuss about some of
the terms and facts related to polynomial.
 Further we will discuss about the different types of
polynomials.
 We will learn about the quadratic polynomials in detail.
 We will also come across the relationship between the
zeroes of a polynomial to its coefficients.
 We shall also get a short recap of the remainder and
factor theorem.
 We shall also revise the different algebraic identities.

6. POLYNOMIALS
 A polynomial {i.e., p(x)} is an algebraic expression
consisting of constants and variables where the
exponential power of the variable is a whole
number.
 The general form of polynomial is-
p(x)= anxn + an-1xn-1 + ….. + a2x2 + a1x + a0 ,
where a0, a1 , a2 , a3 , …, an are the coefficients of
x0 , x1 , x2 ,…, xn and an ≠ 0.

7. TYPES OF POLYNOMIALS
 Polynomials are of various types depending upon:-
 Degree of a polynomial
 Linear
e.g. :- 2x + y
 Quadratic
e.g. :- 4x2- 2y +7
 Cubic
e.g. :- ax3 – 3b + 6
 Biquadratic
e.g. :- -5x4 + 6x3 + 7x2 + 3x + 6

8.  Types of polynomial
 Number of terms in a polynomial
 Monomial
e.g. :-
 Binomial
e.g. :-
 Trinomial
e.g. :-
 Polynomial
e.g. :- types of polynomial

9. Question
O Why does a polynomial of degree one is
called a linear polynomial?
Ans. A polynomial of degree one is called a
linear polynomial because it forms a straight
line by joining the points on the graph or
Cartesian plane.

10. Question
O Differentiate the types of polynomials
listed below?
y2 + 21/2 – quadratic, binomial
3t1/2 + t21/2 - not a polynomial
2x2 + 71/3 + x3 – cubic, trinomial
2 – x2 +x4 – biquadratic, trinomial
3y2 – 3x + 111/2 – quadratic, trinomial

11. TERMS AND TERMINOLOGY
Coefficient – it refers to the constant in each term of a
polynomial. Each term has a coefficient.
Constant polynomial – a polynomial consisting of
constants only, where the value of variable is 1 and degree
is 0, is called a constant polynomial.
e.g. :- 6 = 6x0 = 6 (1) = 6
here, 6 is a constant polynomial.
Zero polynomial – the constant polynomial zero is called a
zero polynomial.
Degree :- the highest power of the variable is called the
degree of a polynomial.

12.  Terms and Terminology
Zeroes of a polynomial – it is the value of ‘x’ variable in
polynomial of one variable ‘x’ for which p(x) = 0.
A real number α is a zero of a polynomial p(x) only and
only if p(α) = 0.
 A zero of a polynomial need not to be zero.
 0 may or may not be the zero of a polynomial.
 Every linear polynomial has only and only one zero.
 A polynomial can have more than one zero.
 The zeroes of a polynomial depends upon the degree
of the polynomial.

13. Question
O What is the degree of the polynomial
listed below?
Non-zero constant polynomial :– 0
Zero constant polynomial :– not defined
-7y5 + 3 :– 5
5 t – y2 :– 2
π + 5x :- 1

14. Question
O Find the coefficient of x2 :–
2 - x2 + 7 :- -1
4x +7 x2 – 2 :- 7

15. Question
O Find whether the following are zeroes of
p(x) or not :-
Ans. (x+1)(x-2), x= -1,2
p(x) = (x+1)(x-2)
p(-1) = (-1 +1) (-1 -2)
= (0) (-3) = 0
p(2) = (2+1) ( 2-2)
= (3) (0) = 0

16. Question
O Find the zeroes of the polynomial?
p(x) = cx + d , c ≠ 0
p(x) = 2x +5
p(x) = (x + 1) (x – 2)

17. LINEAR POLYNOMIAL
 A linear polynomial is generally of the form:-
p(x) = ax + b, a ≠ 0
As we know that a linear polynomial has only one zero of
a polynomial.
Let p(α) = 0;
α = - b/a = - (constant term/ coefficient of x)
 The graph of a linear equation is a straight line. So,
For, y = p(x)
The graph line will pass through the ‘X’ axis for once only.
Thus, indicating that it has only one zero of a polynomial,
namely, ( -b/a , 0).

18. GRAPH OF LINEAR POLYNOMIAL
Y
Y’
xX’
0
y = p(x)
y = ax + b, a ≠ 0
p(x) =
X : -4 -3 -2 -1 0 1 2
Y : -5 -4 -3 -2 -1 0 1
1 2 3 4 5 6 7 8 9
6
5
4
3
2
1 (2,1)
(1,0)
(0,-1)
(-1,-2)
(-2,-3)
(-3,-4)
(-4,-5)

19. QUADRATIC POLYNOMIAL
 A quadratic polynomial is generally of the form:-
p(x) = ax2 + bx + c, a ≠ 0
As we know that a quadratic polynomial has only
two zeroes of a polynomial.
Let p(α) = 0 and p(β) = 0;
α + β = - b/a = - (coefficient of x/ coefficient of x2)
α β = c/a = (constant term/ coefficient of x2)
 The graph of a quadratic equation is a curved line
called is parabola. So,
For, y = p(x)
The graph line will pass through the ‘X’ axis for
once only. Thus, indicating that it has only one zero
of a polynomial, namely, ( -b/a , 0).

20.  Quadratic Polynomial
 A parabola is a curved line obtained by joining the
points on the graph of the polynomial
f(x) = ax2 + bx + c, where a ≠ 0.
 The lowest point P ,called minimum point , is the vertex
of the parabola.
 Vertical line passing through the point P is the axis of
parabola.
 The parabola is symmetrical about its axis, thus it is
also called line of symmetry.
 If the coefficient of x2 in f(x) = ax2 + bx + c, is a positive
real number then, parabola will open upwards,
otherwise if the coefficients of x2 is negative then it will
open downwards.

21. y = x2 -2x -8
y = p(x)
Vertex

22. GRAPH OF LINEAR POLYNOMIAL
Y
Y’
xX’
0 1 2 3 4 5 6 7 8 9
12
10
8
6
4
2
-8 -7 -6 -5 -4 -3 -2 -1
-2
-4
-6
-8
-10
-12 (3,-12)
(2,-5)
(1,0)
(0,3)
(-1,4)
(-3,0)
(-4,-5)
(-5,-12)
y = 4x2 + 4x -1

23. Question
O Find the degree of the polynomial and the
number of zeroes of the upcoming
polynomial ?

24. QUESTION
Y
Y’
xX’
0 1 2 3 4 5 6 7 8 9
12
10
8
6
4
2
-8 -7 -6 -5 -4 -3 -2 -1
-2
-4
-6
-8
-10
-12
y = p(x)

25. QUESTION
Y
Y’
xX’
0 1 2 3 4 5 6 7 8 9
12
10
8
6
4
2
-8 -7 -6 -5 -4 -3 -2 -1
-2
-4
-6
-8
-10
-12
x = q(y)

26. QUESTION
Y
Y’
xX’
0 1 2 3 4 5 6 7 8 9
12
10
8
6
4
2
-8 -7 -6 -5 -4 -3 -2 -1
-2
-4
-6
-8
-10
-12
y = p(x)

27. QUESTION
Y
Y’
xX’
0 1 2 3 4 5 6 7 8 9
12
10
8
6
4
2
-8 -7 -6 -5 -4 -3 -2 -1
-2
-4
-6
-8
-10
-12
y = g(x)

28. QUESTION
Y
Y’
xX’
0 1 2 3 4 5 6 7 8 9
12
10
8
6
4
2
-8 -7 -6 -5 -4 -3 -2 -1
-2
-4
-6
-8
-10
-12
x = f(x)

29. RELATION OF ZEROES AND COEFFICIENTS OF LINEAR
AND QUADRATIC POLYNOMIAL
 In linear polynomial,
p(α) = ax + b
α = -b/a = - (constant term/coefficient of x)
 In quadratic polynomial,
p(x) = ax2 + bx + c, a ≠ 0
p(α) = 0 and p(β) = 0
α + β = -b/a = - ( coefficient of x/ coefficient of x2)
αβ = c/a = (constant term/ coefficient of x2)

30. Question
O Find the zeroes of the polynomial and
verify the relationship?
Ans. p(x) = x2 + 7x + 12
x2 + 4x + 3x +12
x(x + 4) + 3(x + 4)
(x + 4) (x + 3)
so, x = -4, -3
(P.T.O.)

31.  question
Now we have to verify the relationship;
α = -3 ; β = -4
a = 1 ; b = 7 ; c = 12.
α + β = (-3 -4) = -7 = -7/1
= -(coefficient of x /coefficient of x2)
αβ = (-3 × -4) = 12 = 12/1
= (constant term / coefficient of x2)

32. Question
O Find the zeroes of the following
polynomial and verify the relationship?
1. f(u) = 4u2 + 8u
2. p(x) = abx2 + (b2 – ac) x – bc
3. p(x) = x2 + (1/6)x – 2
4. p(x) = x2 – 5x + k , such that α – β = 1
find k then proceed.
5. f(x) = 2x2 + 5x + k, such that α2 + β2 +2αβ
,find the value of k then proceed further.

33. Question
O If α + β = 24 and α – β = 8, then find the
polynomial having α , β as its zeroes.
O If α , β are the zeroes of quadratic
polynomial then evaluate:-
1. α – β
2. α4 + β4
3. α2 + β2
4. (1/α) + (1/β) – 2αβ

34. RELATIONSHIP OF ZEROES AND COEFFICIENTS
OF CUBIC POLYNOMIAL
 In cubic polynomial,
p(x) = ax3 + bx2 + cx + d, a ≠ 0
p(α) = 0 , p(β) = 0, p(γ) = 0
α + β + γ = -b/a = -(coefficient of x2/ coefficient of x3)
αβ + βγ + γα =(c/a) =(coefficient of x/ coefficient of x3)
αβγ = -d/a = -(constant term/ coefficient of x3)

35. Question
O Verify 3,-1, -(1/3) are zeroes of p(x)=3x3 -
5x2 - 11x – 3 and also the relationship of
zeroes and coefficients?
O Find a cubic polynomial with sum, sum of
product of zeroes taken two at a time, and
product of zeroes as 2, -7, -14
respectively?
O p(x) = x3 - 6x2 + 3x + 10 have zeroes a,
a + b, a + 2b, find the value of a and b
also its zeroes?

36. Question
O If the zeroes of f(x) = ax3 + 3bx2 + 3cx + d
are in arithmetic progression ., then prove
that 2b3 – 3abc + a2d = 0?
O Find the zeroes of the polynomial f(x) = x2
– 12 x2 + 39x – 28, and the zeroes are in
arithmetic progression?

37. DIVISION ALGORITHM FOR POLYNOMIAL
 We have seen that on division of an integer by a non-
zero integer, we obtain the quotient and the remainder
which is either zero or less than the divisor.
 Dividend = divisor × quotient + remainder
This is also know as Euclid’s Division Lemma.
,i.e., a = bq + r
This can be re-written as:-
p(x) = g(x) q(x) + r(x), where 0 > r(x) ≥ g(x)

38. Question
O Divide 2x2 + 3x + 1 by x + 2?
Ans. x + 2 2x2 + 3x + 1 2x – 1
2x2 + 4x
- -
- x + 1
- x - 2
+ +
3

39.  Question
Now, we have to verify that whether it
follows the division algorithm or not:-
,i.e., p(x) = g(x) q(x) + r(x)
L.H.S =
(x + 2) (2x – 1) + 3 = (x + 2) (2x – 1) + 3
= x(2x – 1) + 2(2x – 1)+3
= 2x2 – x + 4x – 2 + 3
= 2x2 + 3x – 2 + 3
= 2x2 + 3x + 1 = R.H.S
Hence, verified.

40. Question
O Divide p(x) = -1x3 + 3x2 - 3x + 5 by g(x)= x –
1 – x2 and verify the division algorithm?
O Find the other zeroes of polynomial:-
1. 2x4 – 3x3 – 3x2 + 6x – 2 ; 21/2 , -21/2
2. x4 – 6x3 – 26x2 + 138x – 35 ; 2 ± 31/2
O Find whether g(x) is factor of p(x) or not:-
1. p(x)=3x4 + 5x3 – 7x2 + 2x + 2 ; g(x)=x2 +3x
+1
2. p(x)= x3 – 3x2 + x + 2 ; g(x)= x2 - x +1

41. Question
O If p(x)= 6x4 + 8x3 + 17x2 + 21x + 7 is divided
by g(x)= 3x2 + 4x + 1, then r(x)= ax + b, find
a and b?
O If r(x)= 7 when p(x)= x3 + 2x2 + kx + 3 divided
by g(x)= x – 3 , find q(x) and k. also find the
zeroes of the polynomial?
O If x – 51/2 is a factor of p(x)= x3 – 3(5)1/2 x2 +
13x – 3(5)1/2, then find all the zeroes?

42. Question
O What must be added to p(x)= 4x4 + 2x3 – 2x2
+ x – 1, the polynomial is divisible by g(x)= x2
+ 2x – 3?
O When p(x)= ax3 + 3x2 – 13 and f(x)= 2x3 - 5x
+ a is divided by (x +2) and remainder is
same in both the case, then find the value of
‘a’?
O A quadratic polynomial in x leaves remainder
5 on dividing by (x-1) and 2 on dividing by
(x + 2). When p(x) is divided by (x-1)(x + 2),
then find the remainder?

43. Highest Common Factor and Lowest
Common Factor of Polynomials
 Factor of a polynomial:- if p(x) is a product of g(x) and
q(x), then g(x) and q(x) are its factors.
 H.C.F. :- The common factor of both the polynomial
which has the highest degree among all the factors is
called the highest common factor of the polynomial.
 L.C.M. :- The least common multiple of two or more
polynomials is the polynomial of the lowest degree
having smallest numerical coefficient which is exactly
divisible by the given polynomial of the given
polynomial and whose coefficient of highest degree
term has the same sign as the sign of the coefficient of
the highest degree term in the product.

44. RELATION BETWEEN L.C.M AND H.C.F
 LCM of {p(x) and f(x)} × HCF of {p(x) and f(x)}= p(x)
× f(x)
LCM × HCF = p(x) × f(x)
 This is applicable only for HCF and LCM of only two
polynomials.
for e.g.;
HCF{p(x),g(x),q(x)} × LCM{p(x),g(x),q(x)} =
{p(x),g(x),q(x)}

45. Question
O 150(6x2 + x – 1) ( x – 3)3 and 84(x – 3)2 (8x2
+ 14x + 5) ; find HCF?
Ans. Let f(x) = 150(6x2 + x – 1) ( x – 3)3
g(x) = 84(x – 3)2 (8x2 + 14x + 5)
Now,
f(x) = 150(6x2 + x – 1) ( x – 3)3
= 2 × 3 × 52 (2x + 1)(3x – 1)(x – 3)3
g(x) = 84(x – 3)2 (8x2 + 14x + 5)
= 22 × 3 × 7(x – 3)2 (2x + 1)(4x + 5)

46. Question
Hence, req. HCF = 2 × 3 (2x + 1) × (x – 3)2
= 6 (2x + 1)(x – 3)2
f(x) = 2 × 3 × 52 (2x + 1)(3x – 1)(x – 3)3
g(x)= 22 × 3 × 7(x – 3)2 (2x + 1)(4x + 5)
Hence,
req. LCM =22 × 3 × 52 × 7(x – 3)3(2x + 1)(3 – 1)
(4x + 5)

47. Question
O Find the LCM and HCF of the following:-
1. p(x) = (x – 3)(x2 + x – 2)
q(x) = x2 - 5x + 6
2. p(x) = 2(x4 – 1)
q(x) = (x+1) (x2 + 1)
O Find the HCF of x3 + 4x2 + x + 1 and x3 –
1. Hence find the value of ‘x’ for which
both the polynomial vanishes?

48. FACTOR THEOREM
 The factor theorem states that if a polynomial
p(x) and any real number a is divided x – a
then the rituraj