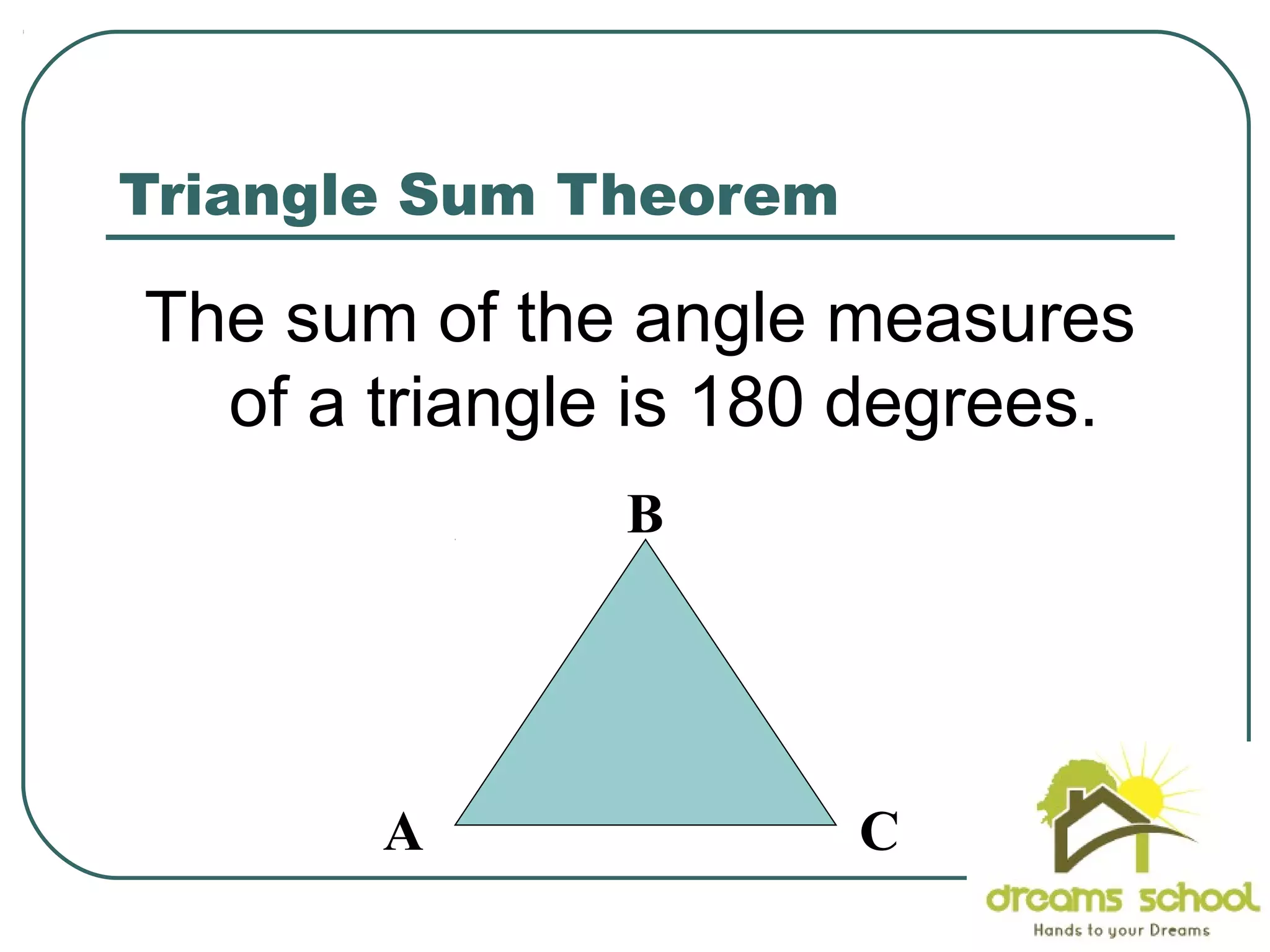
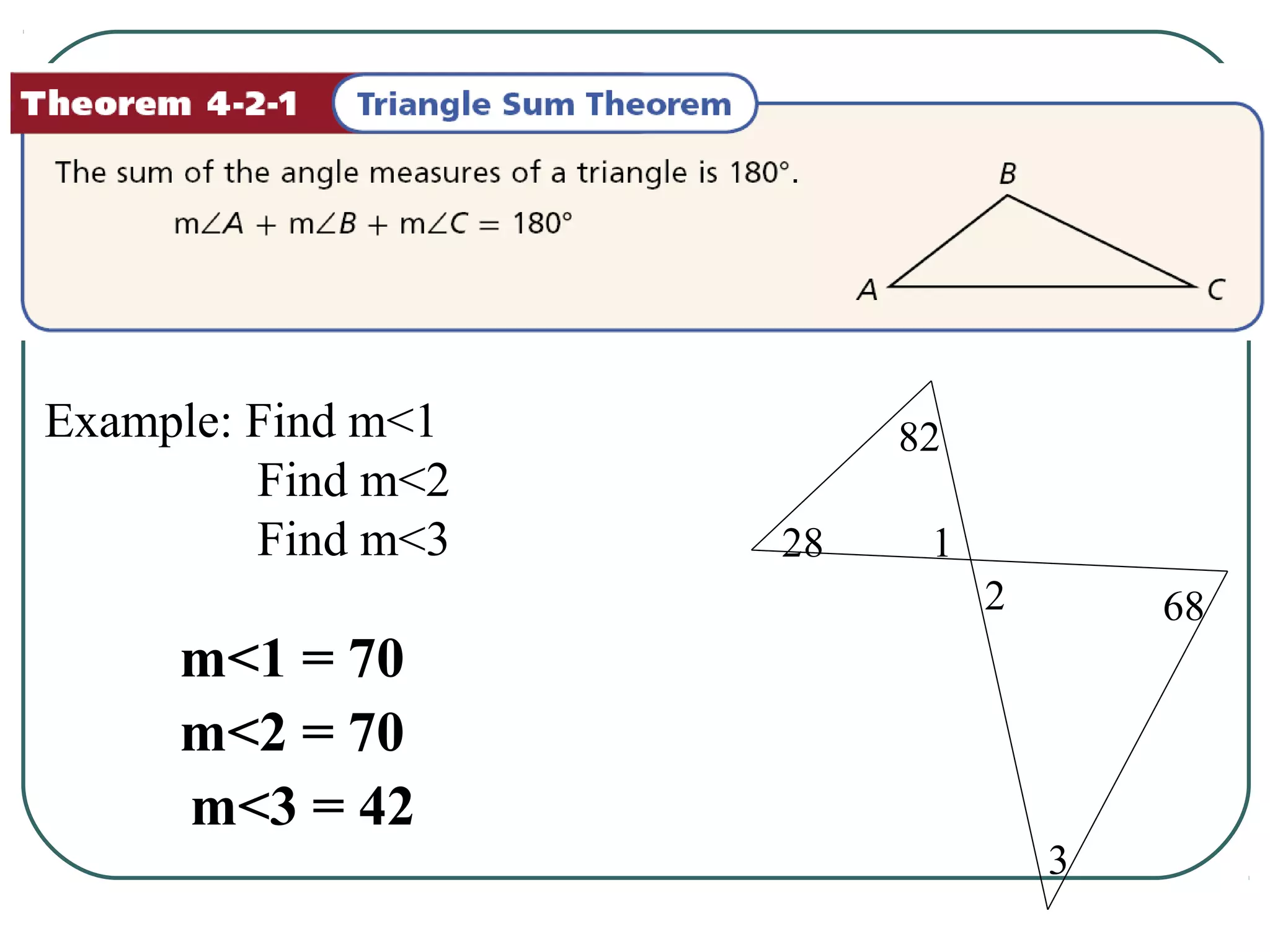
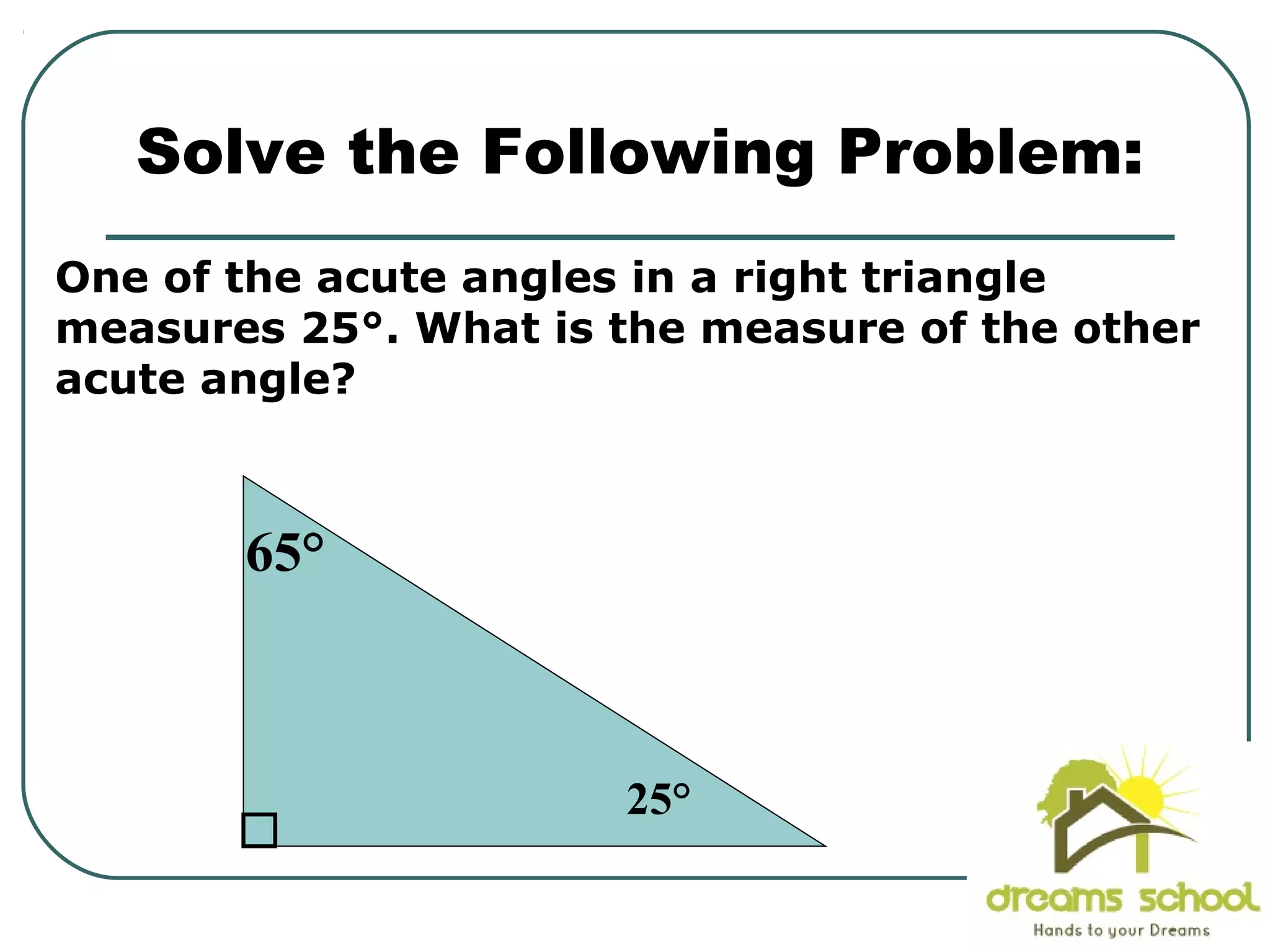
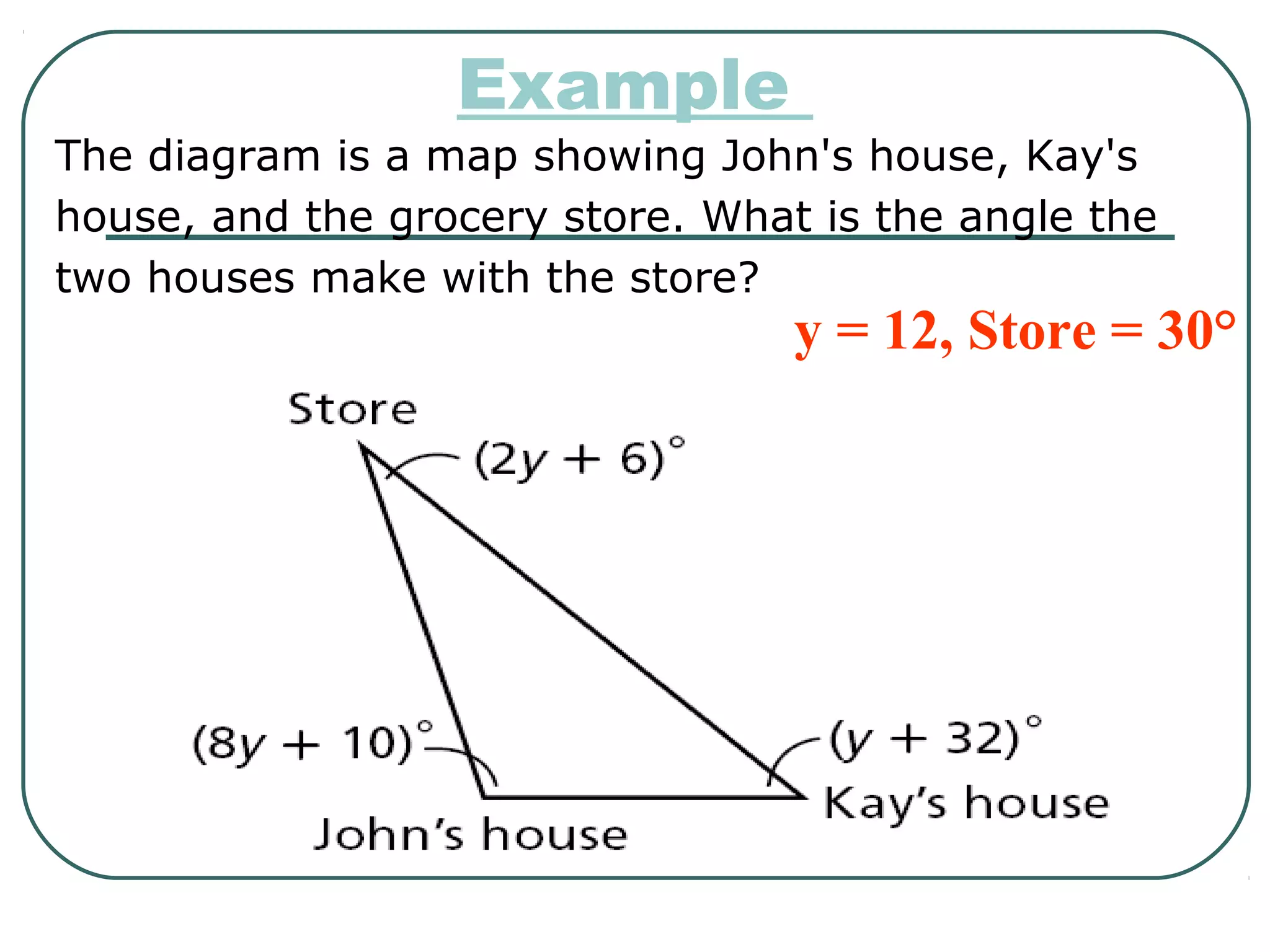
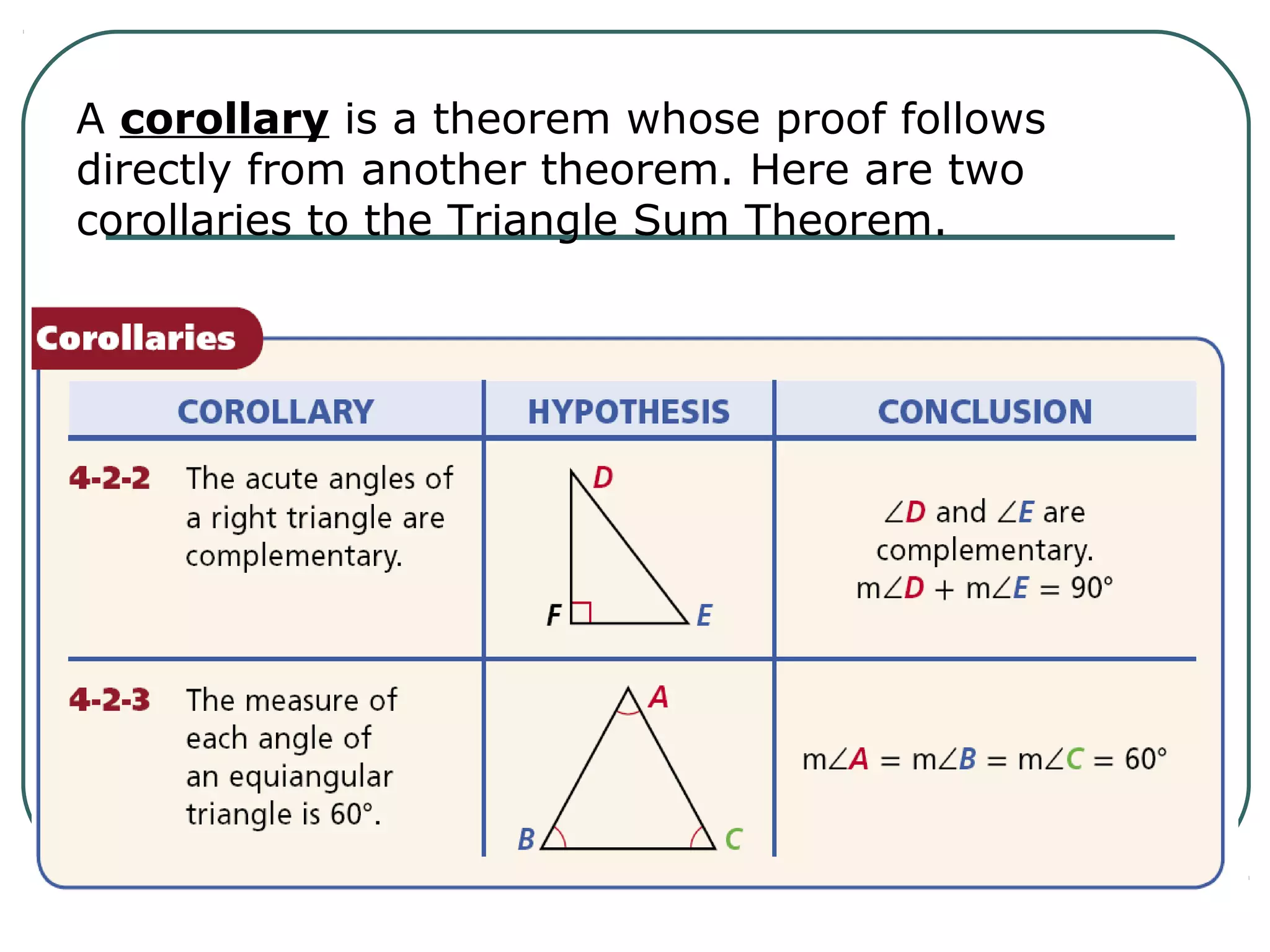
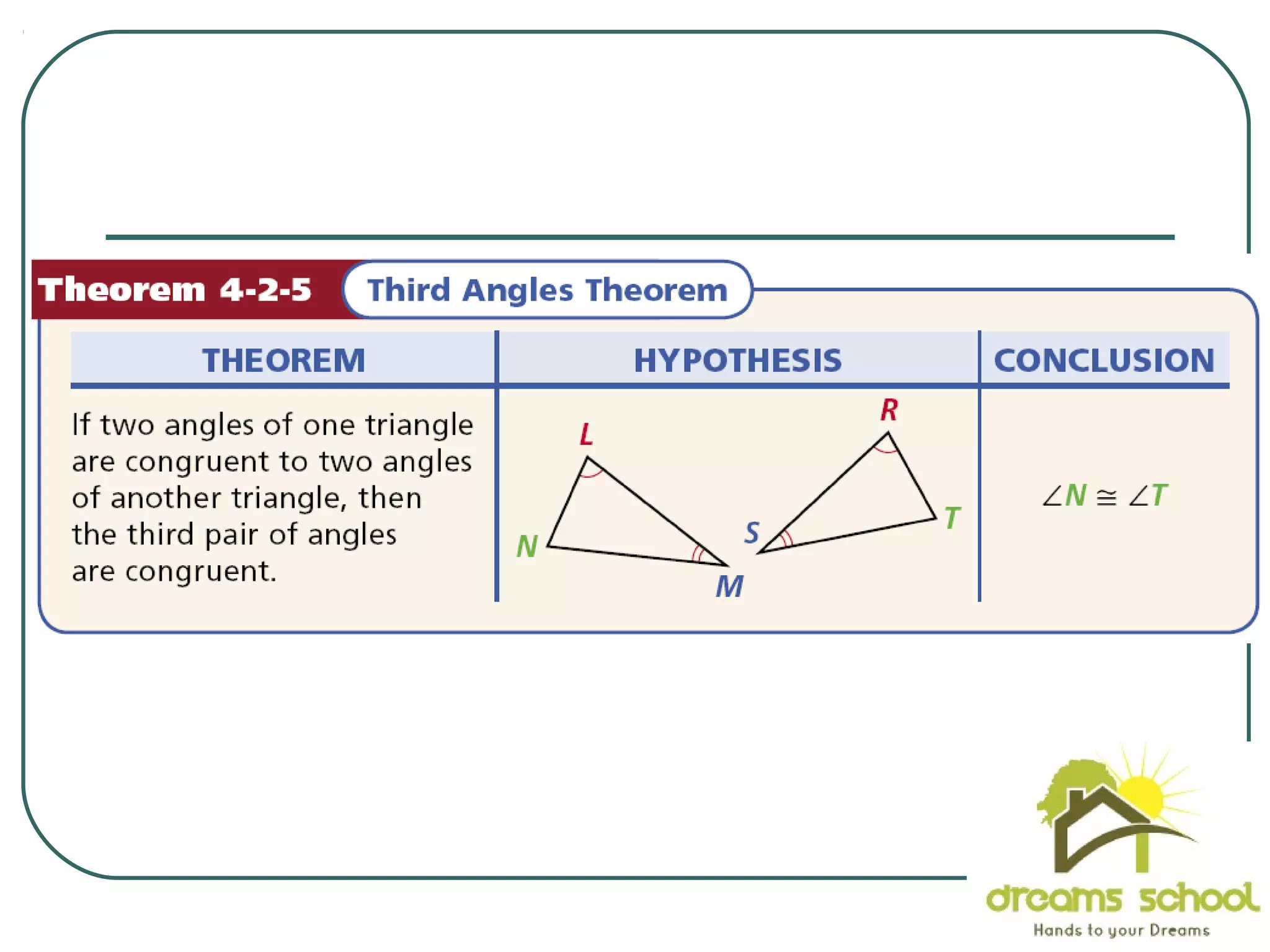
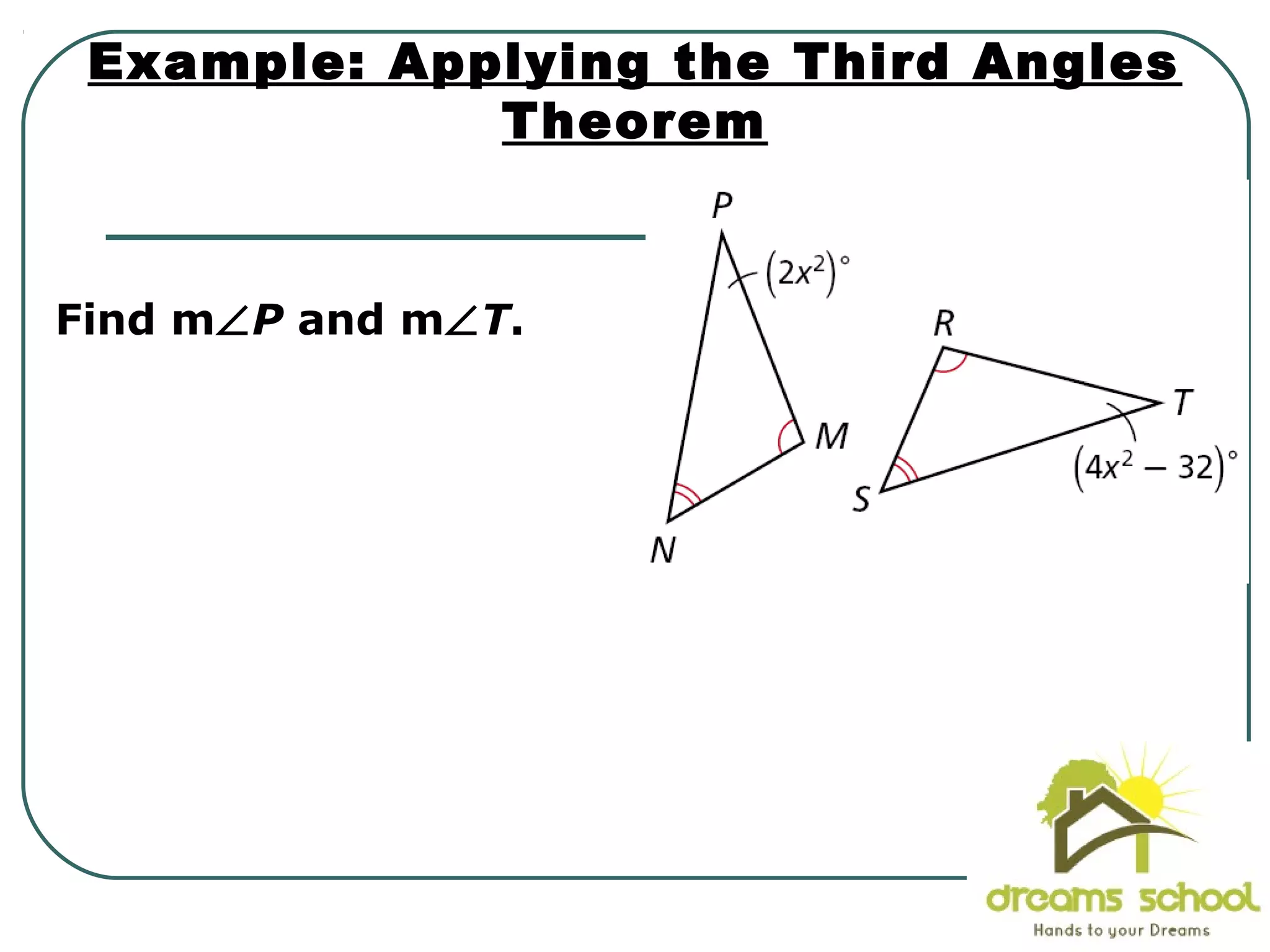
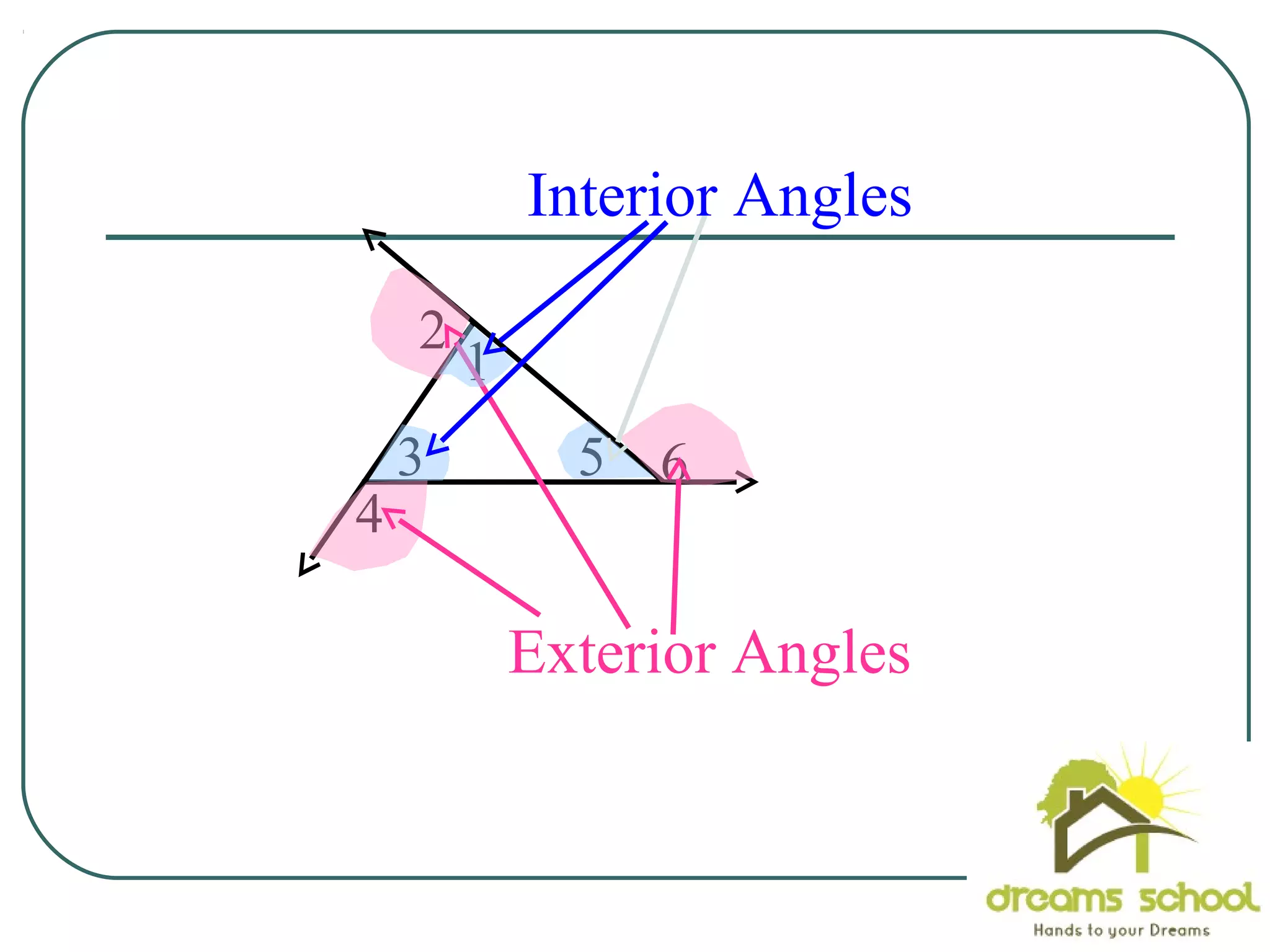
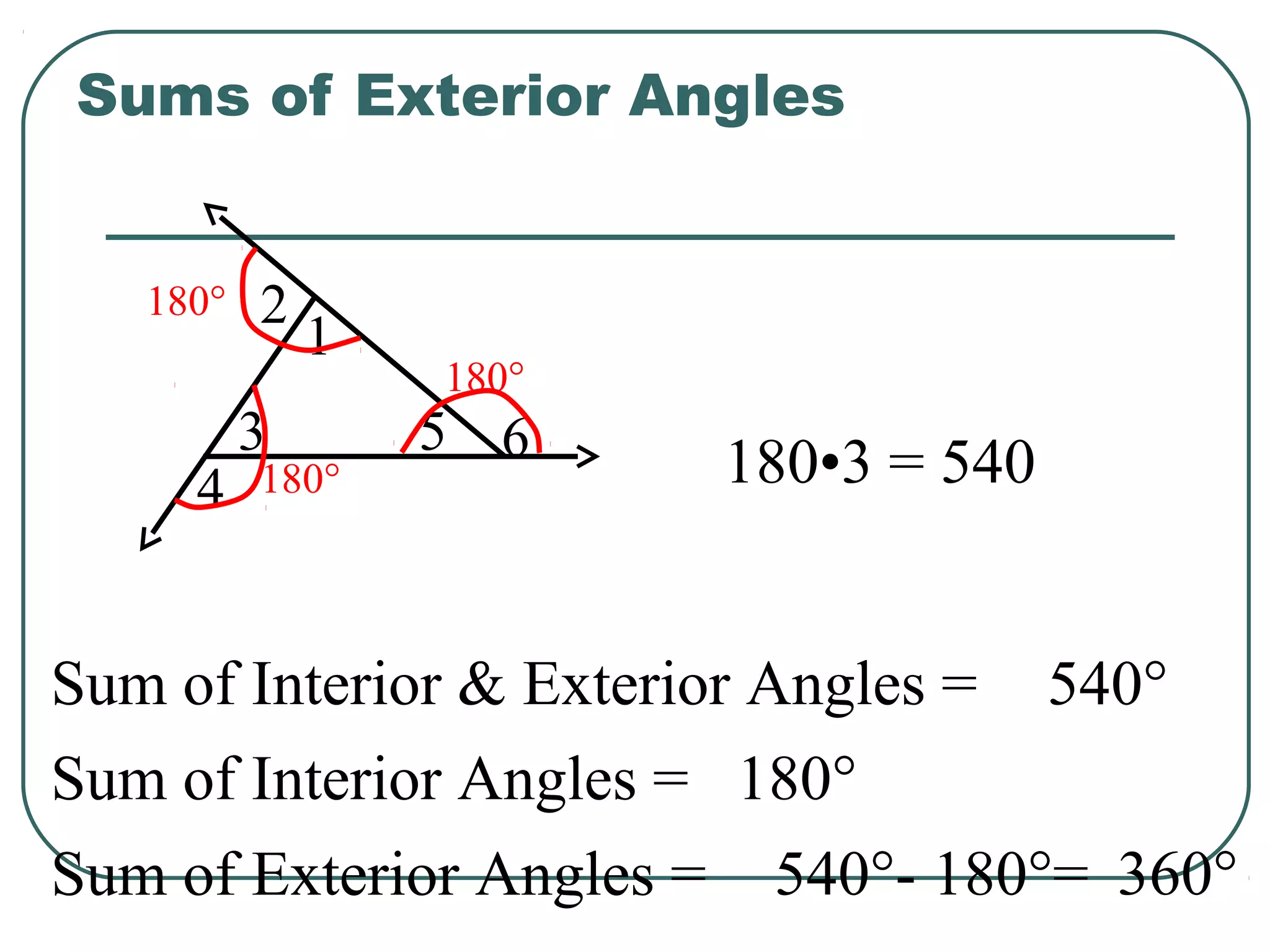
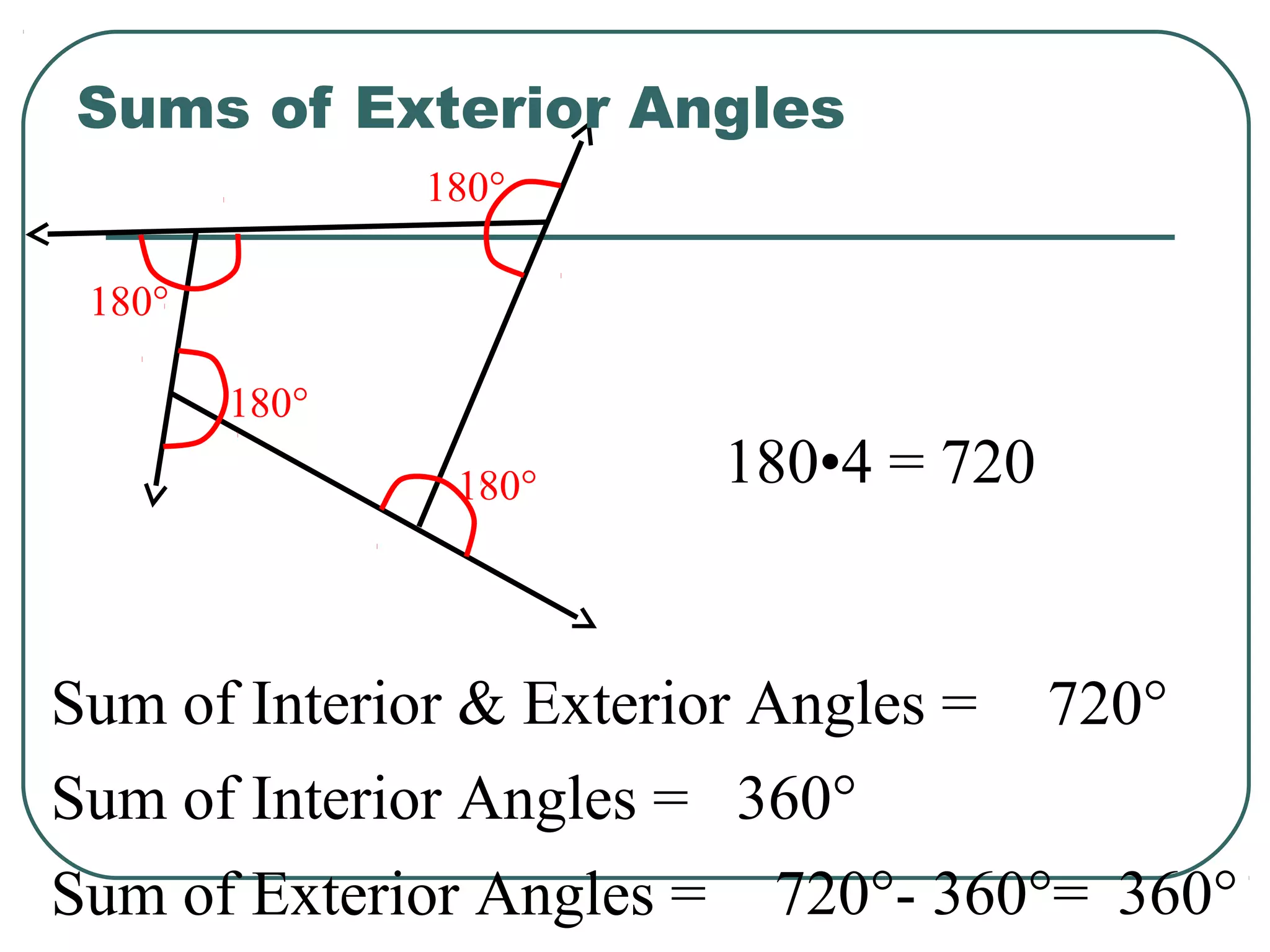
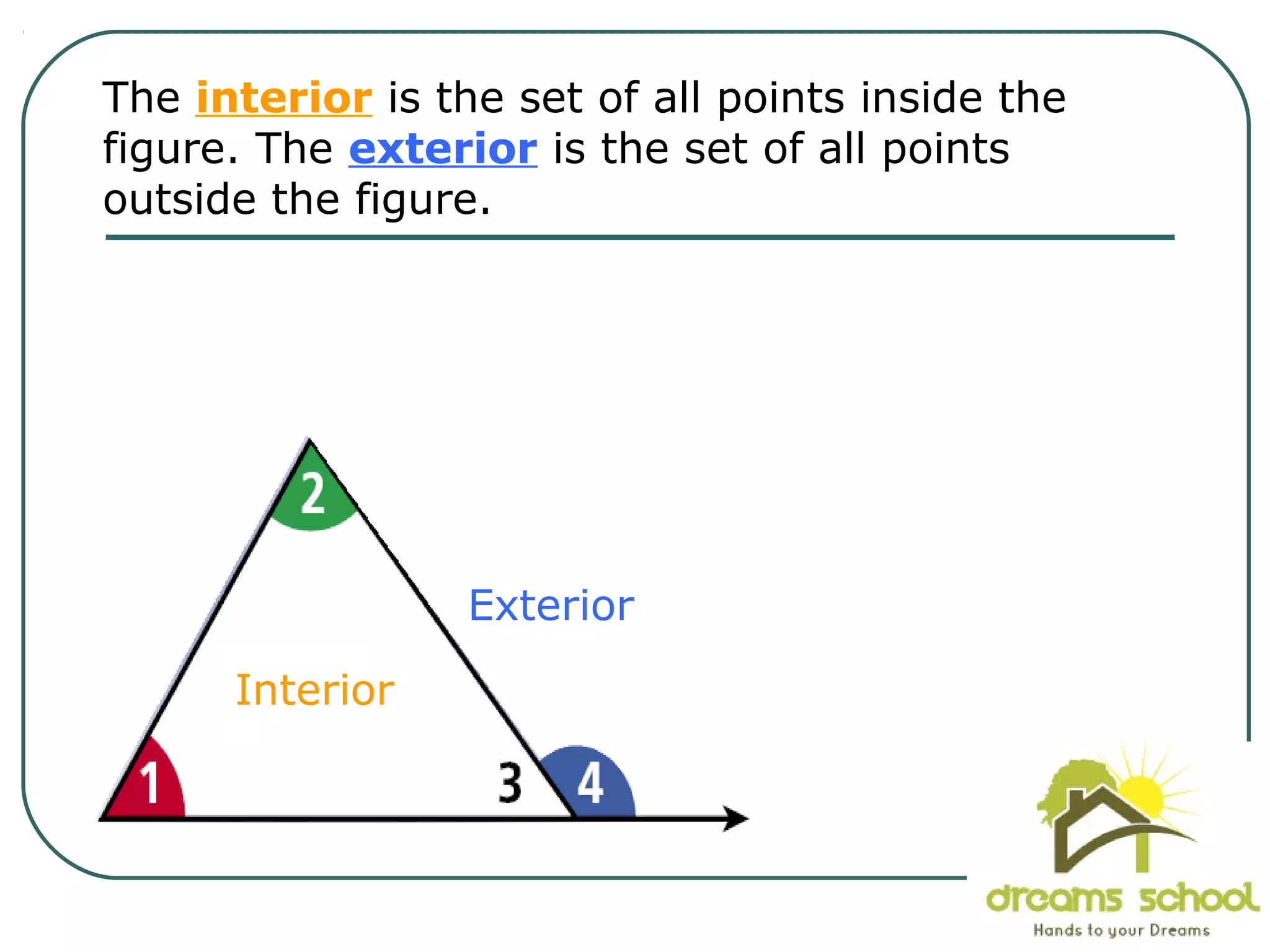
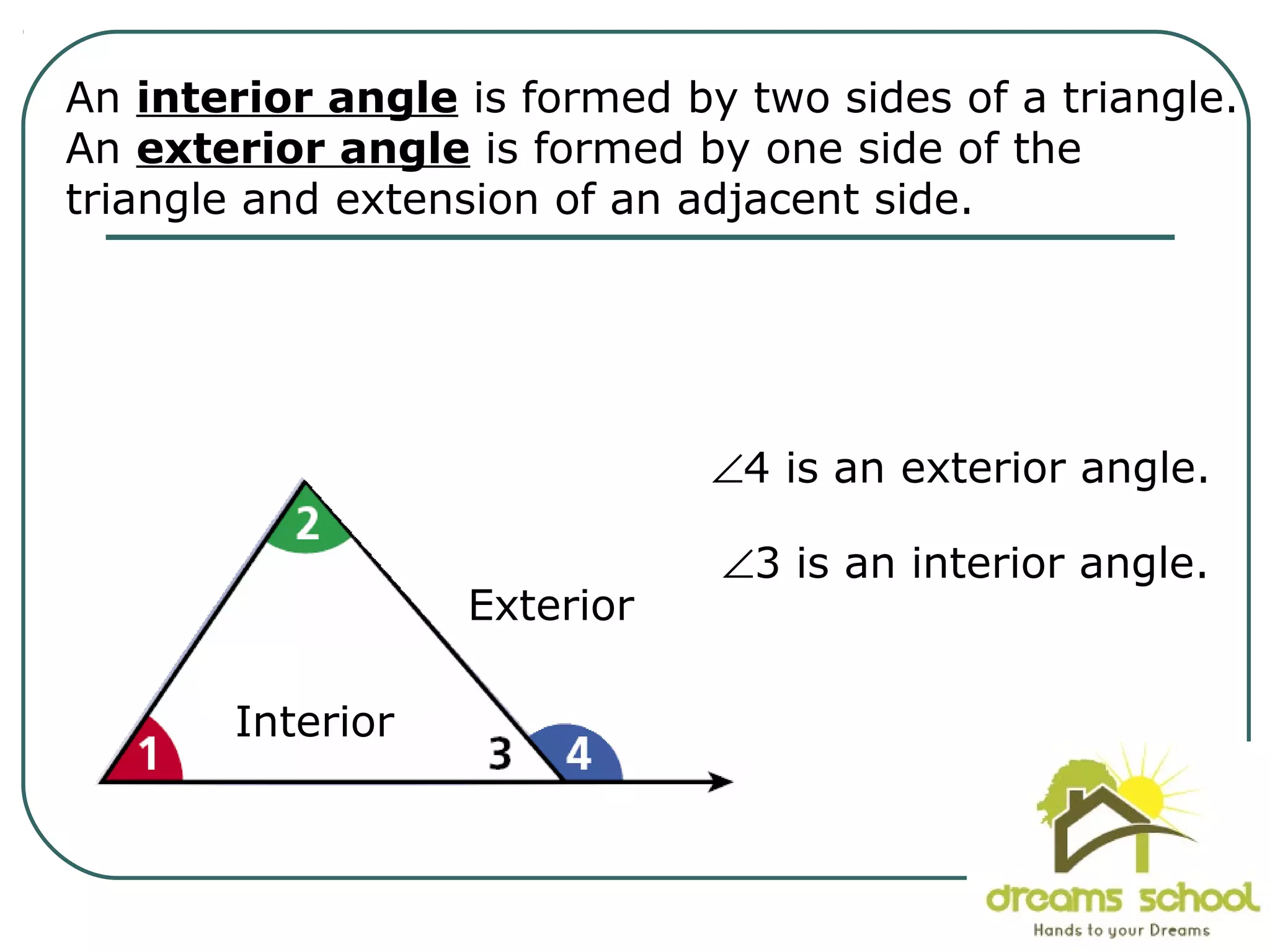
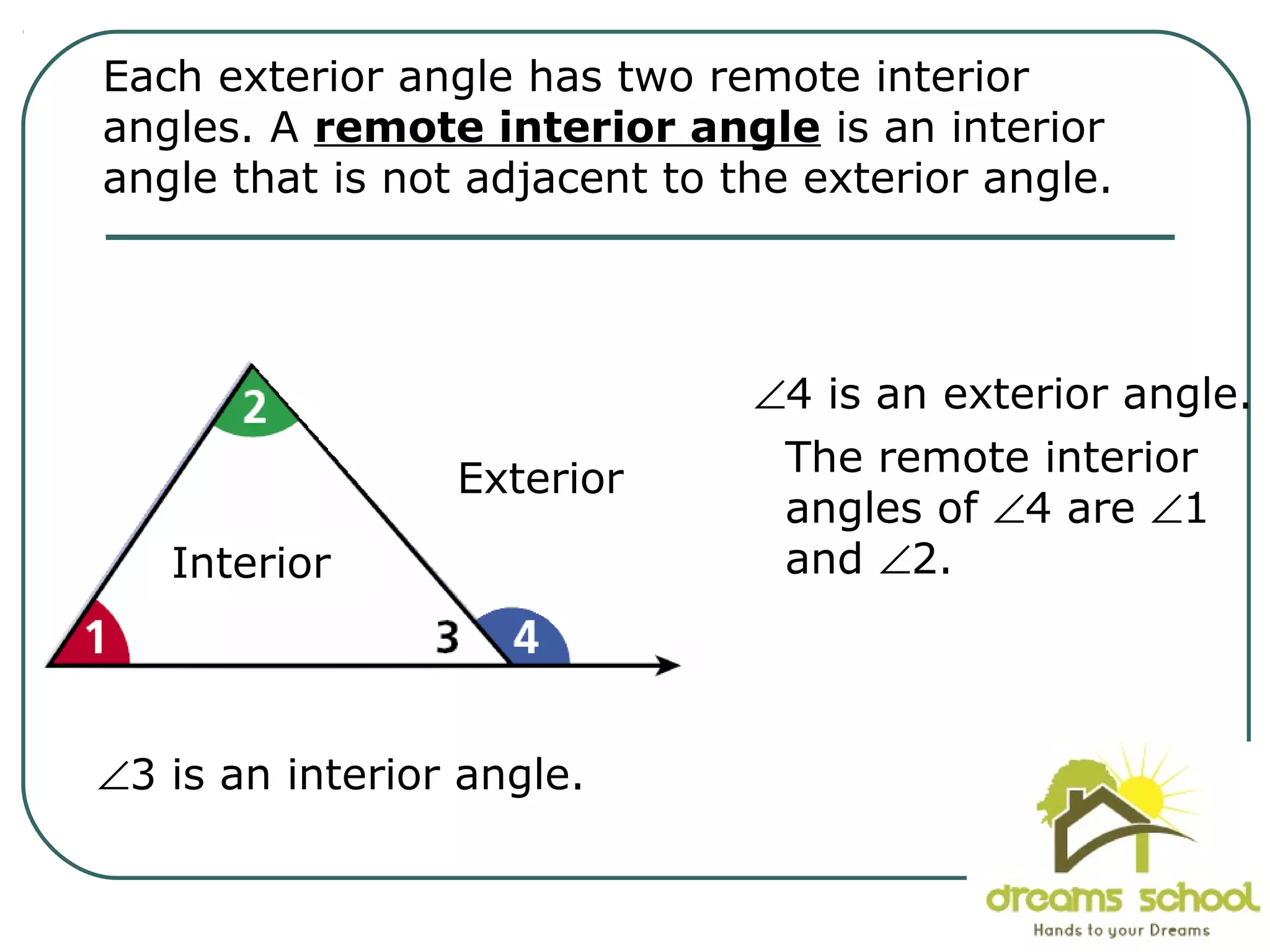
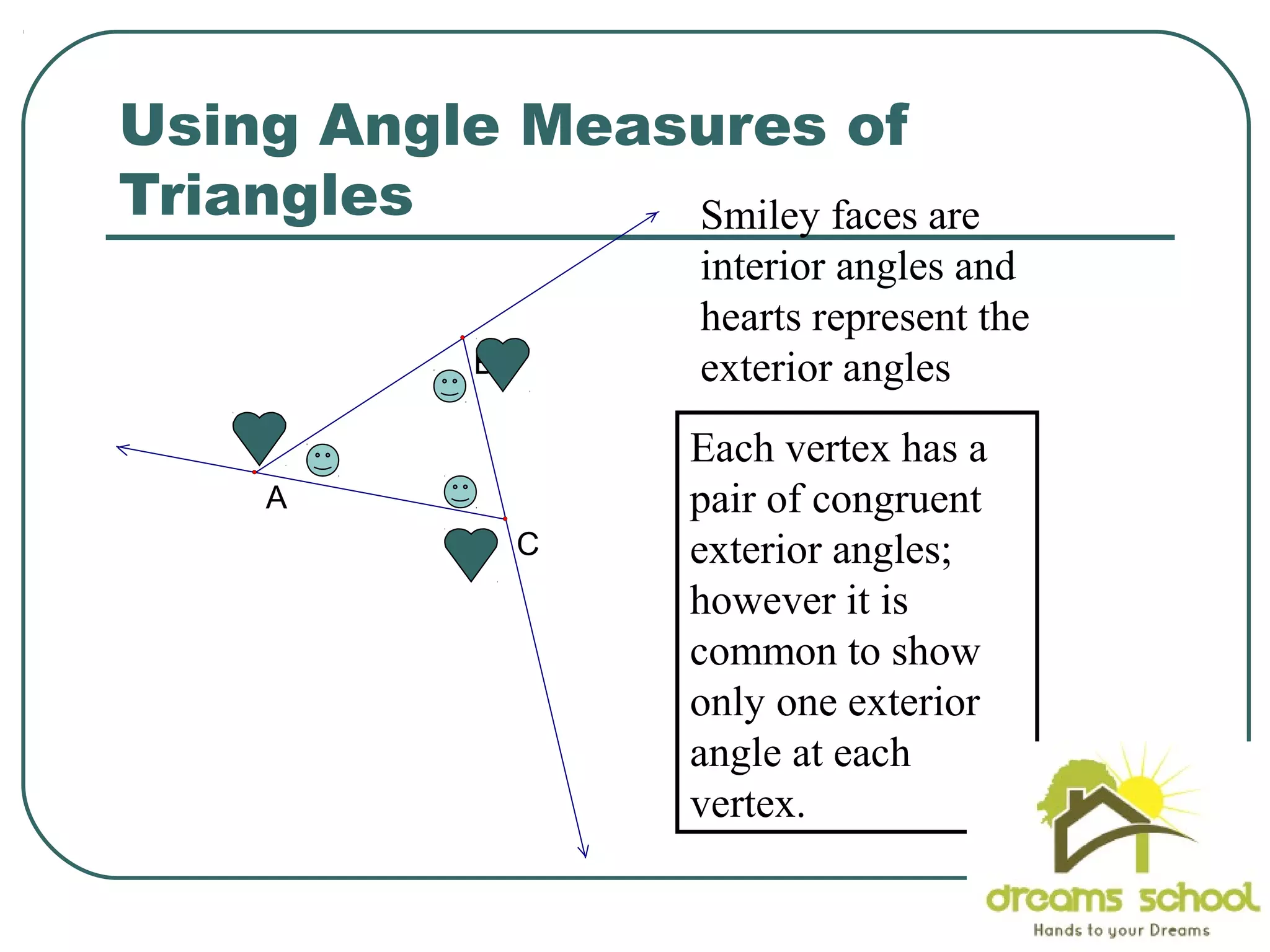
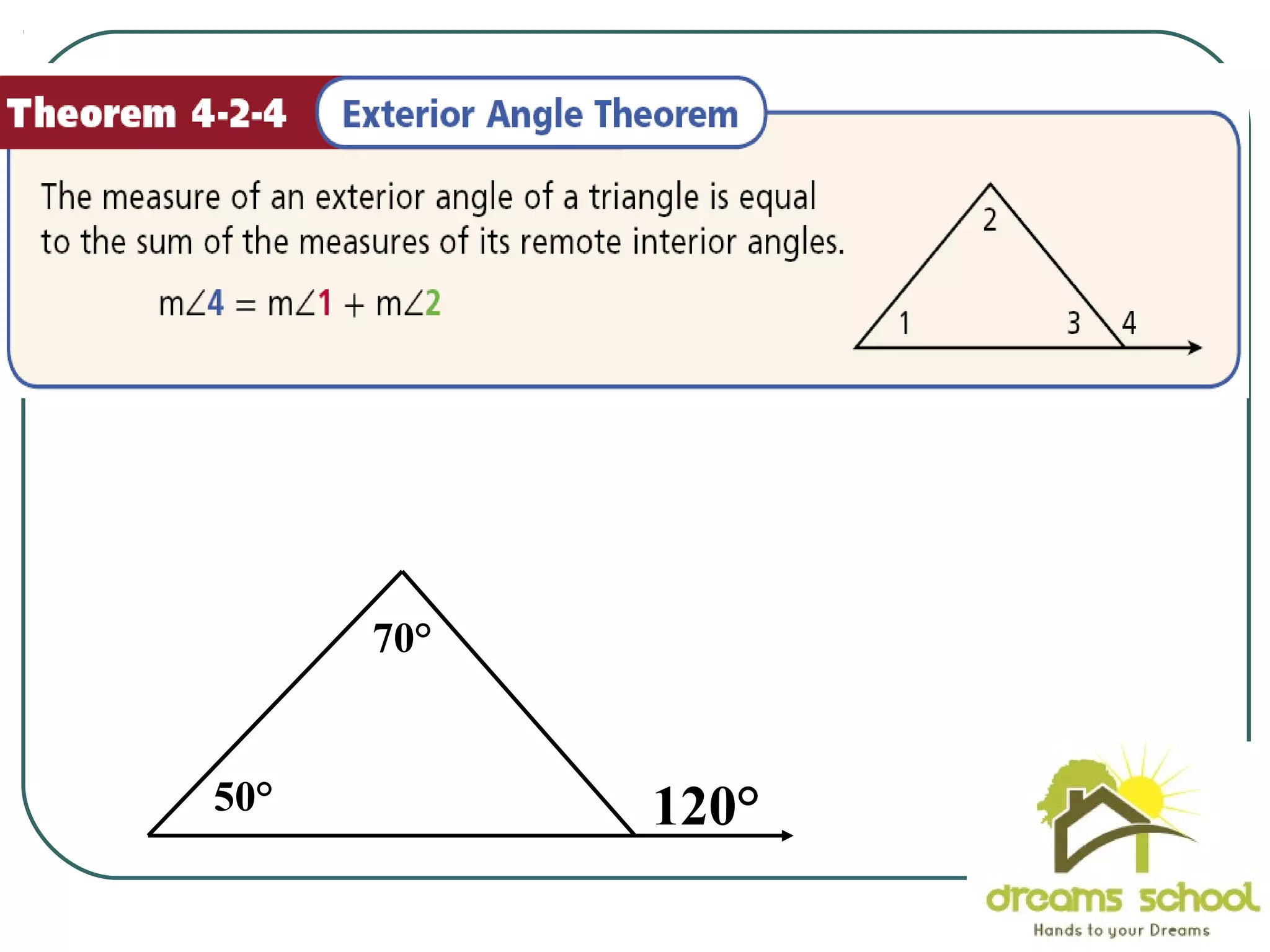
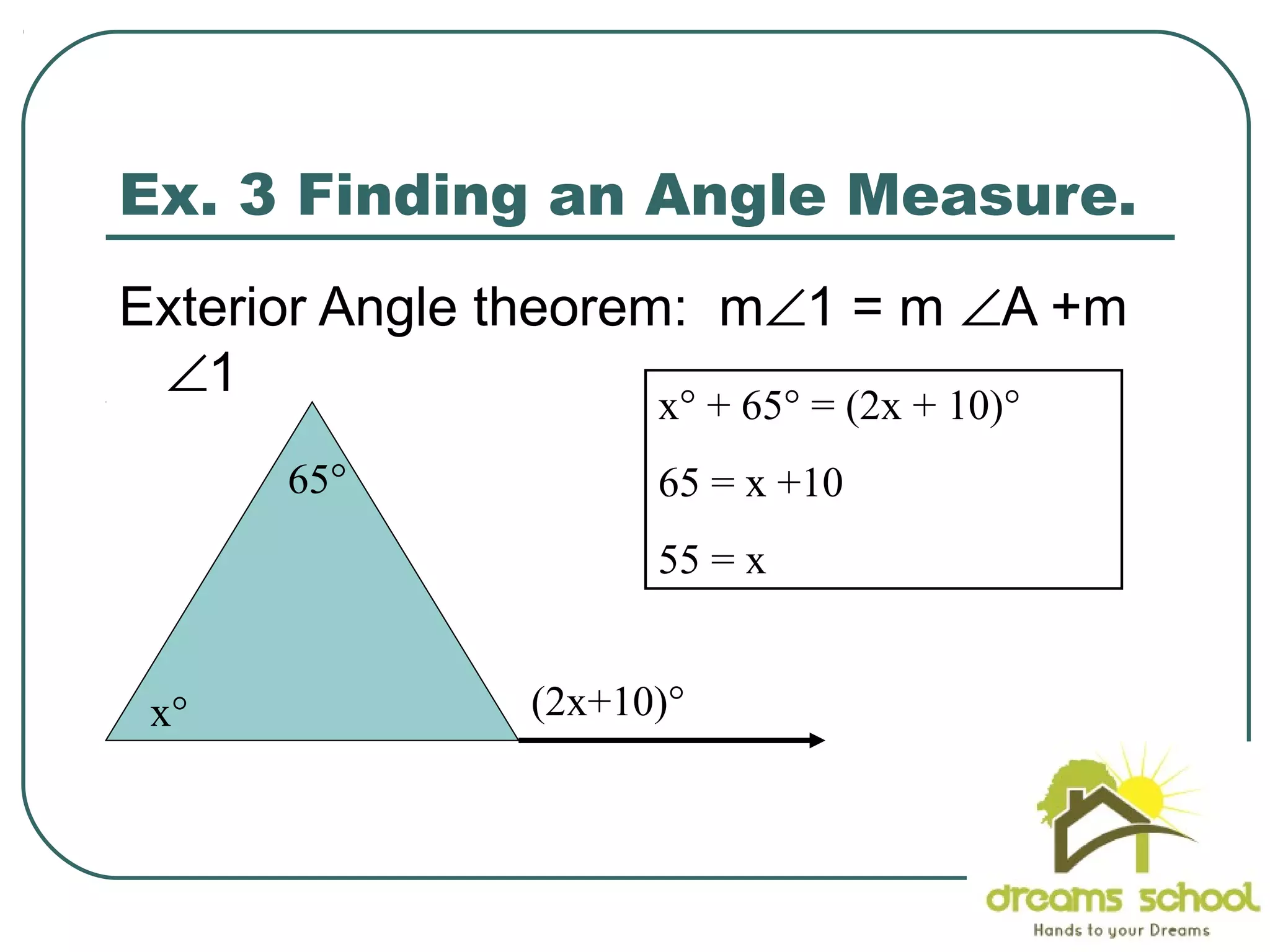
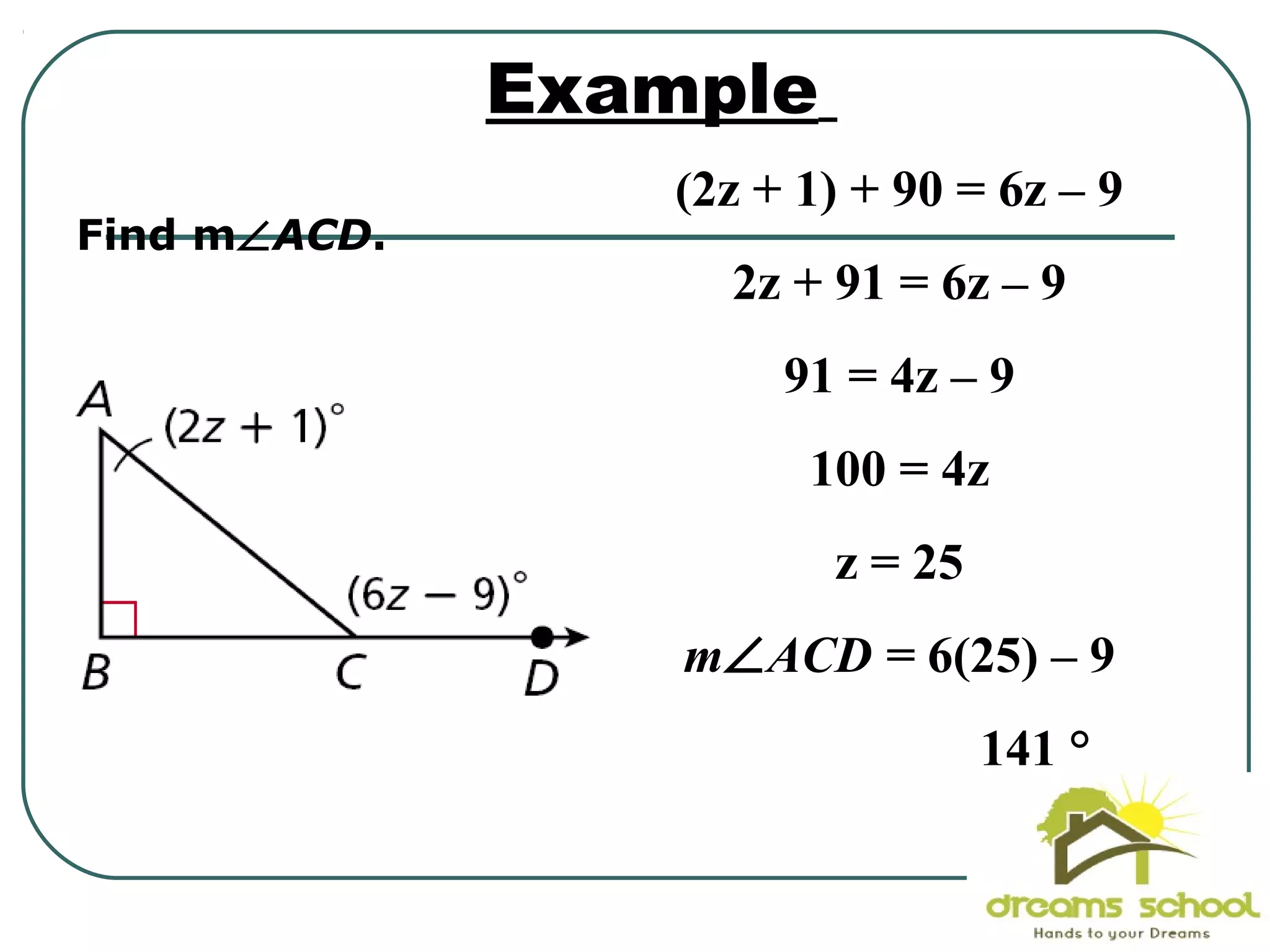
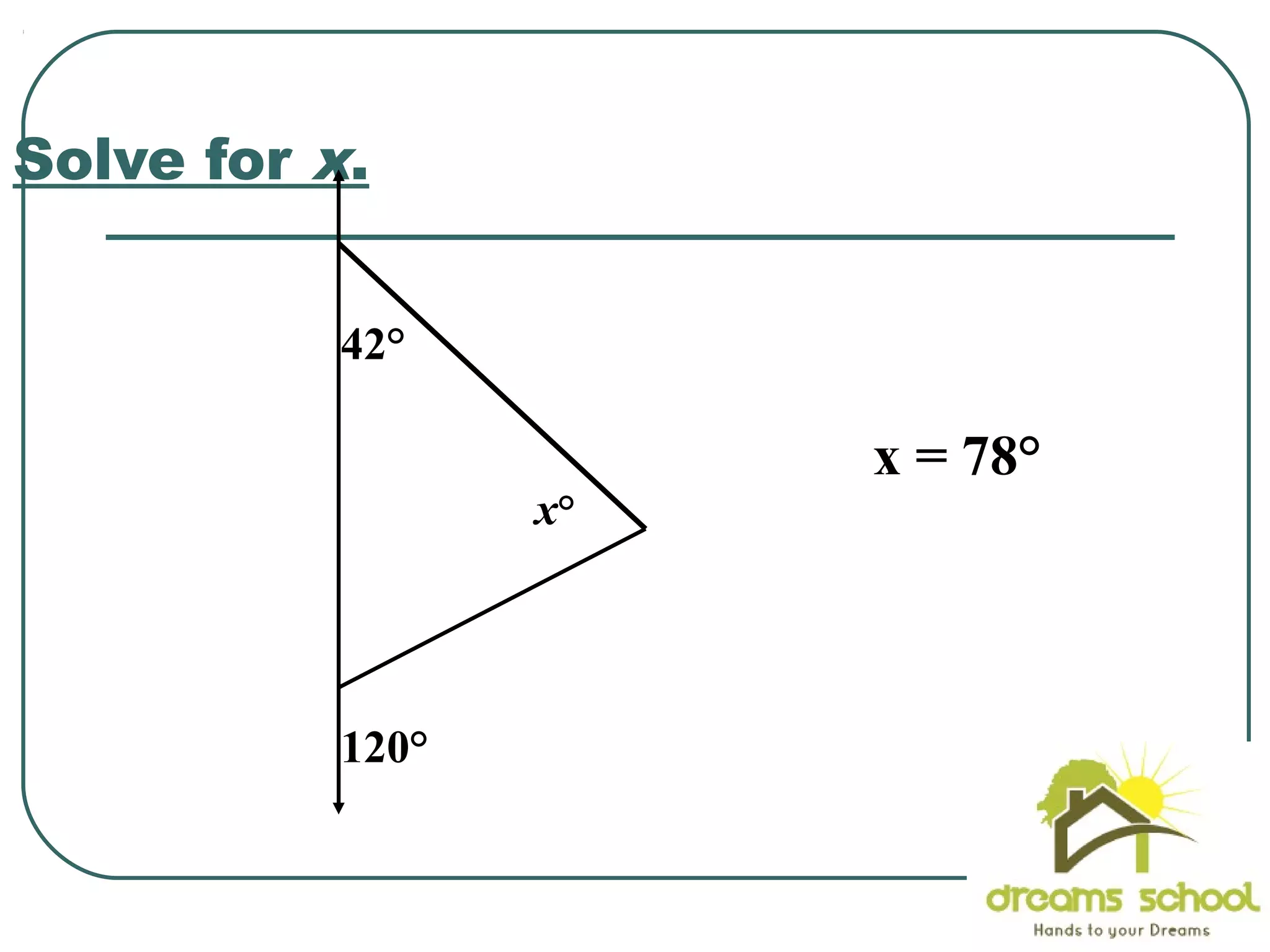
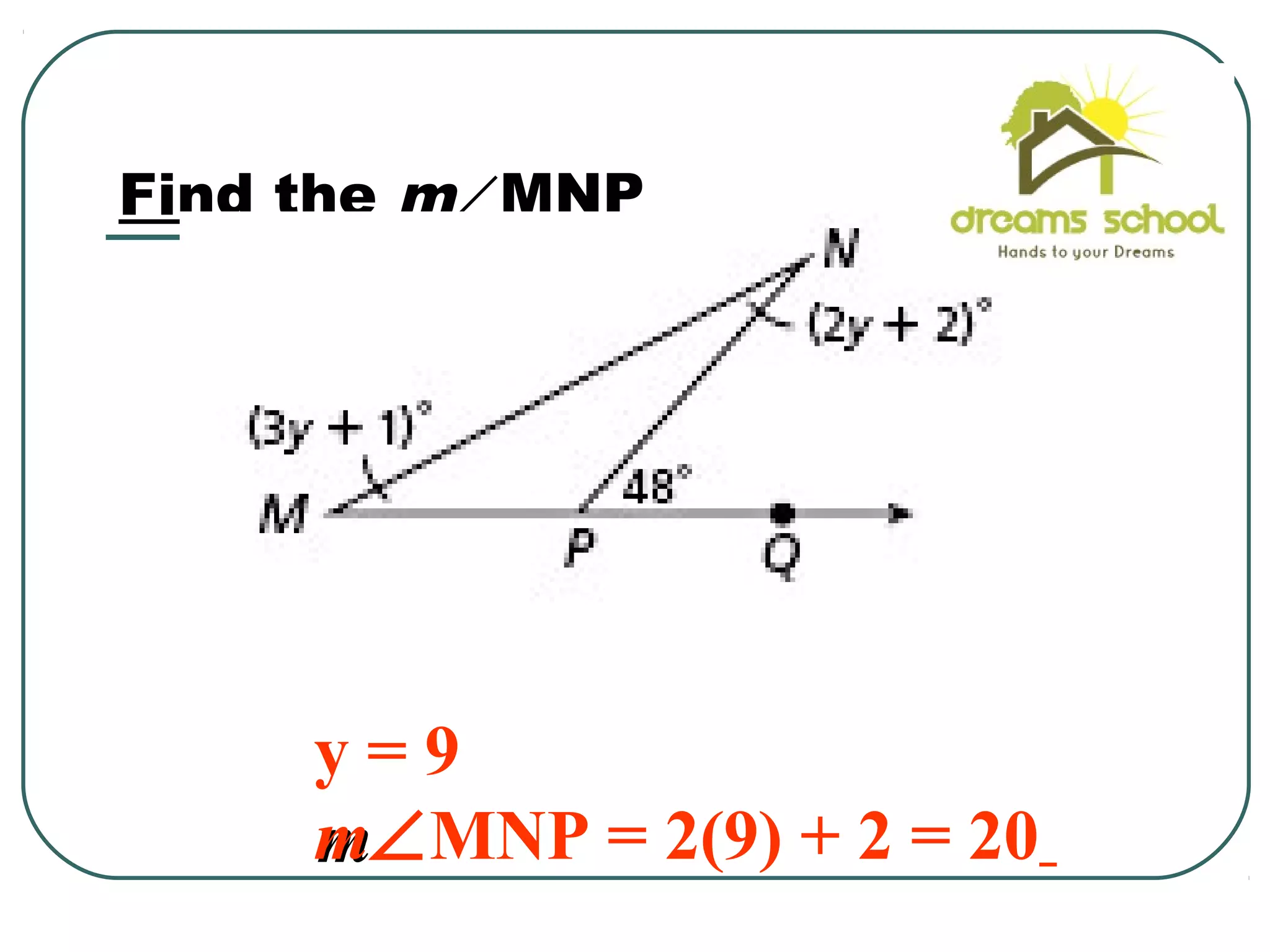
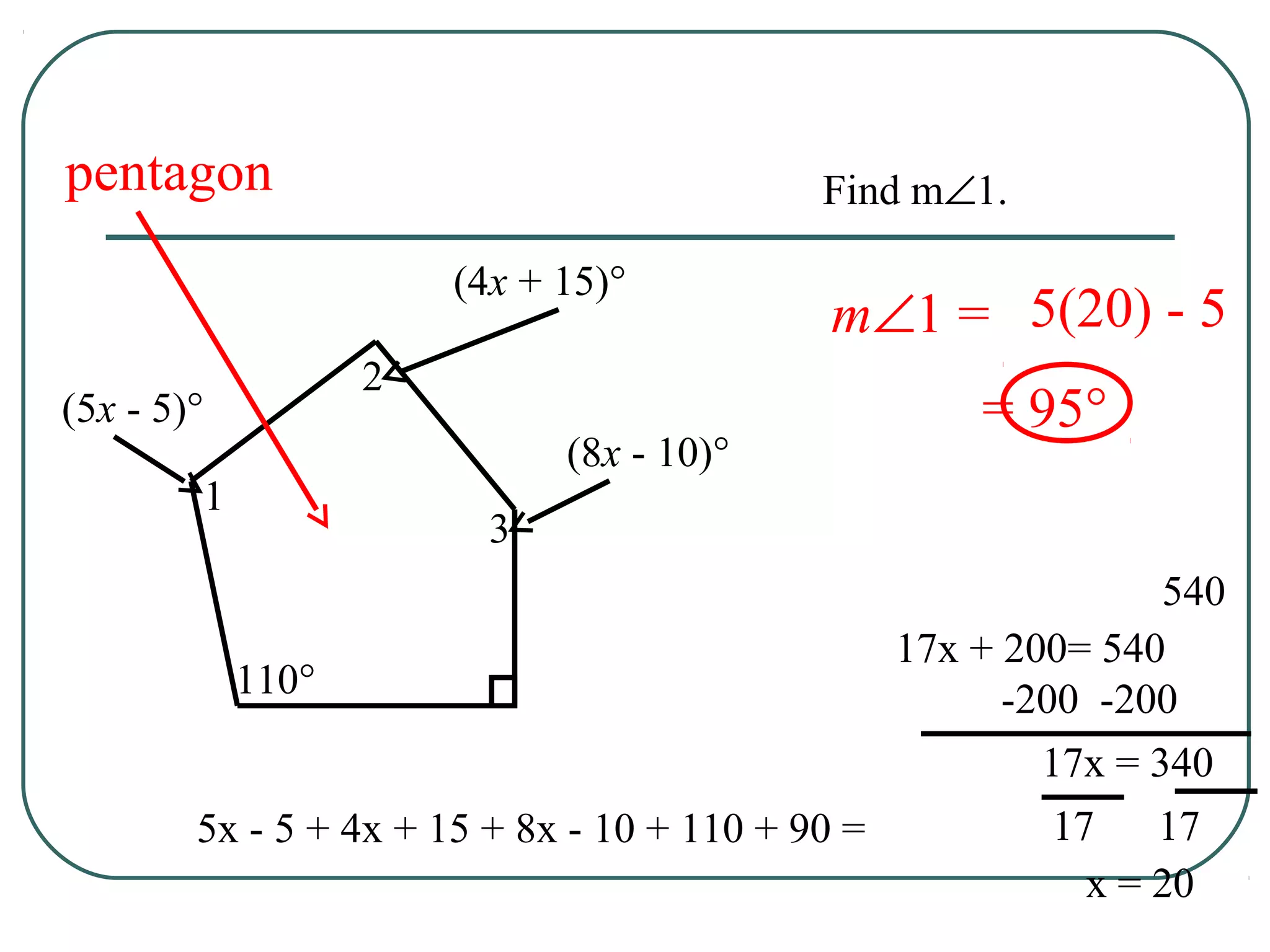
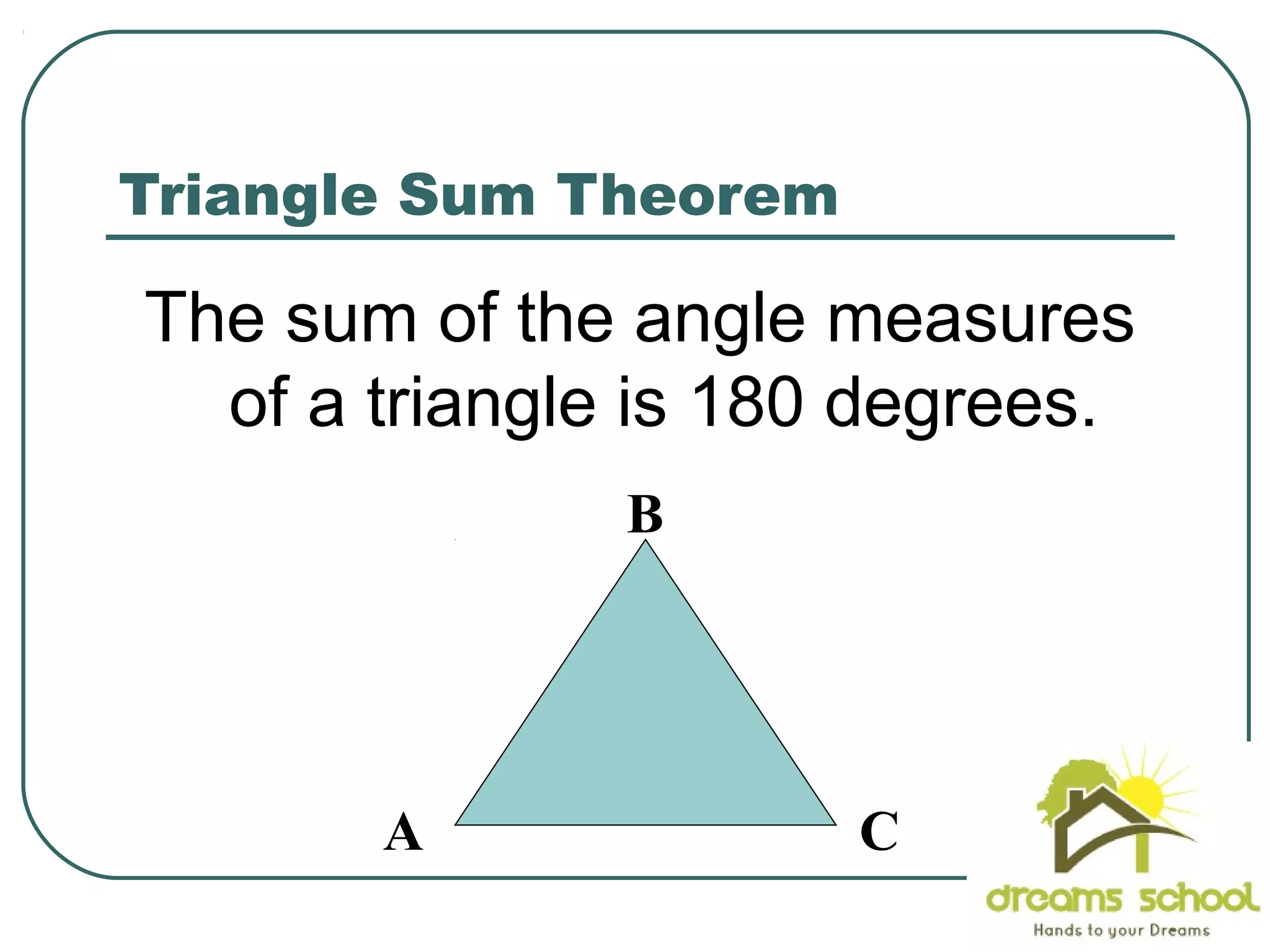
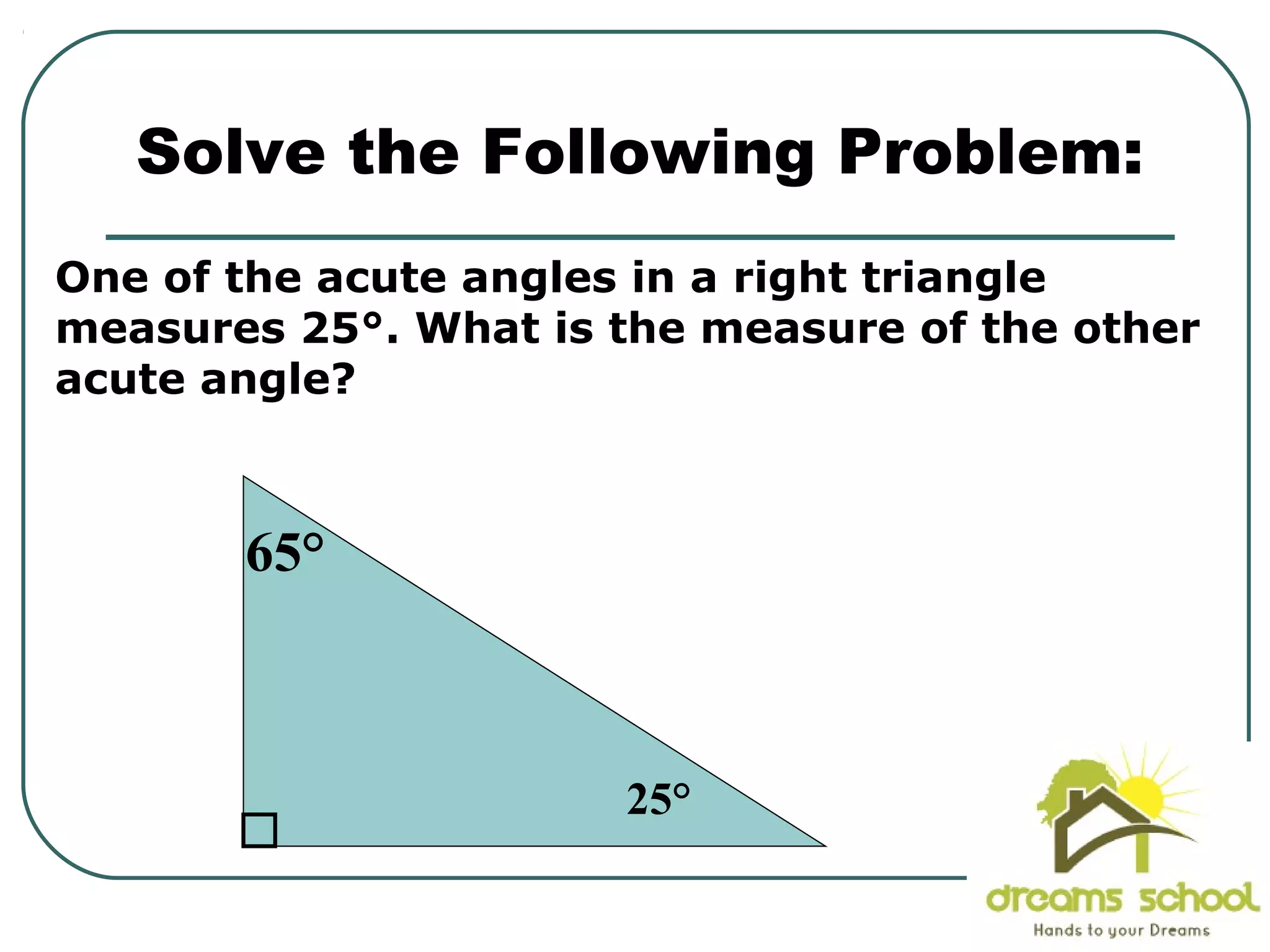
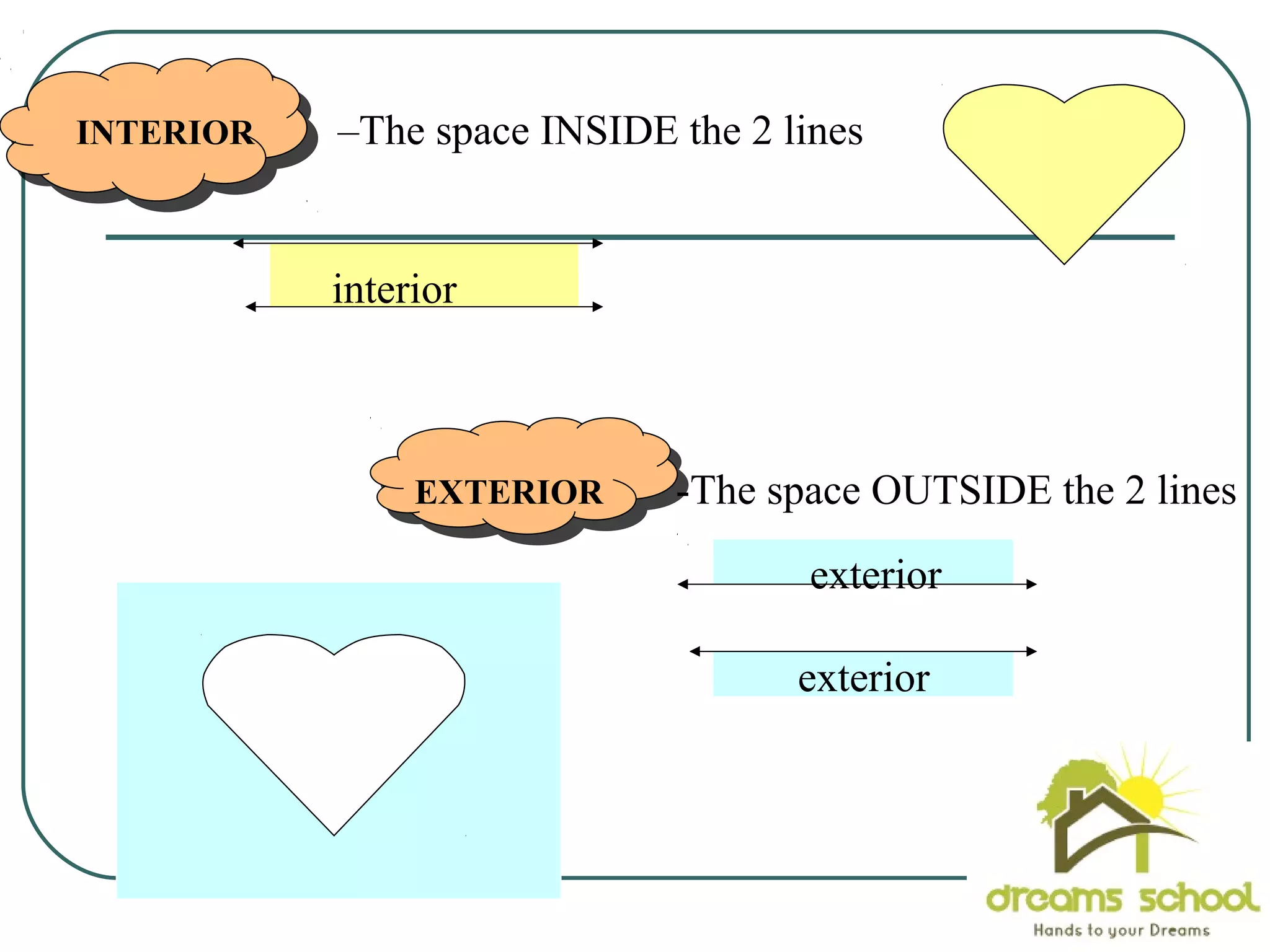
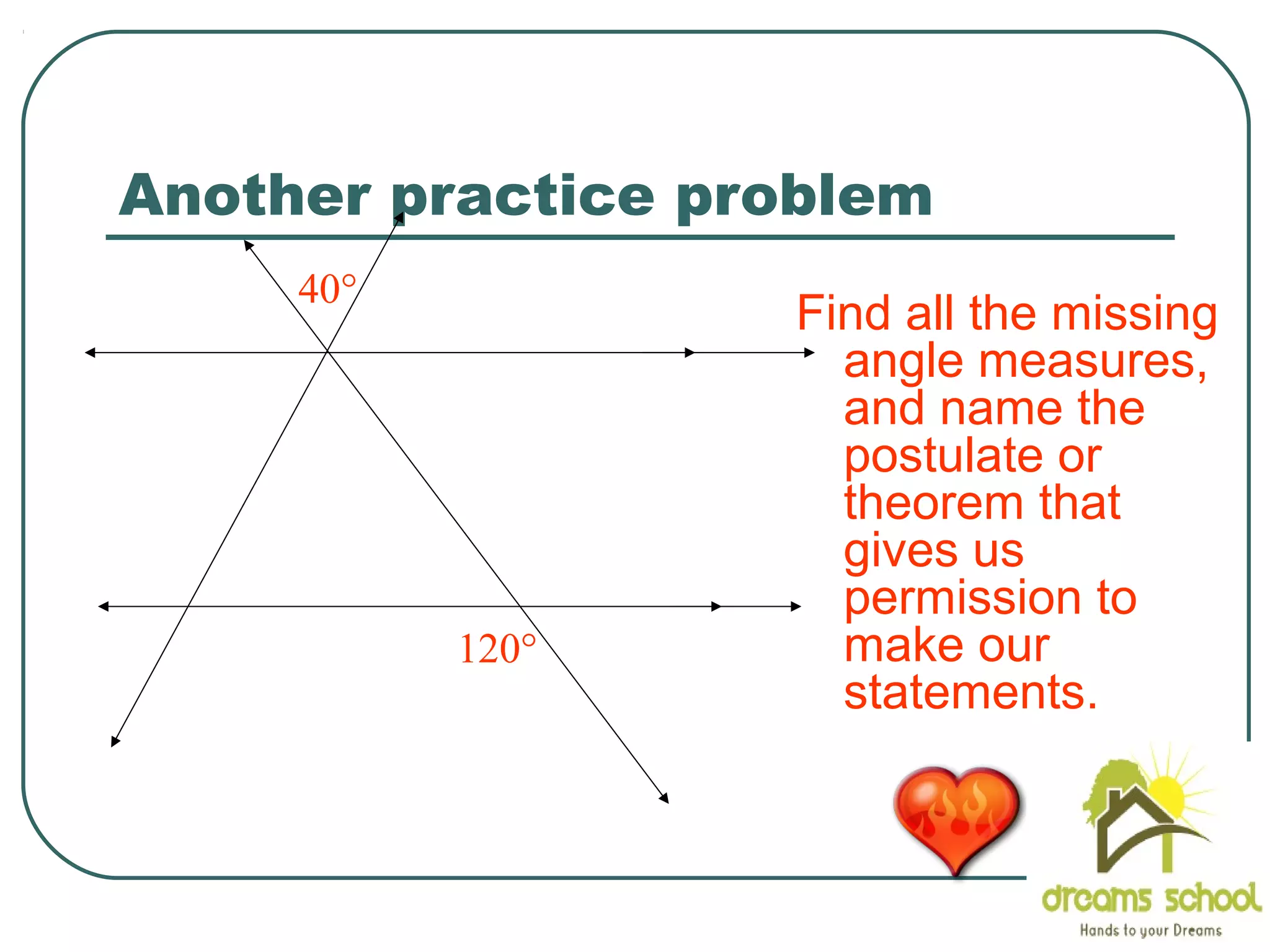
The document provides information about geometry, specifically angles of triangles. It discusses the triangle angle sum theorem, which states that the sum of the interior angles of any triangle is 180 degrees. It provides examples of using this theorem to find missing angle measures in triangles. It also covers exterior angles and their relationships to interior angles, including theorems such as the exterior angle theorem. The document aims to teach students about important angle properties and relationships in triangles through definitions, theorems, and worked examples.

1. Geometry
Angles of Triangles
The Triangle Angle Sum
Theorem
The Exterior Angle Theorem

2. Remember!
When you look at a figure, you cannot assume
segments or angles are congruent based on
appearance. They must be marked as congruent.
IN ADDITION:
 Do not assume anything in Geometry is
congruent – unless they are marked.
 This is true for parallel & perpendicular lines.

3. Triangle Sum Theorem
The sum of the angle measures
of a triangle is 180 degrees.
A
B
C

4. Example – Find the measure
of the missing angle.
46°
91°
43°

5. Example: Find m<1
Find m<2
Find m<3 28
82
682
1
3
m<1 = 70
m<2 = 70
m<3 = 42

6. One of the acute angles in a right triangle
measures 25°. What is the measure of the other
acute angle?
Solve the Following Problem:
25°
65°

7. Example
The diagram is a map showing John's house, Kay's
house, and the grocery store. What is the angle the
two houses make with the store?
y = 12, Store = 30°

8. A corollary is a theorem whose proof follows
directly from another theorem. Here are two
corollaries to the Triangle Sum Theorem.

10. Example: Applying the Third Angles
Theorem
Find m∠P and m∠T.

11. The measure of one of the acute angles in a
right triangle is 63.7°. What is the measure of
the other acute angle?
Example:
26.3°

12. 1
2
3
4
5 6
Exterior Angles
Interior Angles

13. Sum of Interior Angles =
Sum of Interior & Exterior Angles =
180°
1
2
3
4
5 6
180°
180°
180°
540°
Sum of Exterior Angles = 360°540°- 180°=
Sums of Exterior Angles
180•3 = 540

14. 180°
180°
180°
180°
Sum of Interior Angles =
Sum of Interior & Exterior Angles =
360°
720°
Sum of Exterior Angles = 360°720°- 360°=
Sums of Exterior Angles
180•4 = 720

15. The interior is the set of all points inside the
figure. The exterior is the set of all points
outside the figure.
Interior
Exterior

16. An interior angle is formed by two sides of a triangle.
An exterior angle is formed by one side of the
triangle and extension of an adjacent side.
Interior
Exterior
∠4 is an exterior angle.
∠3 is an interior angle.

17. Each exterior angle has two remote interior
angles. A remote interior angle is an interior
angle that is not adjacent to the exterior angle.
Interior
Exterior
∠3 is an interior angle.
∠4 is an exterior angle.
The remote interior
angles of ∠4 are ∠1
and ∠2.

18. 18
A
B
C
Using Angle Measures of
Triangles Smiley faces are
interior angles and
hearts represent the
exterior angles
Each vertex has a
pair of congruent
exterior angles;
however it is
common to show
only one exterior
angle at each
vertex.

19. 70°
50° 120°

20. 20
Ex. 3 Finding an Angle Measure.
65°
x°
Exterior Angle theorem: m∠1 = m ∠A +m
∠1
(2x+10)°
x° + 65° = (2x + 10)°
65 = x +10
55 = x

21. Find m∠ACD.
Example
(2z + 1) + 90 = 6z – 9
2z + 91 = 6z – 9
91 = 4z – 9
100 = 4z
z = 25
m∠ACD = 6(25) – 9
141 °

22. Lesson Review
1. The measure of one of the acute angles in a right
triangle is 56 °. What is the measure of the other
acute angle?
2. Find m∠ABD. 3. Find m∠N and m∠P.
124° 75°; 75°
2
3
33 °
1
3

23. Find m∠B.
Example: Applying the Exterior Angle Theorem
2x + 3 + 15 = 5x – 60
2x + 18 = 5x – 60
18 = 3x – 60
78 = 3x
x = 26
m∠B = 2(26) + 3
m∠B = 55°

24. Solve for x.
42°
x°
120°
x = 78°

25. Find the m∠MNP
y = 9
mm∠MNP = 2(9) + 2 = 20

26. m∠1 =
1
2
3
110°
(5x - 5)°
(4x + 15)°
(8x - 10)°
pentagon
5x - 5 + 4x + 15 + 8x - 10 + 110 + 90 =
540
17x + 200= 540
-200 -200
17x = 340
x = 20
17 17
5(20) - 5
= 95°
Find m∠1.

27. Triangle Sum Theorem
The sum of the angle measures
of a triangle is 180 degrees.
A
B
C

28. Example – Find the measure
of the missing angle.
46°
91°
43°

29. One of the acute angles in a right triangle
measures 25°. What is the measure of the other
acute angle?
Solve the Following Problem:
25°
65°

30. Angle Relationships
Lesson 2-1 angles relationships 31

31. interior
INTERIOR –The space INSIDE the 2 lines
EXTERIOR -The space OUTSIDE the 2 lines
exterior
exterior

32. Another practice problem
Find all the missing
angle measures,
and name the
postulate or
theorem that
gives us
permission to
make our
statements.
40°
120°

33. 37
Do you find this slides were useful?
One second of your life , can bring a smile in a girl life
If Yes ,Join Dreams School “Campaign for Female
Education”
Help us in bringing a change in a girl life, because “When
someone takes away your pens you realize quite how
important education is”.
Just Click on any advertisement on the page, your one
click can make her smile.
Eliminate Inequality “Not Women”
One second of your life , can bring a smile in her life!!
Do you find these slides were useful?
If Yes ,Join Dreams School “Campaign
for Female Education”
Help us in bringing a change in a girl life,
because “When someone takes away your
pens you realize quite how important
education is”.
Just Click on any advertisement on the page,
your one click can make her smile.
We our doing our part & u ?
Eliminate Inequality “Not Women”