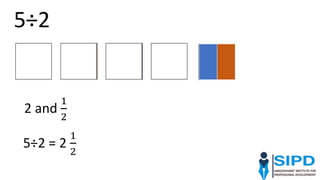
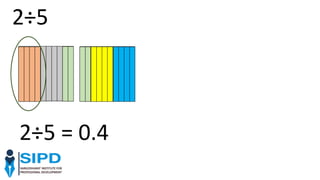
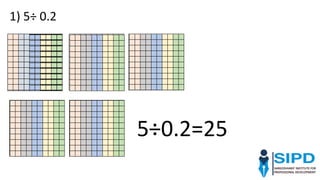
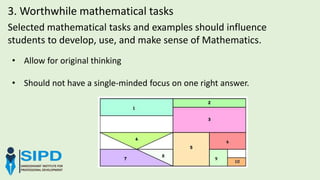
The document discusses effective approaches to teaching mathematics, highlighting the need to move away from traditional 'chalk and talk' methods towards more interactive and student-centered learning experiences. It emphasizes building on students' existing knowledge, fostering independent and collaborative thinking, and creating worthwhile mathematical tasks that encourage original thought and connections to real-life situations. The role of the teacher is crucial in facilitating discussions, managing classroom dynamics, and using students' misconceptions as stepping stones for deeper understanding.

1. Math Teaching
Approaches That Work
With
Muhammad Yusuf
Welcome!

2. 2
Web: www.sipd.org.pk
Facebook: https://web.facebook.com/Sargodhians-Institute-for-Professional-Development-
101446921620638/
Twitter: https://twitter.com/officialSIPD
LinkedIn: http://www.linkedin.com/in/sipd
Slide share: https://www.slideshare.net/SSIPDRashidabad
YouTube:
https://www.youtube.com/channel/UCe78ohzbv4LEfM_lwlqdyuw?view_as=subscriber

3. Let us start with some important point about teaching and learning
mathematics

4. But unfortunately,
Many students struggle with mathematics and become disaffected as
they continually encounter obstacles to engagement.

5. Why this happens

6. Chalk and talk are the most popular methods/pedagogy used in
Mathematics Class.
Why this happens
Teachers Students
Teaching?
Learning?
Yes
Yes
Yes
?

7. So, we need to
break this pattern

8. Arranging for learning
Provide opportunities for
individual and
collaborative work to
make sense of ideas.

9. i) Independent thinking time.
Arranging for learning
It helps to grasp a new concept or
solve a math problem without
distracted by other views.
Provide opportunities to the learners
to think and work quietly by
themselves.

10. Arranging for learning
ii) Whole class discussion
• Invite students to explain their solutions to
others
• Encourage students to listen to and respect one
another, accept and evaluate different
viewpoint
• Teacher role: Manage, moderate, monitor
students' participation, and record students’
solutions.

11. iii) Peer and small groups
Arranging for learning
It helps students
• To see themselves as mathematics learners.
• To clarify the nature of a task and find a possible solution.
• To discussion and test ideas and encourage higher-order thinking
• To make a conjecture and participate in Mathematical
argumentation and validation
Teacher role: Ensure that students understand and follow their roles –
listening, writing, answering, questioning, and assessing.

12. 2. Building on students’ existing experience.
The effective teacher
considered students’
current knowledge and
interest at the focus of
their instructional process.

13. i) Connecting learning to what students are thinking
2. Building on students’ existing experience
In the classroom, students’ thinking is considered as “understanding in
progress”. So, teachers should use students’ thinking as a useful resource for
further learning.
Even Ops. Odd Result
6 + 9 15
10 + 13 23
12 + 5 17
8 + 15 23
2 + 7 9
T: Could any of you tell me, what are you observing in first table?
T: [some students raised their hands], yes, you want to tell us? Yes, Shanawaz?
S1: all answers are odd numbers.
T: Ok, all the answers are coming in odd numbers. So, what can we say in result?
Silence
T: we can say that even plus odd, what will always come?
Ss: Sir, odd.
T: So, we can conclude that if we add any even number with odd number, the
answer should be
Ss: Odd. [Few students together.]

14. As a mathematics teacher, pose new questions or design new tasks that
will challenge and extend thinking.
2. Building on students’ existing experience
i) Connecting learning to what students are thinking
For example:
It takes a machine about 4 minutes to cut 20m2 grass field. How long should it take if
to cut 120m2 grass field?
As you found a student/group solved this problem by using additive thinking,
4⇒20
8⇒40
12⇒60
16⇒80
20⇒100
24⇒120
How long should it take a machine to cut 120m2 grass field it cut about 5m2 grass
field in 1 minute.

15. 2. Building on students’ existing experience
ii) Use students’ misconceptions and errors as building blocks.
Learners make mistakes,
Insufficient time
Care
But errors are
Consistent, and alternative understandings of
mathematical ideas.
So,
What should we do as mathematics teachers?
Wrong thinking VS
as a natural process of students’
conceptual development

16. Ways to address errors
2. Building on students’ existing experience
 Organize whole class or one-to-one discussion that focuses
students’ attention on the targeted concept.
 Share their solution strategies so that they can compare and re-
evaluate students’ thinking.
 To pose questions that they need to be resolved.

17. For example
Confronted with the division misconception, a
teacher may ask students to investigate the difference
between 5÷2, 2÷5, and 5÷0.2 by using diagrams or
pictures.
Continue…

18. 5÷2
2 and
1
2
5÷2 = 2
1
2

19. 2÷5
2÷5 = 0.4

20. 1) 5÷ 0.2
5÷0.2=25

21. 2. Building on students’ existing experience
iii) Appropriate challenge
For example
Reduce the complexity of the task for low achieving students
How long should it take a machine to cut 120m2 grass field
it cut about 5m2 grass field in 1 minute?
Increase the challenge by putting obstacles in the way of solutions,
It takes a machine about 4 minutes to cut 20m2 grass field.
How long should it take if to cut 120m2 grass field?
An effective mathematics teacher gives modified tasks to
provide alternative pathways to understanding on students
existing thinking

22. 3. Worthwhile mathematical tasks
Selected mathematical tasks and examples should influence
students to develop, use, and make sense of Mathematics.
• Allow for original thinking
• Should not have a single-minded focus on one right answer.

23. 1. Mathematical Focus
3. Worthwhile mathematical tasks
The worthwhile mathematical task involves students
making use of formulas, algorithms, and procedures in
ways that connect to concepts and understanding of
meanings.
Example:
Mona worked from 8:15 A.M. to 5:30 P.M. on Monday. She
spent 45 min at lunch. She was told she had worked only for 7
hours. Mona disagrees and asked HR to check her time card.
Who was correct?

24. Fact: worked from 8:15 A.M to 5:30 P.M. had lunch for 45 Minutes.
Question: How long did Mona work on Monday?
Step 1: To find the time difference between 8:15 A.M and 5:30 P.M.
Find the difference.
8:15 A.M. 5:15 P.M ?H
5:30 PM 5:15 P.M ?M
Add the two difference
Step 2: Subtract 45 min from the time difference between 8:15 A.M. and 5:30 P.M.
8:15 A.M. 5:15 P.M 9H
5:30 PM 5:15 P.M 15M
9h 15min
9h 15min = 8h 75min
8h 75min – 45min = 8h 30min
Mona was correct. 8h 30min >7h
Plan
Read
Solve

25. a) The task must require students to make and test conjectures,
pose problems, look for patterns, and explore alternative
solution paths.
Problematic task.
Example
Find in the blanks with help of the following numbers to get the
maximum result.
2,3,4,5
5 2
× 4 3
2236
×
3. Worthwhile mathematical tasks

26. Example: Different ways of showing 2/5.
The task should be open-ended which foster
creative thinking and experimentation.
Problematic task.
40%
0.4

27. Practice Activity
Provide opportunities to practice what they are learning
Games can also be a means of developing fluency
and automaticity.
3. Worthwhile mathematical tasks

28. Multiplication Bingo

29. Multiplication Bingo
Resources: Button (Counter) of a different color, a copy of the game
Procedure
 The game is designed for two players, however, the Multiply Game can be played among two groups.
 All the multiple products which come in the table of 1 to 9 are placed in 6 X 6 table chart.
 A separate number sequence of 1 to 9 is placed at the end.
 Two counters are placed on the number sequence line, players can move any of the counters one by one.
 After each turn, numbers of both counters are multiplied and the player locates the product in the table chart with
his/her piece.
 The first who places 4 pieces in a row either in a vertical, horizontal or diagonal direction, wins the game.
File note: Students can play this game by using table books. After some time students will memorize the tables and will be
able to play this without the use of table books.
Handout 1:

30. 4. Making connections
Facilitate students in Making
connections between mathematics
topics, subjects, and everyday life
experiences.

31. 4. Making connections
1. Opportunities for making connections
For conceptual understanding, it is necessary to help students to make
connections between mathematical ideas.
For example:
In our schools, Fractions, decimals, percentage, and ratio are taught as a
separate topic, we must encourage students to see how these are linked
by exploring different representation.
For example, 2/5
40%
0.4

32. 4. Making connections
It helps students to develop conceptual understandings
and flexibility.
It is used to elicit students’ strategies.
It helps students to develop fluent and accurate
mathematical thinking.
2. Multiple solutions and representation

33. Base ten blocks
Example: 104-27
77

34. 1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
101 102 103 104 105 106 107 108 109 110
Number Chart
7
10
10
Example: 104-27

35. Place value
Example: 104-27
Hundred Ten Unit
10
100
10
10
10
10
10
10
10
10
10
11 1 1
11 1 1
1 1 1
10
10
10
10
10
10
10
1010
11 1 1
1 1 1
11 1
1 1 1
1 1 1
1

36. 1 0 4
- 2 7
10 19
7 7
Example: 104-27
Abstract

37. 4. Making connections
3. Connecting to everyday life
Students begin to view mathematics as relevant and
interesting by solving significant problems in their everyday
life.
Which statement is correct and why?
32
= 3 × 3
32
= 3 + 3
32
= 3 - 3

38. Length of a side of a square field is 250 m. What will be cost of levelling
the field at a rate of PKR-1000 per square meter?

39. 5. Mathematical
Communication
• Generate a classroom discussion that allows students to explain
and justify their solution.
• With teacher lead discussion, students learn ways to use
mathematical ideas, language, and methods.

40. 5. Mathematical
Communication
It involves,
• Highlighting students’ ideas.
• Helping students to develop their understanding
• Negotiating meaning with students
• To add an idea or take the discussion in another
direction

41. 6. Mathematical
Language
For example:
Times, multiply, out of, denominator,
less than, equal to, half
• Teachers should use and encourage specialized mathematical language
throughout the lesson/classroom discussions.
• It helps to grasp the meaning of a concept through the use of words or
symbols.
≤, ≥, ≠
, %, ,
3
,

42. • Use carefully selected tools, and representations to develop students’
thinking.
• It helps to think through a problem or test an idea.
7.Tool and
Representations
Technological toolsManipulative tools

43. a) Exploring students’ reasoning and probing their understanding.
b) Teacher questioning
c) Feedback
d) Self and peer assessment
8. Assessment for
LearningIt helps to
Monitor learning progress
Diagnose learning issues
Determine their needs for further learning
Techniques

44. 9.Teacher Knowledge
Content Knowledge
• Know big idea
• Think of, model, and use examples and metaphors.
Technological Pedagogical Content Knowledge.
It is a theory that was developed to explain the set of knowledge
that teachers need to teach their students a subject, teach
effectively, and use technology.