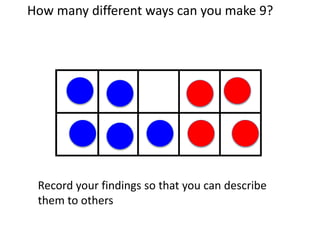
This document provides guidance for teachers on facilitating student problem solving and reasoning in mathematics through key teacher actions. It discusses posing challenging tasks, being clear about learning goals, and orchestrating mathematical discussions. Some important points are: teachers should select tasks that cannot be solved easily to encourage higher-level thinking; setting clear learning goals helps guide instruction; and facilitating productive class discussions involves techniques like revoicing students' reasoning and using wait time. The overall message is that teachers should aim to create an environment where students can grapple with open-ended problems and learn from each other through collaboration and explanation of their mathematical thinking.

1. Teaching maths through problem
solving: Facilitating student
reasoning
Louise Hodgson 2016

2. Learning intention
• For participants to become aware of key
teacher actions that promote student problem
solving and reasoning.

3. From the Australian National Numeracy
Review Report May 2008
From the earliest years, greater
emphasis be given to providing students
with frequent exposure to higher-level
mathematical problems…in contexts
of relevance to them, with increased
opportunities for students to discuss
…and explain their thinking.

4. From Impactful practices (from NCTM)
• Imagine classrooms where [children] are
working collaboratively, as well as
independently, using a range of resources.
• Imagine classrooms where the interactions
among students and with their teacher, are
focused on making sense of the mathematics…
• These are thinking and reasoning classrooms.

5. Guided by key teacher actions
1. Being clear about the purpose of
the lesson.
2. Posing challenging mathematical
tasks
3. Orchestrating mathematical
discussions

6. Key teacher action 1
Be clear about your purpose
‘Without explicit learning goals, it is difficult to
know what counts as evidence of students learning,
how students learning can be linked to particular
instructional activities and how to revise instruction
to facilitate students’ learning more effectively’.
‘Forming clear explicit learning goals sets the stage
for everything else’.
(Smith & Stein, 2011, p. 14)

7. In the Australian curriculum V8.0
The proficiency strands: reasoning,
problem-solving, understanding
and fluency describe how the
content is explored.

8. From the Australian Curriculum:
Mathematics
Students are reasoning mathematically when
they:
• explain their thinking,
• justify strategies used and conclusions
reached,
• adapt the known to the unknown
• prove that something is true or false
• compare and contrast related ideas and
explain their choices.

9. What might teachers do
to facilitate student
reasoning?
Turn and Talk with a
neighbour

10. What might teachers do to facilitate
student reasoning?
• Encourage students to solve problems in more
than one way
• Allow students to develop their own
approaches
• Encourage collaboration between students
• Use students’ explanations as the prompt to
explaining the mathematical intent of the task
and lesson.
Fraivillig (2004)

11. Children are more likely to reason if they
have developed a strategy for themselves
than if they are performing a procedure
they have been taught.
Such thinking for themselves takes time.
It comes only when children are working
on tasks that they do not know how to
solve.
(Sullivan & Davidson, 2014)

12. What is problem solving?
For a question to be a problem,
it must present a challenge
that cannot be resolved easily.
Problem solving is a process of
accepting a challenge and
striving to resolve it.’
(Polya, 1962)

13. Problem solving
• ‘Solving problems is a practical
art like swimming, or skiing, or
playing the piano:... if you wish to
learn swimming you have to go
into the water, and if you wish to
become a problem solver you
have to solve problems.’ (Polya 1962)

14. Problem Solving
In mathematics education, problem solving
has been emphasised since Polya’s work
in the 1940s.
1. Understand the problem
2. Devise a plan
3. Carry out the plan, and
4. Look back.

15. Quotes from PISA in Focus 37
• Teachers’ use of cognitive-activation
strategies, such as giving children
problems that require them to think
for an extended time, presenting
problems for which there is no
immediately obvious way of arriving
at a solution, and helping students to
learn from their mistakes, is
associated with students’ drive.

16. What implications does
this have for your
teaching?
What questions do you
have?
Turn and Talk with a
neighbour

17. Key teacher action 2
Select Challenging tasks
• Tasks that are cognitively challenging provide the
“grist” for worthwhile discussions. (Smith & Stein, 2011)
• Children need opportunities to grapple with a task for
which the solution method is not known in advance.
NCTM 2000
• Productive discussions that highlight key mathematical
ideas are unlikely to occur if the task on which students
are working requires limited thinking and reasoning.
(Smith & Stein, 2011)

18. WHY CHALLENGING TASKS ARE
IMPORTANT?

19. Comparing Two Mathematical Tasks
Patterns in the hundreds
square
Patterns on the hundreds
chart
Grade 1: Recognise, model, read, write and order numbers to at least
100. Locate these numbers on a number line (ACMNA013)

20. Patterns in the hundreds square

21. Patterns on the hundreds chart

22. Comparing two mathematical
tasks
1. Think privately
about the purpose
of each task.
2. Talk with your elbow
partner about how
they are the same
and how they are
different.

23. Comparing two mathematical
tasks
How are patterns in
the hundreds square
and the patterns on
the hundreds chart
the same and how
are they different?

24. Comparing Two Mathematical Tasks
Put 9 counters on a ten
frame
How many ways can you
make 9?
AC:M Foundation: Connect number names, numerals and quantities,
including zero, initially up to 10 and then beyond (ACMNA002)

25. Comparing two mathematical
tasks
1. Think privately
about the purpose
of each task.
2. Talk with your elbow
partner about how
they are the same
and how they are
different.

26. How many different ways can you make 9?
Record your findings so that you can describe
them to others

28. Enabling prompt(s) (for students
experiencing difficulty):
• Can be posed to students who have not been
able to make progress on the learning task.
Enabling prompts can involve slightly varying
an aspect of the task demand, such as:
– the form of representation,
– the size of the numbers, or
– the number of steps
(Sullivan, Zevenbergen, & Mousley, 2006)

29. Extending prompt (for those who
finish quickly):
• Some students might finish the learning task
quickly. The intention is such students be
posed “extending prompts” that extend their
thinking on an aspect of the learning task.
(Sullivan, Zevenbergen, & Mousley, 2006)

30. Mathematical tasks: A critical
Starting point for instruction
Not all tasks are created equal and
different tasks will provoke different
levels and kinds of thinking.
(Stein, Smith, Henningsen, & Silver, 2000)

31. Mathematical tasks
• If we want students to develop the capacity to
think, reason, and problem solve then we
need to start with high-level, cognitively
complex tasks.

32. In this approach
• Children are encouraged to find solutions to
problems by thinking for themselves before
instruction from the teacher.
• This is “fundamental to opportunities for
problem solving and reasoning” (Sullivan et al. 2015, p.
108)

33. Key teacher action 3
Orchestrate mathematical discussions
1. Anticipate
2. Monitor
3. Select
4. Sequence
5. Connect
Smith & Stein, 2011

34. Specific teacher moves to guide
discussion
• Using wait time
• Revoicing
• Asking students to state someone else’s
reasoning
• Asking students to apply their own reasoning
to someone else’s reasoning
• Prompting students for further participation

35. Teach children how to participate in a
discussion
 Idea: Sentence starters cue students to know
what to say
Explain to me what you meant by....
How is your way different from…
 This also helps students to learn what to listen
for so they can contribute to the discussion.
 Reinforcing norms support student persistence
and participation
(Kazemi and Hintz, 2014)

36. Norms…
• show how you get your
answers
• keep trying even if it is difficult
(it is meant to be)
• explain your thinking
• listen to other students

37. FINDING THE DIFFERENCE
BETWEEN TWO NUMBERS
A Sample grade 2 lesson

38. From the Australian Curriculum
This lesson addresses the following descriptor from AC
for year 2
• Group, partition and rearrange collections up to 1000
in hundreds, tens and ones to facilitate more
efficient counting (ACMNA028)
• Explore the connection between addition and
subtraction (ACMNA029)
• Solve simple addition and subtraction problems
using a range of efficient mental and written
strategies (ACMNA030)
There is also potential for students to come to Understand
number relationships, to be more Fluent with the mental
calculations, to find an efficient solution by Problem Solving, and
to develop Reasoning by explaining their strategy.

39. A sample grade 2 lesson
• Rationale for the lesson:
• Mental computation often involves strategies
to make the process easier. The focus in this
lesson is on different strategies for
partitioning (breaking a number into
convenient parts) and bridging (making up to
convenient numbers like 10, 100, etc) to solve
number problems mentally.

40. Explain goals for lesson
We are learning that here are many ways to find
the difference between two numbers

41. In this lesson, I need you to
• show how you get your answers
• keep trying even if it is difficult (it is meant to
be)
• explain your thinking
• listen to other students

42. The Zone of Confusion
• A space where students can be
encouraged to enter for powerful
problem solving processes to
occur

43. My friend Sophie is 18
years old. Her sister
Georgia is 25. How much
older is Georgia?
Introductory task/s

44. How Many more?
At the speedway the Ford car did 89
kilometres per hour (kph). The Holden car
did 111 kilometres per hour (kph). How
much faster was the Holden travelling.
Explain two different ways you could work
this out in your head.

45. If you are stuck
• The Ford car did 25 kph. The Holden car did 18
kph. How much faster was the ford car?
• The Ford car did 11 kph. The Holden car did 8
kph. How much faster was the ford car?

46. If you are stuck
• The Ford car did 11 kph. The Holden car did 8
kph. How much faster was the ford car?

47. If you have finished
• The Ford travelled 1035 kilometres. The
Holden travelled 989 kilometers. How
many more kilometers does the Holden
need to travel to catch up to the Ford?
• Explain how you can work it out in your
head.

48. The zone of confusion

49. Some final words…
• Posing challenging tasks requires a different lesson
structure
• Lessons should foster the sense of a classroom
community to which all children contribute with the
intention that children learn from each other
• The experience of engaging with the task happens
before instruction
• Few rather than many tasks
• All children are given time to engage sufficiently to
participate in the lesson summary.
(Sullivan and Davidson), 2014

50. What implications does
this have for your
teaching?
What questions do you
have?
Turn and Talk with a
neighbour

51. References
• Elham K., & Hintz, A. (2014). How to structure and lead productive Mathematical
Discussions. USA. Stenhouse.
• Fraivillig, J. (2004). Strategies for advancing children’s mathematical thinking. Teaching
Children Mathematics, 7, 454-459.
• NCTM, (2000). The Teaching Principle. Retrieved from
http://www.nctm.org/standards/content.aspx?id=26808
• Pólya, G. (1962). The teaching of mathematics and the biogenetic law. The Scientist
Speculates, 352-356.
• Stein, M. K., Engle, R. A., Smith, M. S., & Hughes, E. K. (2008). Orchestrating productive
mathematical discussions: Five practices for helping teachers move beyond show and tell.
Mathematical Thinking and Learning, 10(4), 313-340.
• Stein, M. K., Smith, M. S., Henningsen, M. A., & Edward, A. Silver. 2000. Implementing
Standards-Based Mathematics Instruction: A Casebook for Professional Development.
• Smith, M., & Stein, M. K. (2011). Five practices for orchestrating productive mathematics
discussions. Reston V.A. NCTM
• Sullivan, P., Zevenbergen, R., & Mousley, J. (2006). Teacher actions to maximize mathematics
learning opportunities in heterogeneous classrooms. International Journal for Science and
Mathematics Teaching, 4, 117-143.
• Sullivan, P., & Davidson, A. (2014). The role of challenging mathematical tasks in creating
opportunities for student reasoning. In J. Anderson, M. Cavanagh & A. Prescott (Eds.).
Curriculum in focus: Research guided practice (Proceedings of the 37th annual conference of
the Mathematics Education Research Group of Australasia).(pp. 605 – 612). Sydney.
• Sullivan, P., Walker, N., Borcek, C., Rennie, M. (2015). Exploring a structure for mathematics
lessons that foster problem solving and reasoning. In M. Marshman, V. Geiger & A. Bennison
(Eds.), Mathematics Education in the Margins: Proceedings of the 38th annual conference of
the Mathematics Education Research Group of Australasia. (pp. 41 -57). Sunshine Coast.