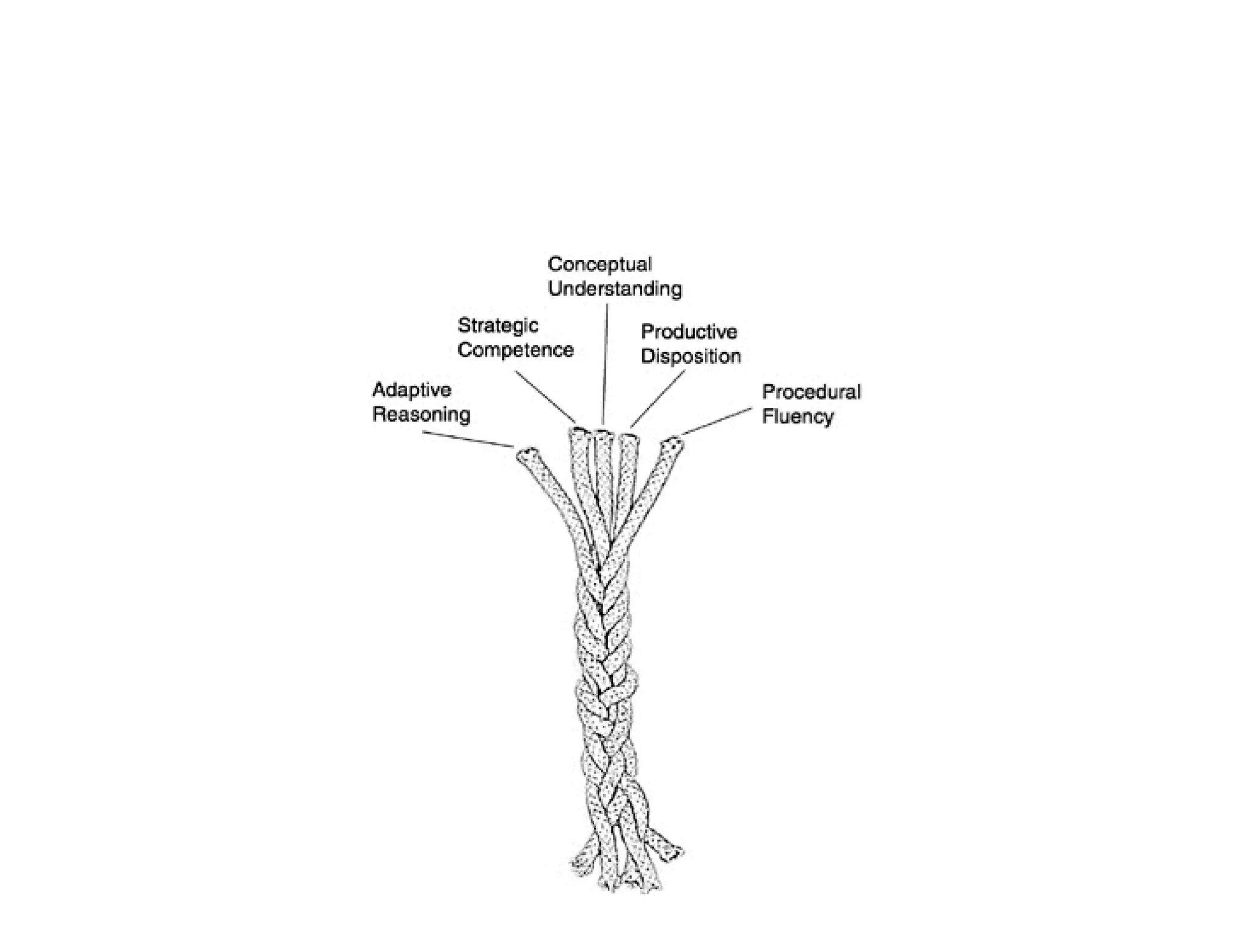
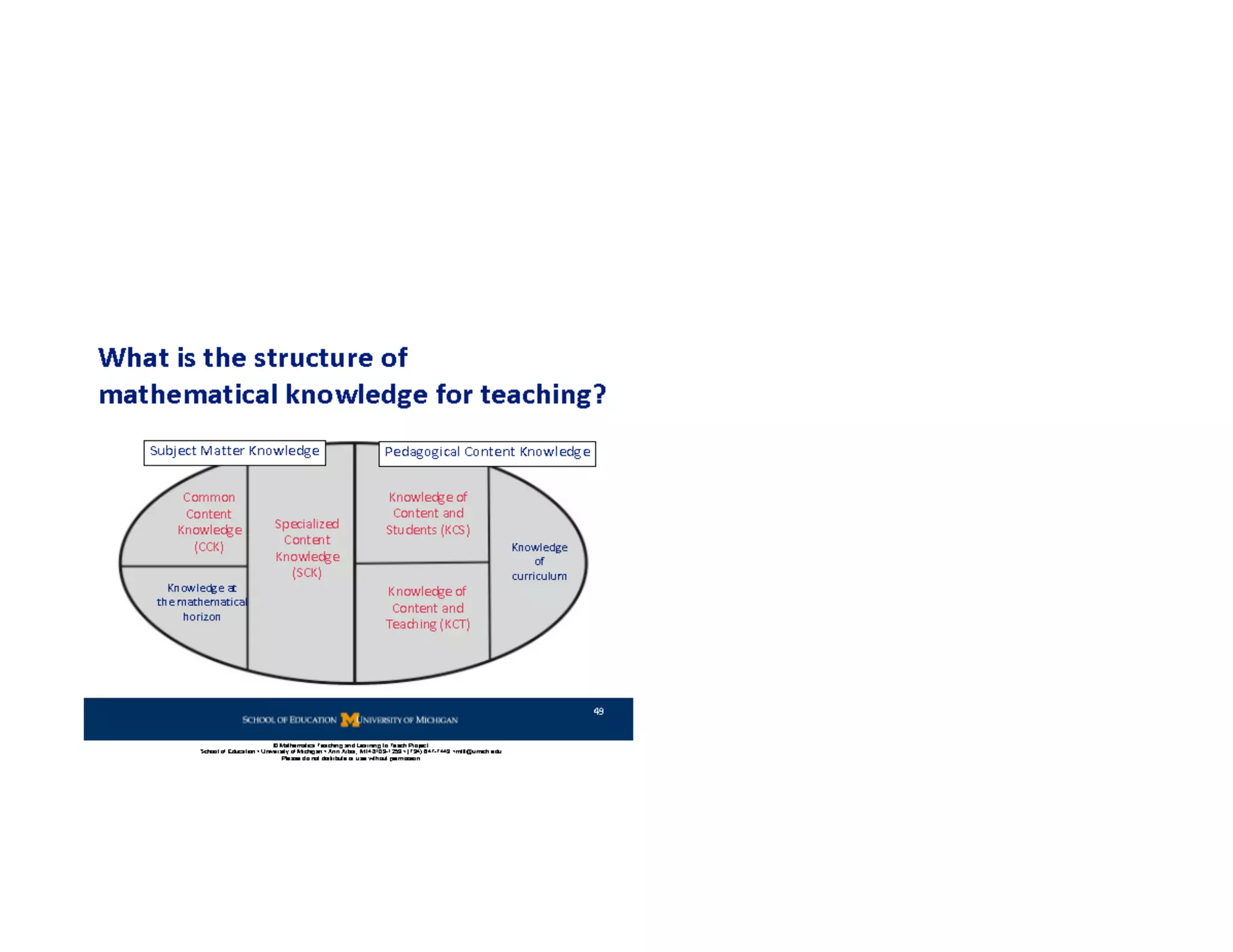
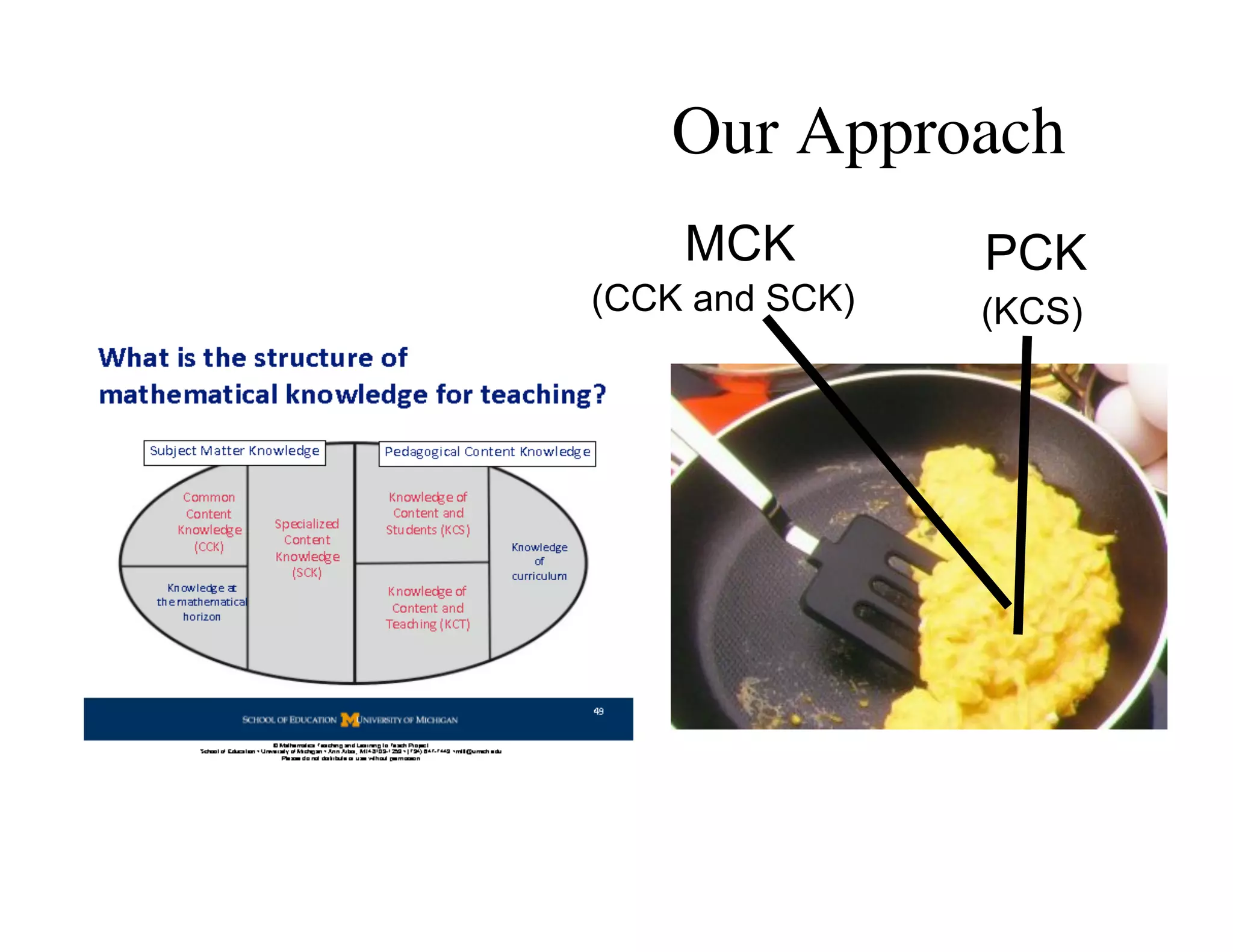
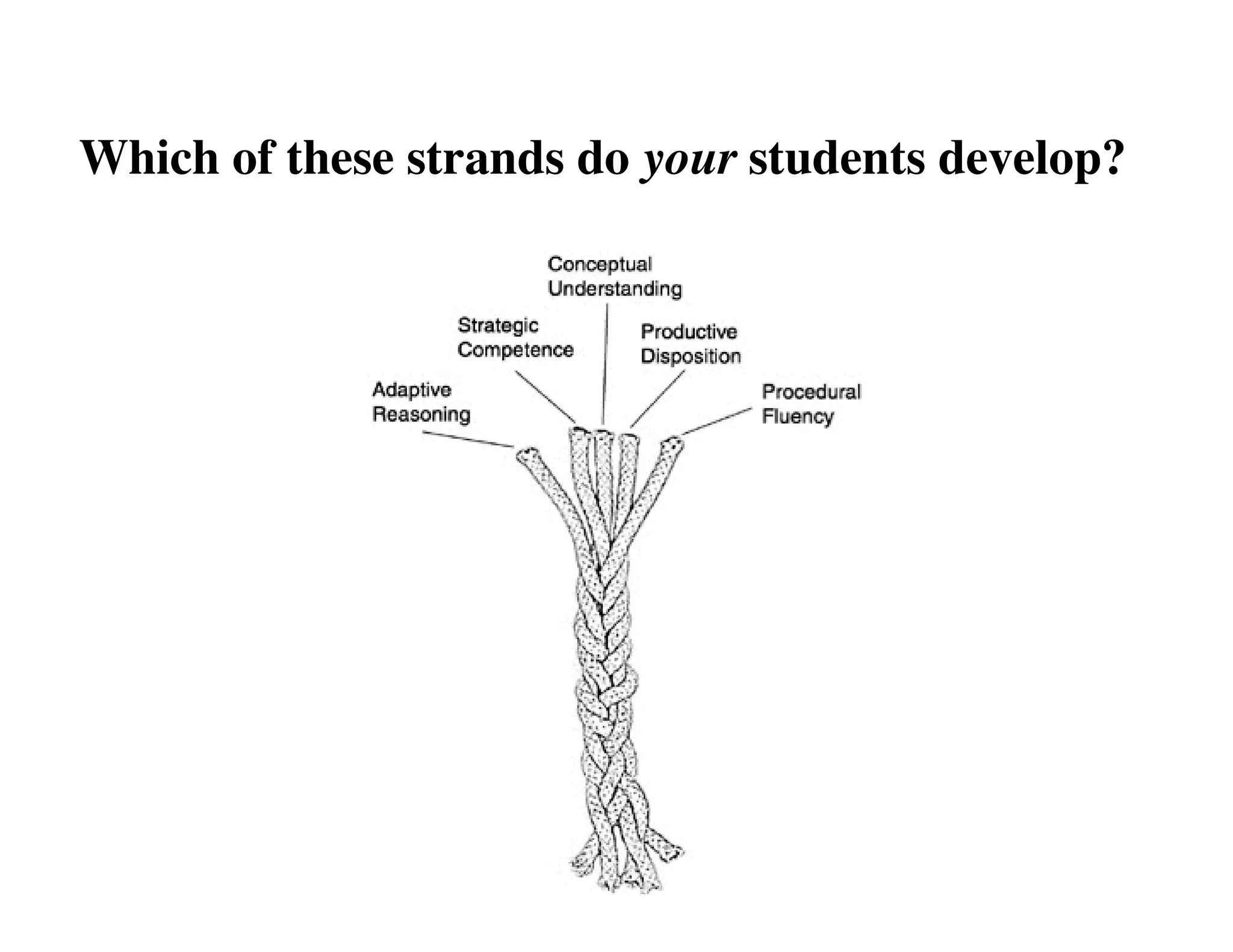
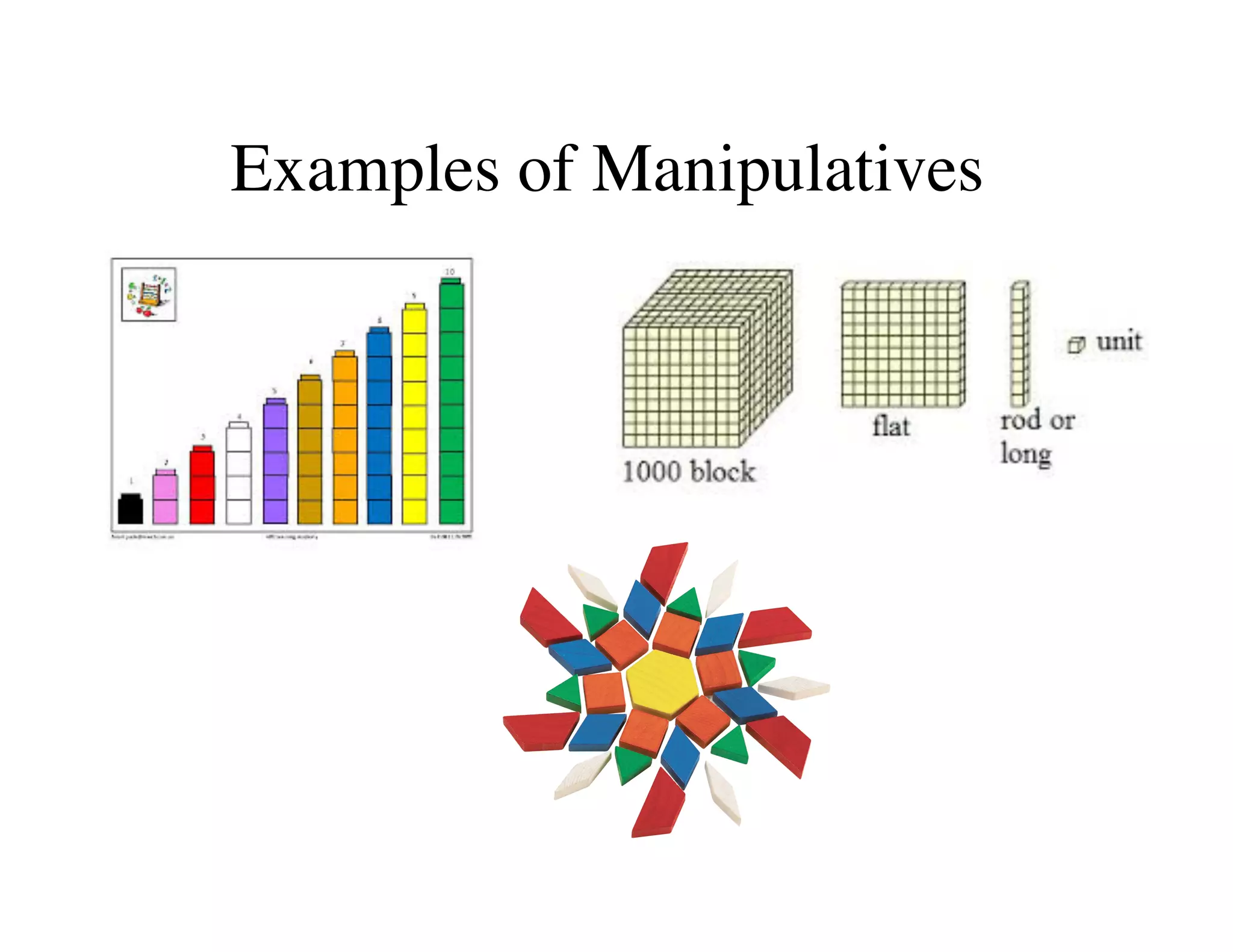
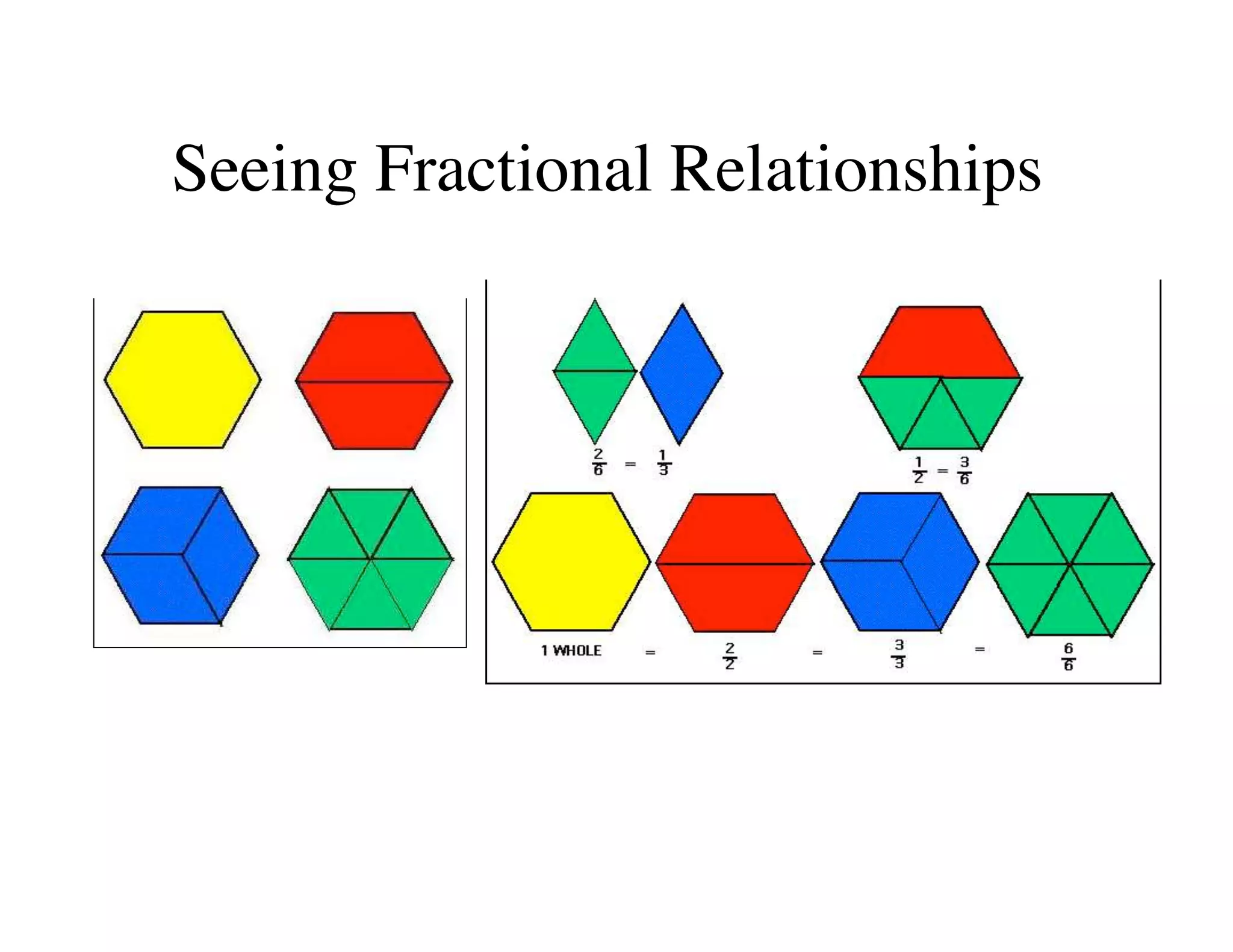
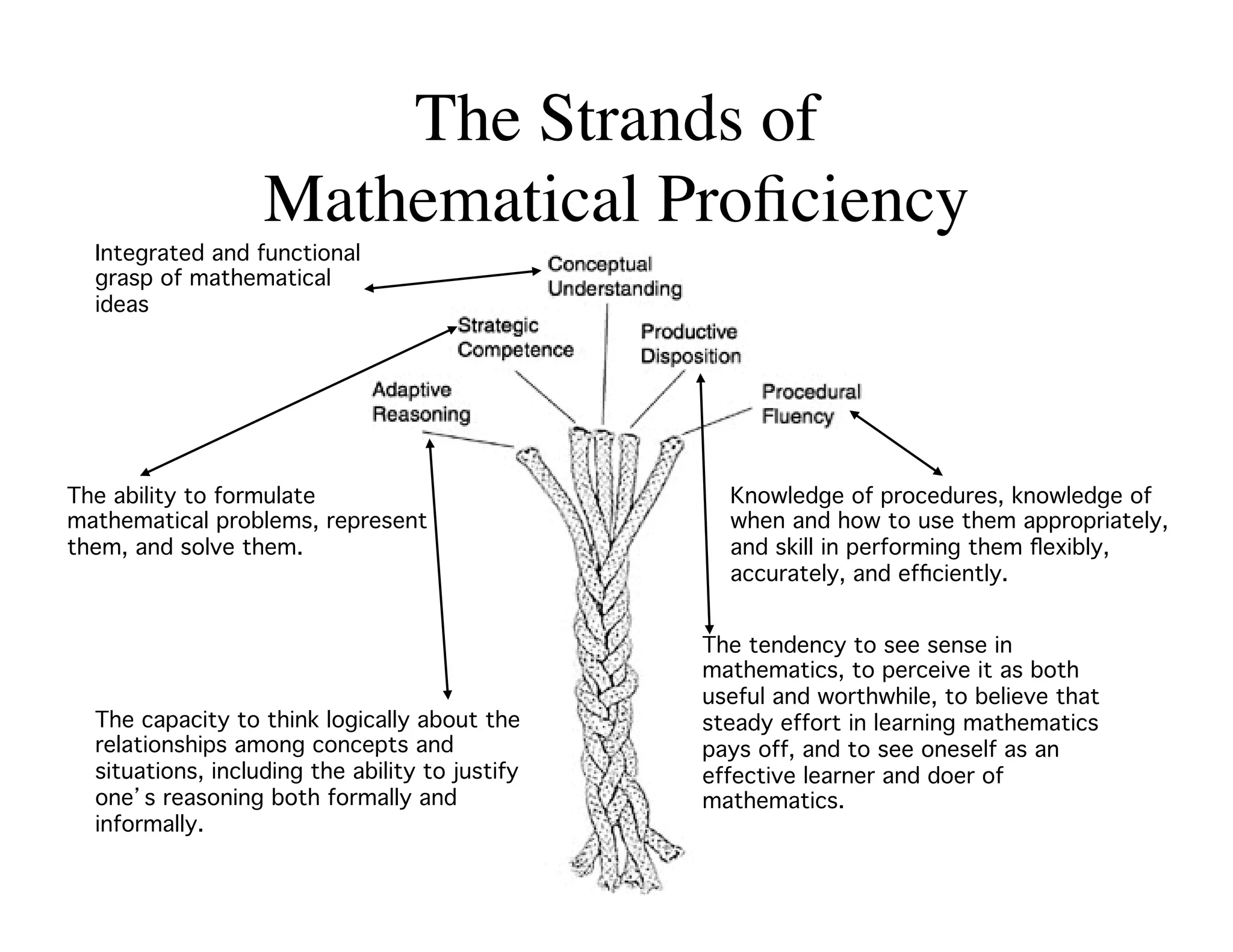
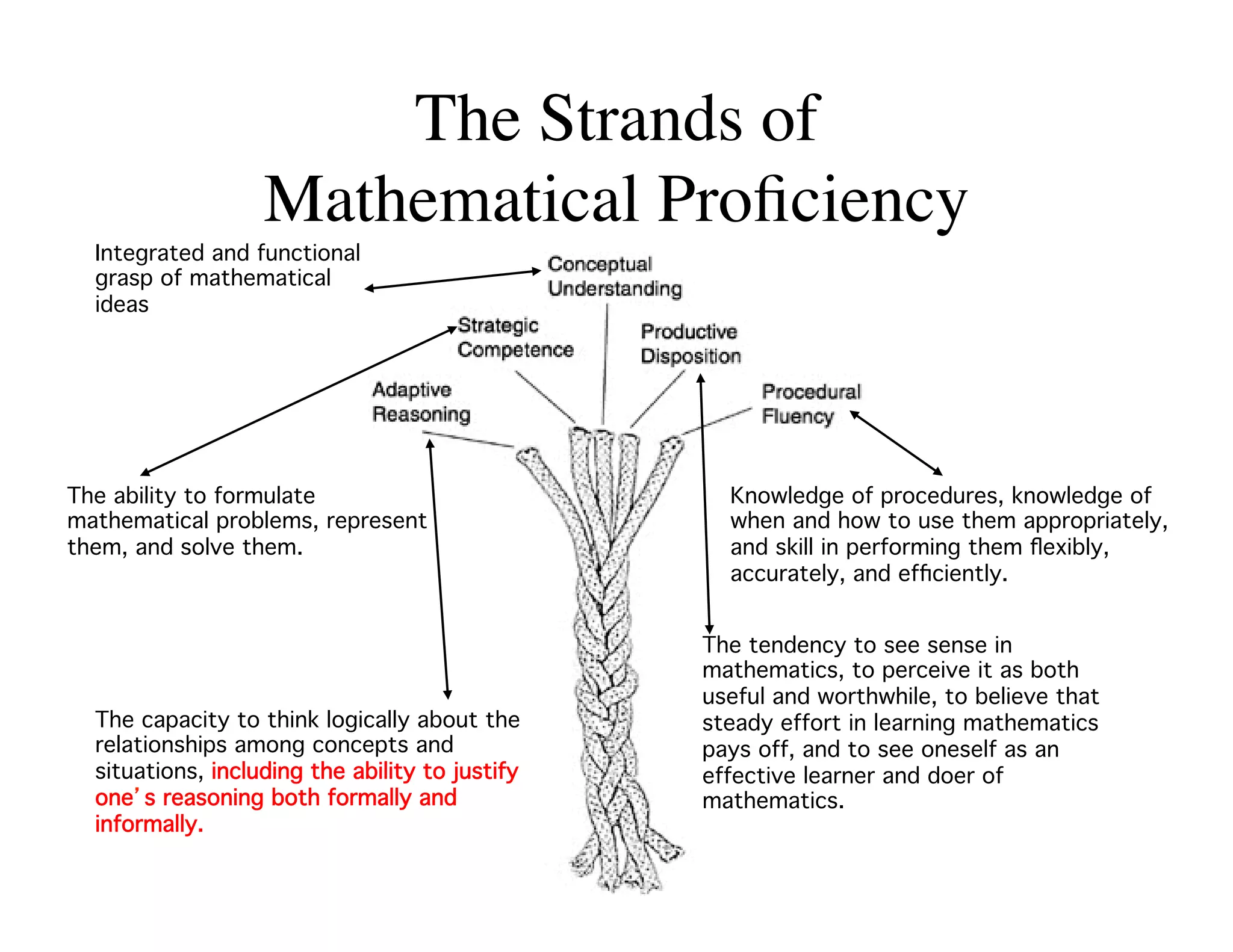
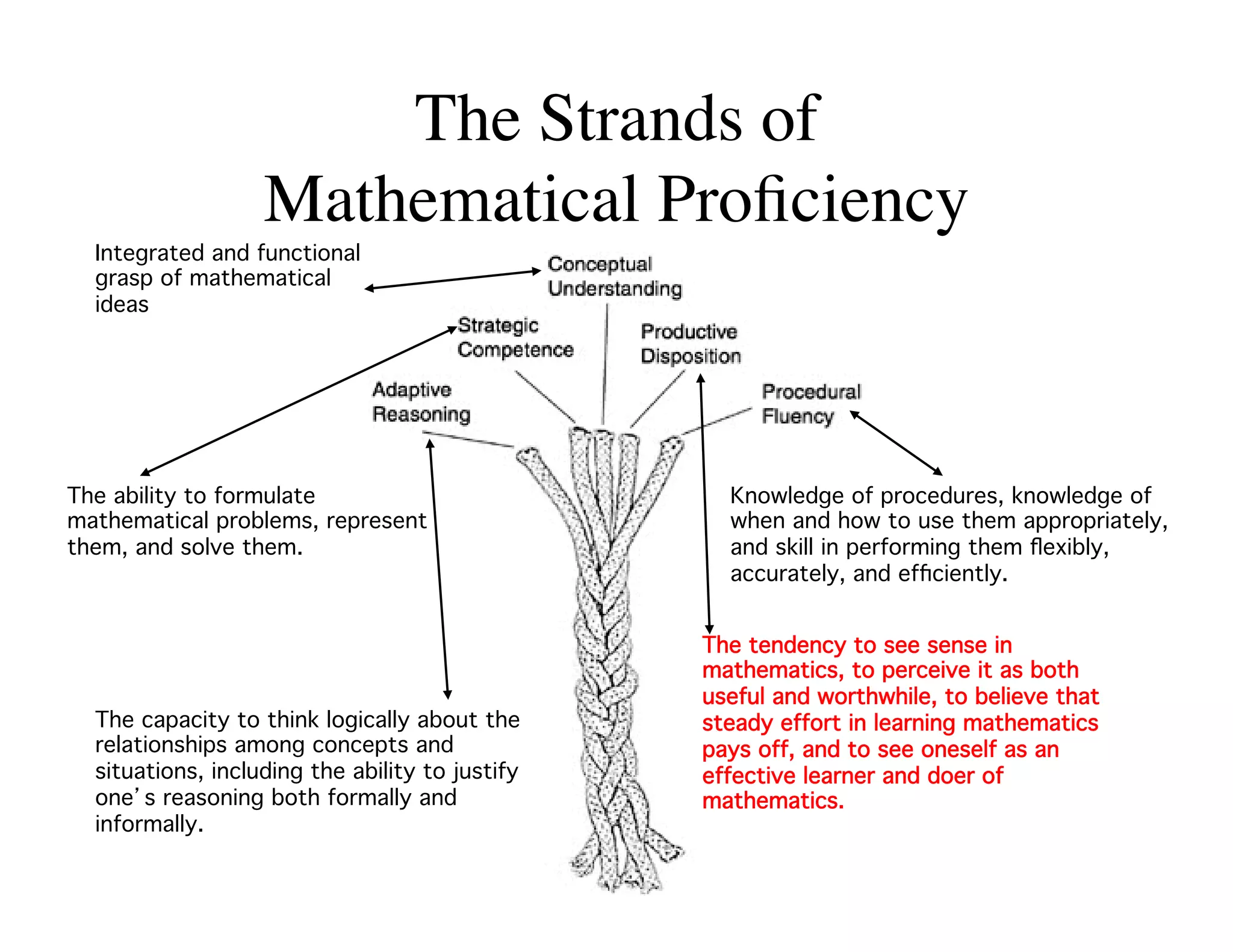
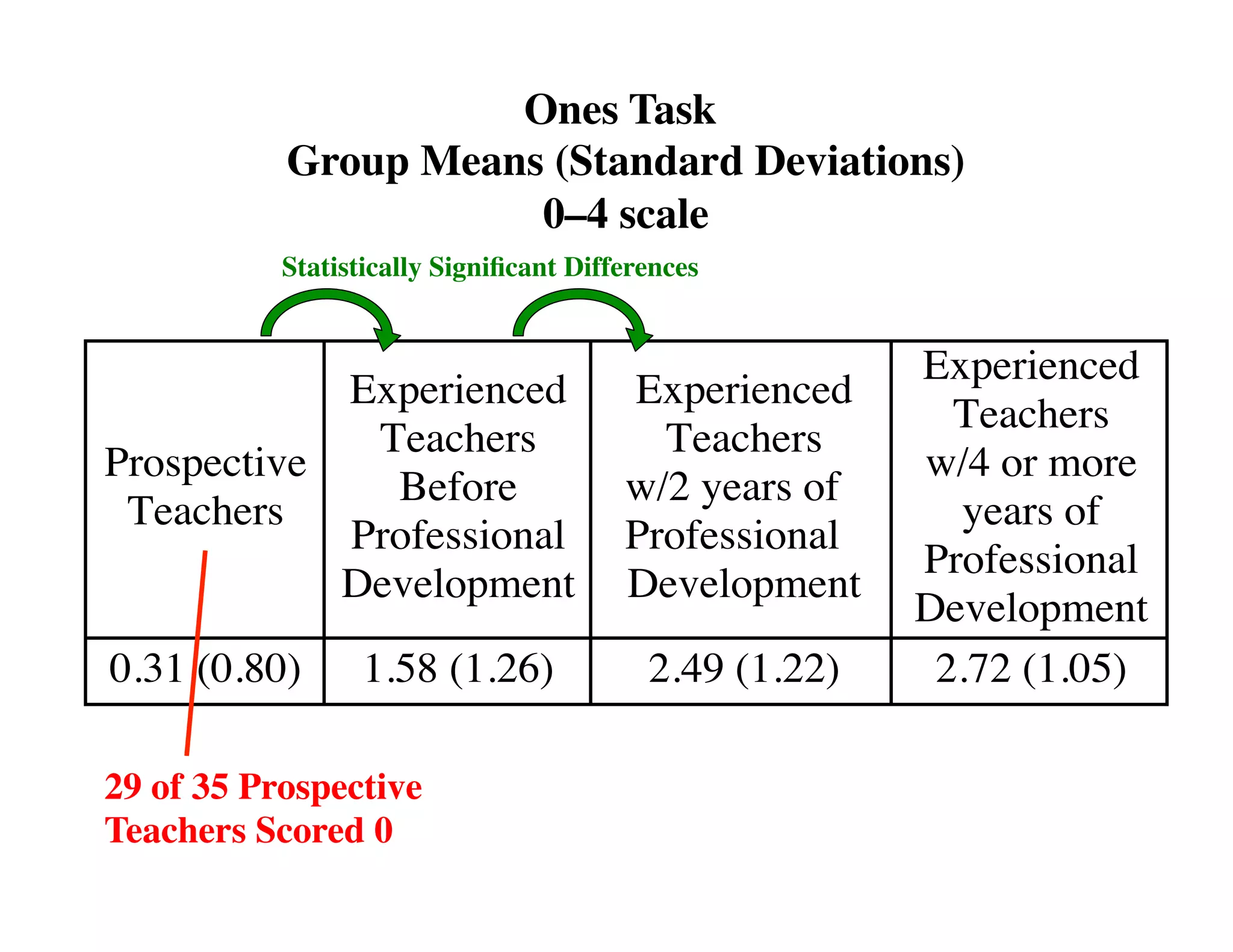
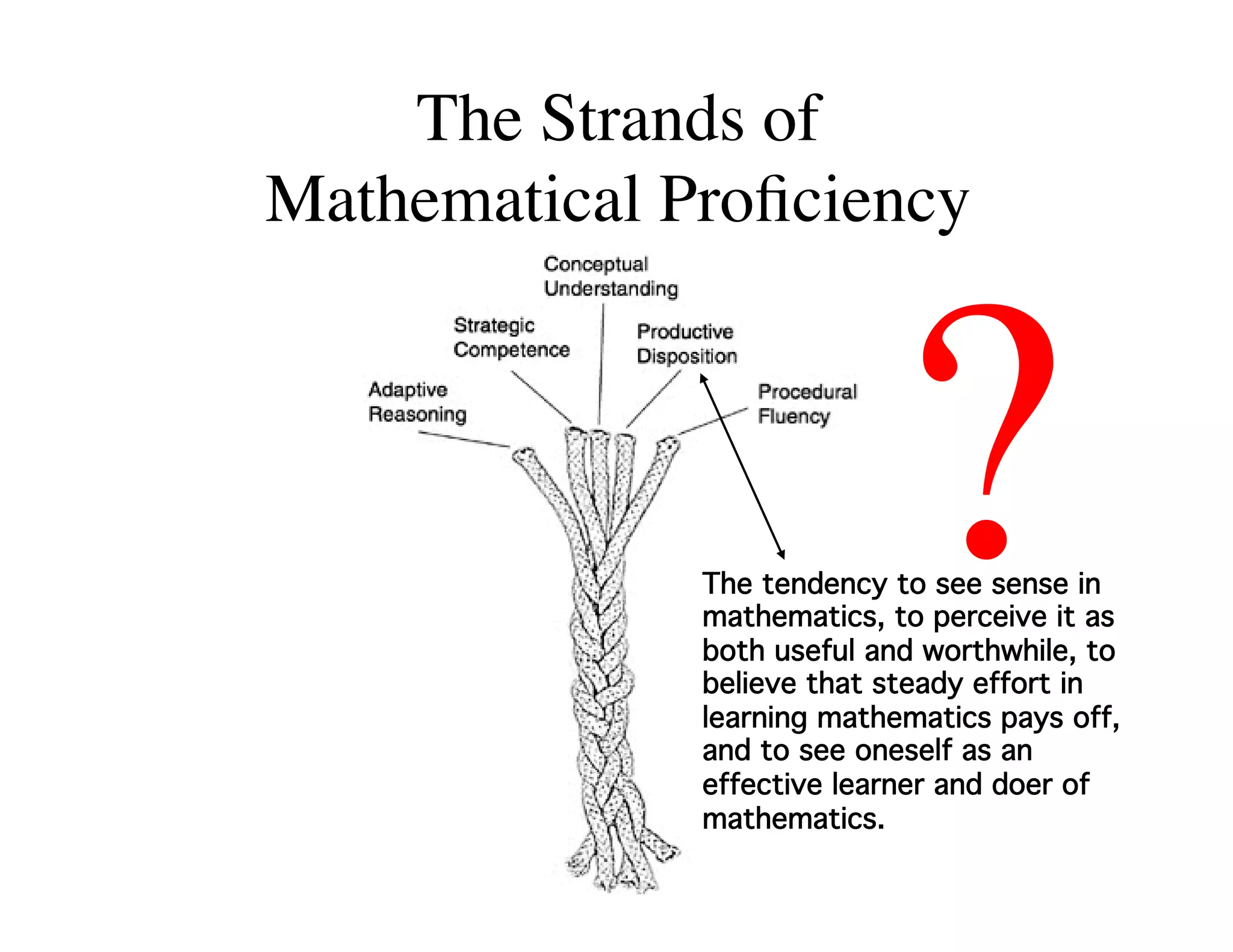
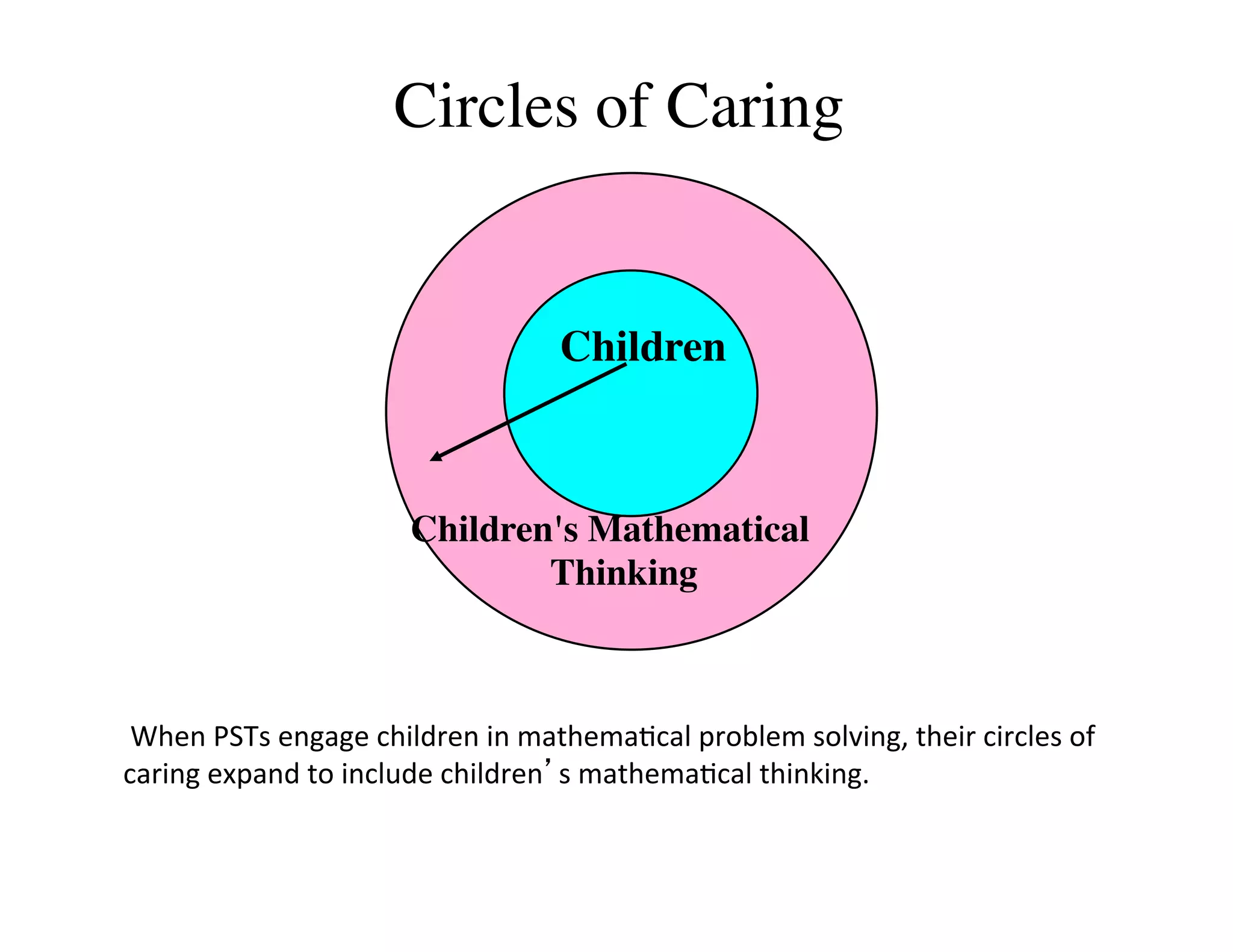
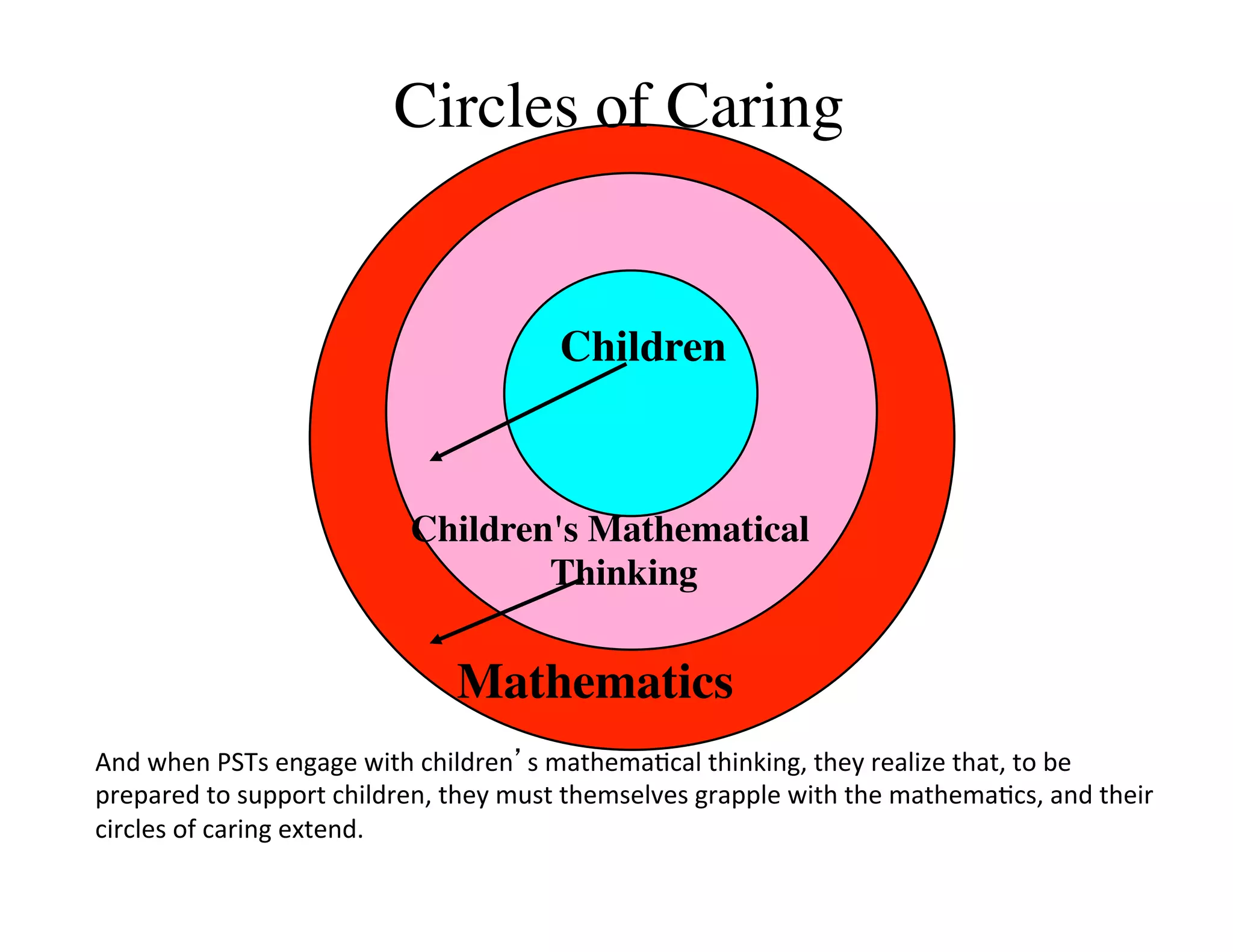
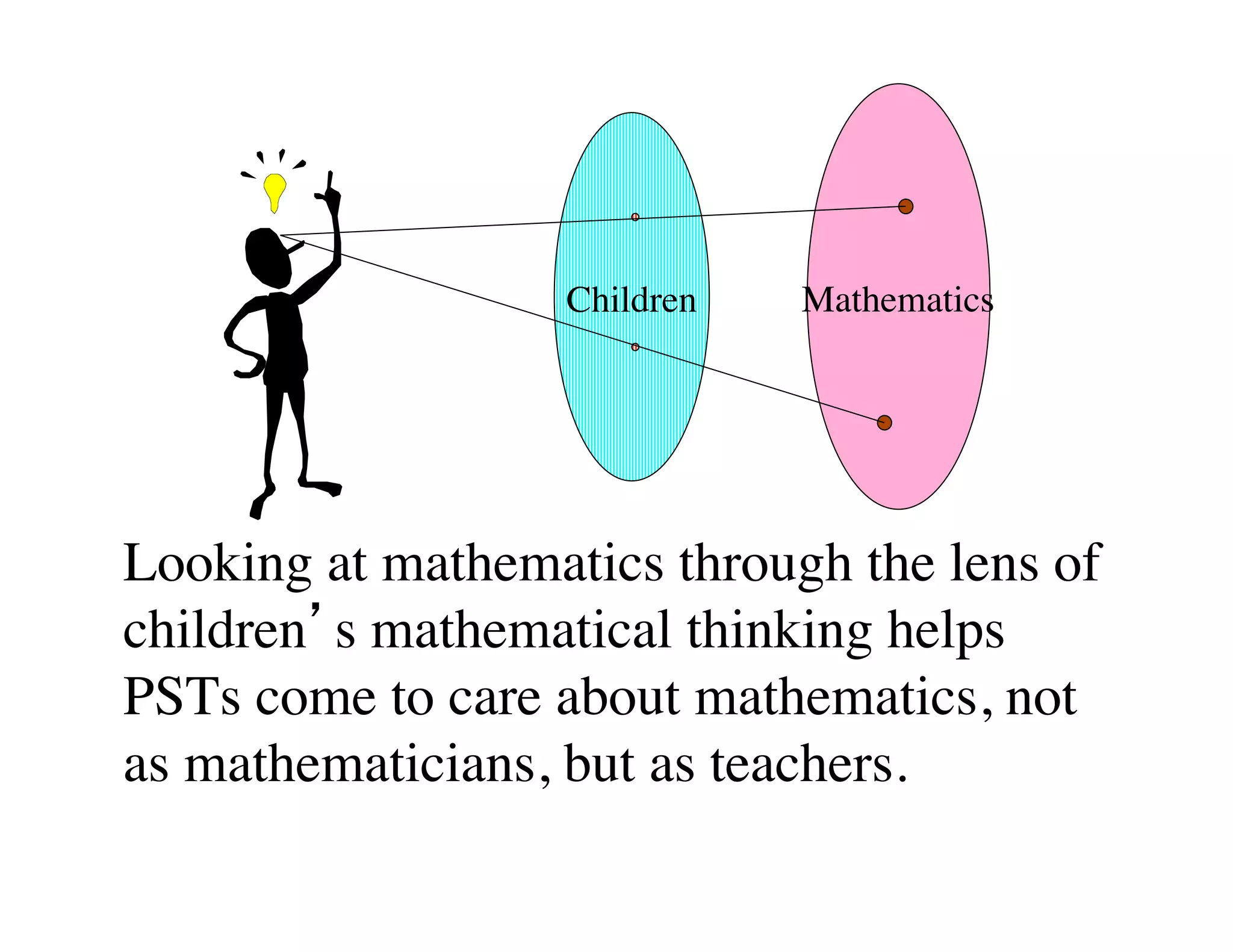
This document summarizes a presentation about preparing elementary school teachers to understand elementary mathematics. It discusses how elementary mathematics concepts can be complex and how focusing on children's mathematical thinking can help prospective teachers (PSTs) engage more deeply with mathematics. The presentation addresses four principles: 1) How students typically learn mathematics is problematic, 2) Learning concepts is more powerful than procedures, 3) Students' reasoning is varied and complex, and 4) Elementary math is not as elementary as assumed. Research found PSTs who learned about children's thinking improved their math knowledge and developed more sophisticated beliefs than those who did not.

















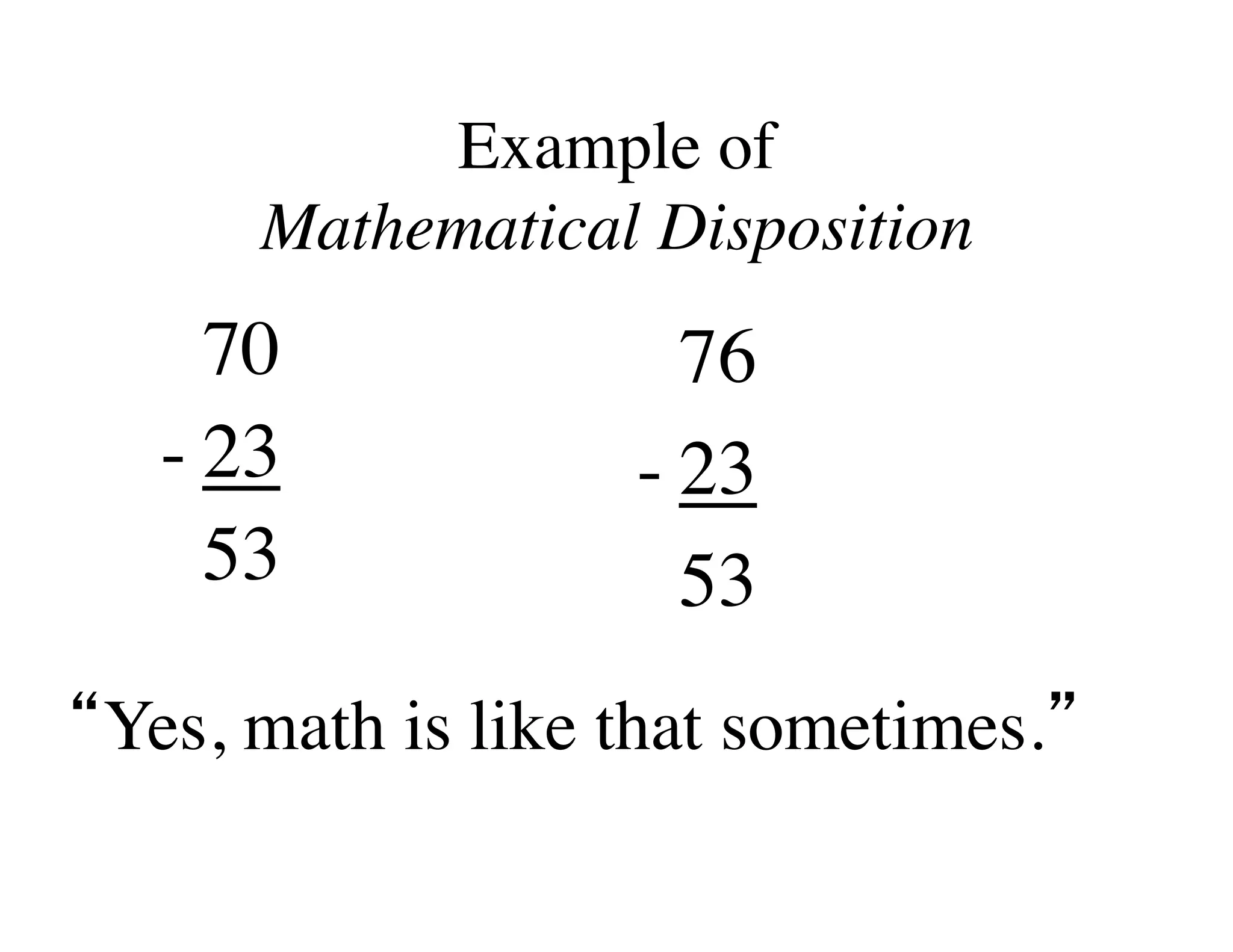







![This
idea
is
at
least
100
years
old.
John Dewey, 1902
Every
subject
has
two
aspects,
“one
for
the
scien=st
as
a
scien=st;
the
other
for
the
teacher
as
a
teacher”
(p.
351).
“[The
teacher]
is
concerned,
not
with
the
subject-‐maFer
as
such,
but
with
the
subject-‐maFer
as
a
related
factor
in
a
total
and
growing
experience
[of
the
child]”
(p.
352).
!
!
Dewey, J. (1902/1990). The child and the curriculum.
Chicago: The University of Chicago Press. !](https://image.slidesharecdn.com/qwc5hktcgvdpwp1guzyw-signature-ad95e2248ce0b328f93e90463efa1e299db3423ce6a37df2f25301dada4a2fc7-poli-140924075046-phpapp01/75/Philipp-pm-slides-39-2048.jpg)




















![Javier*, Grade 5
How many eggs are in six cartons (of one dozen)?
Javier thinks for 15 seconds, and says, “72.”
I: How did you get that?
Javier writes and says, “5 times 12 is 60, and 12
more is 72.”
I: “How did you know 12 x 5 is 60?”
J: “Because 12 times 10 equals 120. If I take
the [sic] half of 120, that would be 60.”
*At the time of this interview, Javier had been in the United States about one year, and
he did not speak English before coming to this country.](https://image.slidesharecdn.com/qwc5hktcgvdpwp1guzyw-signature-ad95e2248ce0b328f93e90463efa1e299db3423ce6a37df2f25301dada4a2fc7-poli-140924075046-phpapp01/75/Philipp-pm-slides-61-2048.jpg)
![One Representation of Javier’s Thinking
6 x 12
= (5 x 12) + (1 x 12)
= [(1
2
x 10) x 12] + 12
= [1
2
x (10 x 12)] + 12
= [1
2
x (120)] + 12
= 60 + 12
= 72
(Distributive prop. of x over +)
(Substitution property)
(Associative property of x)
Place value
What would a teacher need to know to
understand Javier’s thinking, and where do
teachers learn this?](https://image.slidesharecdn.com/qwc5hktcgvdpwp1guzyw-signature-ad95e2248ce0b328f93e90463efa1e299db3423ce6a37df2f25301dada4a2fc7-poli-140924075046-phpapp01/75/Philipp-pm-slides-62-2048.jpg)