Teks tersebut merupakan ringkasan tentang distribusi Poisson. Distribusi Poisson adalah distribusi probabilitas untuk variabel acak diskret yang menentukan jumlah kejadian yang terjadi dalam interval waktu tertentu. Rumus distribusi Poisson menghitung probabilitas dengan asumsi kemungkinan sukses sangat kecil dan jumlah percobaan sangat besar. Teks tersebut juga menjelaskan ciri-ciri dan contoh penerapan distribusi Poisson.

1. StatistikaProbabilitasDiskrit Poisson| STMIK PROVISI 2013
DISTRIBUSI POISSON
Farkhan Rauf Hafiidh
Program Studi Teknik Informatika , STMIK ProVisi Semarang
Email : Farkhan.erha@yahoo.com
Abstrak – penentuan nilai dengan probabilitas saat ini mulai marak digunakan ,dengan adanya distribusi poisson,
mempermudah untukmengetahui probabilitas sebuah cara perhitungan yang dinilai cukup sulit untuk diketahui nilai pada
akhir perhitungan.
Keywords: Probabilitas ; Poisson
I. PENDAHULUAN
Himpunan pasangan nilai-nilai variable acak X dengan
probabilitas nilai-nilai variable acak X, P(X = x) disebut
probabilitas X atau disingkat distribusi X. Distribusi diskrit
memiliki nilai variable acak X yangbernilai diskrit pada
suatu waktu. Ada beberapa jenis distribusi diskrit yang biasa
digunakan yaitu distribusi seragam diskrit (uniform
distribution), Binomial, Hipergeometrik, Distribusi Binomial
Negatif dan Geometrik, dan Poisson Distribusi poisson
disebut juga distribusi peristiwa yang jarang terjadi,
ditemukan oleh S.D. Poisson (1781–1841), seorang ahli
matematika berkebangsaan Perancis. Distribusi Poisson
termasuk distribusi teoritis yang memakai variabel random
diskrit.Menurut Walpole (1995), distribusi poisson adalah
distribusi peluang acak poisson X, yang menyatakan
banyaknya sukses yang terjadi dalam suatu selang waktu
atau daerah tertentu.
II. PengertianDistribusi Poisson
Distribusi poisson adalah Percobaan-percobaan yang
menghasilkan nilai-nilai numeric suatu variable acak
X,jumlah keluaran yang terjadi selama suatu selang waktu
yang diketahui atau didalam suatu daerah(ruang) yang
ditentukan disebut sebagai percobaan Poisson.
III. Ciri – Ciri Distribusi Poisson
Hasil percobaan pada suatu selang waktu dan tempat
tidak tergantung dari hasil percobaan diselang waktu dan
tempat yang lain yang terpisah.
• Peluang terjadinya suatu hasil percobaan
sebanding dengan panjang selang waktu dan
luas tempat percobaan terjadi.Hal ini
berlakuhanya untuk selang waktu yang singkat
dan luas daerah yang sempit.
• Peluang lebih dari satu hasil percobaan akan
terjadi pada satu selang waktu yang singkat dan
luasan tempat yang sama diabaikan.

2. StatistikaProbabilitasDiskrit Poisson| STMIK PROVISI 2013
IV. Pembahasan
a. Sifat Distribusi Poisson
Jumlah keluaran yang terjadi didalam satu selang
waktu/daerah yang ditentukan tidak tergantung dari
jumlah yang terjadi didalam setiap selang
waktu/daerah ruang yang tak berhubungan lainnya.
Dapat disimpulkan bahwa proses Poisson tidak
memiliki memori
Probabilitas sebuah keluaran tunggal akan terjadi
selama suatu selang waktu yang singkat atau dalam
suatu daerah kecil sebanding dengan lama
waktu/ukuran daerah itu dan tidak bergantung pada
jumlah keluaran yang terjadi diluar selang waktu
atau daerah ini
Probabilitas bahwa lebih dari satu keluaran akan
terjadi didalam suatu selang waktu yang singkat atau
jatuh pada suatu daerah yang kecil semacam itu
dapat diabaikan
b. Proses Dari Distribusi Poisson
 Percobaan Bernoulli menghasilkan variable
random X yang bernilai numerik, yaitu
jumlah sukses yang terjadi.
 Jika pengamatan dilakukan pada suatu
rentang interval waktu, maka dapat diamati
bahwa variable random X adalah terjadinya
sukses selama waktu tertentu
 Jika perhatian ditujukan pada kejadian
sukses yang muncul(lahir) pada suatu
rentang yang kecil, maka terjadi sebuah
proses kelahiran(birth atau arrival process)
atau dikenal sebagai proses Poisson
c. Rumus Distribusi Poisson
Rumus Pendekatan Peluang Poisson untuk
Binomial
Pendekatan Peluang Poisson untuk Peluang
Binomial dilakukan untuk mendekatkan probabilitas
probabilitas dari kelas sukses (x) dari n percobaan
Binomial dalam situasi dimana n sangat besar dan
probabilitas kelas sukses (p) sangat kecil. Aturan
yang diikuti oleh kebanyakan ahli statistika adalah
bahwa n cukup besar dan p cukup kecil, jika n
adalah 20 atau lebih dari 20 dan p adalah 0.05 atau
kurang dari 0.05.
Rumus pendekatannya adalah :
P ( x ; μ ) = e – μ
. μ X
X !
Dimana : e = 2.71828
μ = rata – ratakeberhasilan = n . p
x = Banyaknya unsur berhasil dalam sampel
n = Jumlah / ukuran populasi
p = probabilitas kelas sukses

3. StatistikaProbabilitasDiskrit Poisson| STMIK PROVISI 2013
d. contoh Soal
Contoh 1.1
1.Dua ratus penumpang telah memesan tiket untuk
sebuah penerbangan luar negeri. Jika probabilitas
penumpang yang telah mempunyai tiket tidak akan
datang adalah 0.01 maka berapakah peluang ada 3 orang
yang tidak datang.
Jawab :
Dik : n = 200, P = 0.01, X = 3, μ = n . p = 200 . 0.01 = 2
P ( x ; μ ) = e – μ
. μX
X!
= 2.71828 – 2
. 2 3
= 0.1804
atau 18.04 %
3!
Contoh studi kasus.
1. Rata-rata seorang sekretaris baru melakukan 5
kesalahan ketik per halaman. Berapa peluang bahwa pada
halaman berikut ia membuat:
a. tidak ada kesalahan?
b. tidak lebih dari 3 kesalahan?
c. lebih dari 3 kesalahan?
d. paling tidak ada 3 kesalahan?
Jawab :
a. Peluang halaman tidak ada kesalahan (x = 0, = 5.0)
 P(0 ; 5.0) = 0.0067
b. Peluang halaman tidak lebih dari 3 kesalahan (x 3, =
5.0)
 P(x 3 ; 5.0) = P(0 ; 5.0) + P(1 ; 5.0) + P(2 ;5.0) +
P(3 ; 5.0)
 P(x 3 ; 5.0) = 0.0067 + 0.0337 + 0.0842 + 0.1404
 P(x 3 ; 5.0) = 0.2650
c. Peluang halaman lebih dari 3 kesalahan (x  3, = 5.0)
 P(x 3 ; 5.0) = P(4 ; 5.0) + P(5 ; 5.0) + P(6 ; 5.0) +
P(7 ; 5.0) + ...... + P(15 ; 5.0)
atau
 P(x > 3 ; 5.0) = 1 - P(x 3 ; 5.0)
 P(x > 3 ; 5.0) = 1 - [ P(0 ; 5.0) + P(1 ; 5.0) + P(2;
5.0) + P(3 ; 5.0) ]
 P(x > 3 ; 5.0) = 1 - [ 0.0067 + 0.0337 + 0.0842 +
0.1404 ]
 P(x > 3 ; 5.0) = 1 - 0.2650
 P(x > 3 ; 5.0) = 0.7350
d. Peluang halaman paling tidak ada 3 kesalahan (x  3,
= 5.0)
 P(x  3 ; 5.0) = P(3 ; 5.0) + P(4 ; 5.0) + P(5 ; 5.0) +
P(6 ; 5.0) + ...... + P(15 ; 5.0)
atau
 P(x  3 ; 5.0) = 1- P(x < 3 ; 5.0)
 P(x  3 ; 5.0) = 1 - [ P(0 ; 5.0) + P(1 ; 5.0) + P(2 ;
5.0) ]
 P(x  3 ; 5.0) = 1- [ 0.0067 + 0.0337 + 0.0842 ]
 P(x  3 ;5.0) = 1 - 0.1246
 P(x  3 ; 5.0) = 0.8754
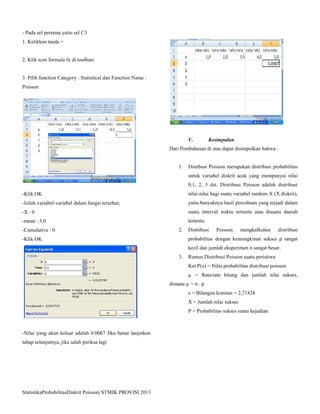
Menggunakan MS Excel Untuk Distribusi Poisson
-Buka program EXCEL
- Pada lembar kerjanya isikan data berikut :
- Supaya seragam nilai di-set dengan 4 angka di belakang
koma

4. StatistikaProbabilitasDiskrit Poisson| STMIK PROVISI 2013
- Pada sel pertama yaitu sel C3
1. Ketikkan tanda =
2. Klik icon formula fx di toolbars
3. Pilih function Category : Statistical dan Function Name :
Poisson
-Klik OK
-Isilah variabel-variabel dalam fungsi tersebut;
-X : 0
-mean : 5,0
-Cumulative : 0
-Klik OK
-Nilai yang akan keluar adalah 0.0067 Jika benar lanjutkan
tahap selanjutnya, jika salah periksa lagi
V. Kesimpulan
Dari Pembahasan di atas dapat disimpulkan bahwa :
1. Distibusi Poisson merupakan distribusi probabilitas
untuk variabel diskrit acak yang mempunyai nilai
0,1, 2, 3 dst. Distribusi Poisson adalah distribusi
nilai-nilai bagi suatu variabel random X (X diskrit),
yaitu banyaknya hasil percobaan yang terjadi dalam
suatu interval waktu tertentu atau disuatu daerah
tertentu.
2. Distribusi Poisson mengkalkulasi distribusi
probabilitas dengan kemungkinan sukses p sangat
kecil dan jumlah eksperimen n sangat besar.
3. Rumus Distribusi Poisson suatu peristiwa
Ket P(x) = Nilai probabilitas distribusi poisson
µ = Rata-rata hitung dan jumlah nilai sukses,
dimana µ = n . p
e = Bilangan konstan = 2,71828
X = Jumlah nilai sukses
P = Probabilitas sukses suatu kejadian