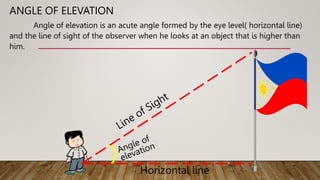
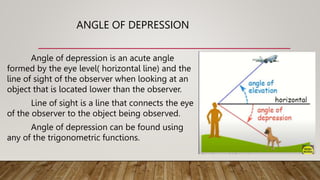
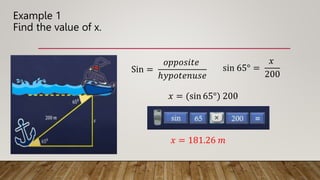
The document defines and provides examples of calculating angles of elevation and depression. It explains that angle of elevation is formed when looking at an object higher than the observer, while angle of depression is formed when looking at an object lower than the observer. Examples are provided to demonstrate calculating unknown lengths using trigonometric functions like tangent, sine and cosine based on the angles of elevation or depression and known lengths.

1. ANGLE OF ELEVATION AND
ANGLE OF DEPRESSION
• ILLUSTRATES ANGLES OF ELEVATION AND ANGLES OF
DEPRESSION.

2. Horizontal line
Angle of elevation is an acute angle formed by the eye level( horizontal line)
and the line of sight of the observer when he looks at an object that is higher than
him.
ANGLE OF ELEVATION

3. STEPS IN SOLVING MATH PROBLEMS INVOLVING
ANGLE OF ELEVATION
1. Draw an illustration that visualizes the problem and label it using the
given information.
2. Formulate a ratio of a given measure and the variable representing
what is being asked in the problem.
3. Form an equation using the formulated ratio and the trigonometric
function defined by the ratio.
4. Solve the solution of the equation and the solution of the problem.
5. Label your final answer correctly.

4. SOME REMINDERS IN DETERMINING THE
FUNCTION USE:
• If the measures of either leg and the hypotenuse of
the right triangle are given, then sine or cosine
function may be used.
• If the measures of the legs of the right triangle are
given , then tangent function is to be used.

5. Example 1
The A and R state building is 1, 200 m tall. What is the angle of
elevation of the top from the point on the ground 1, 750m from the
base of the building?
Let 𝜗 be the angle of elevation of the top from a point of the
ground.
tan =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 tan =
1200
1750
tan = 0.6857
𝑌𝑜𝑢 𝑎𝑟𝑒 𝑔𝑜𝑖𝑛𝑔 𝑡𝑜 𝑢𝑠𝑒 shift" if you are finding angle.

6. Example 2
A tower is 15.24 m high. At a certain distance away from a
tower, a man on the level ground observes that the angle of
elevation of the top of the tower is 41°. How far is the man from the
tower?
tan =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 tan 41° =
15.24
𝑥
tan 41° 𝑥 = 15.24
𝑥 =
15.24
tan 41°
𝑥 = 17.53 𝑚

7. Example 3
suppose that when the angle of elevation of the sun is 63.4°, a
building casts a shadow of 37.5 feet. How tall is the building?
tan =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
tan 63.4° =
𝑦
37.5 𝑦 = (tan 63.4°) 37.5
𝑦 = (tan 63.4°) 37.5
𝑦 = 74.89

8. DO IT ON YOUR OWN.
• A ladder leaning against a wall makes an angle of 80° with the ground.
If the foot of the ladder is 7 feet from the base of the wall , what is the
length of the ladder?
ℎ = 40.31
cos 80° =
7
ℎ

9. Angle of depression is an acute angle
formed by the eye level( horizontal line) and the
line of sight of the observer when looking at an
object that is located lower than the observer.
Line of sight is a line that connects the eye
of the observer to the object being observed.
Angle of depression can be found using
any of the trigonometric functions.
ANGLE OF DEPRESSION

10. Example 1
Find the value of x.
Sin =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
ℎ𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒
sin 65° =
𝑥
200
𝑥 = (sin 65°) 200
𝑥 = 181.26 𝑚

11. Example 2
Solve the indicated measures.
tan =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 tan 42° =
2300
𝑦
tan 42° 𝑦 = 2300 𝑦 =
2300
tan 42°
𝑦 = 2554.41 𝑚

12. Example 2
Solve the indicated measures.
tan =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 tan 27° =
2300
𝑎
tan 27° 𝑎 = 2300 𝑎 =
2300
tan 27°
𝑦 = 2554.41 𝑚
𝑎 = 4514 𝑚
𝒂
𝑥 = 4514 − 2554.14
𝑎 = 𝑥 + 𝑦 4514 = 𝑥 + 2554.14
𝑥 = 1959.59

13. Example 3
From the top of a fire tower, a forest ranger sees his partner on the
ground at an angle of depression of 40°. If the tower is 45 feet in height
, how far is the partner from the base of the tower, to the nearest
hundredth of a foot?
tan =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 tan 40° =
45
𝑥
tan 40° 𝑥 = 45 𝑥 =
45
tan 40°
𝑥 = 53.63 𝑓𝑡

14. DO IT ON YOUR OWN
Jason is on the top of a 40- m cliff. He observes a boat is 80 m
away from the base of the cliff. Find the angle of depression of
the boat.
= 27°
𝑡𝑎𝑛 =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡

15. TEST YOURSELF
1. A 5- footer man standing 20 feet away from the tree, finds the angle of
elevation of the top of the tree to be 38 degree. How tall is the tree?
2. An airplane is flying at a height of 2 miles above the level ground. The angle of
depression of a tree from the plane is 15 degree. What is the distance the plane
must fly to be directly above the tree?
3. From the top of an 80- foot cliff, the angle of depression to a boat is 35 degree.
How far is the boat from the base of the cliff?