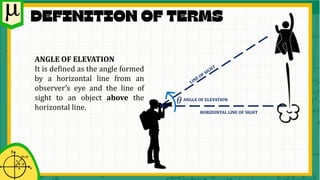
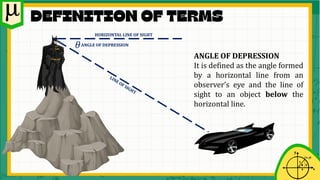
The document focuses on circular functions and their applications in trigonometry, particularly angles of elevation and depression. It includes definitions, properties of right triangles, and various example problems involving calculating heights and distances using trigonometric ratios. Students will learn to solve real-world problems related to angles and distances using these concepts.







![PRE-CALCULUS
1. A kite is flying with string inclined at 70 degrees to the horizon. What is
the height of the kite above the ground when the string is 86m long?
70°
86 𝑚eters
?
𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒
ℎ𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒
sin θ =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
ℎ𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒
sin 70° =
𝑦
86
[ ]
86 86
86 sin 70° = 𝑦
𝑦 = 𝟖𝟎. 𝟖𝟏 𝒎𝒆𝒕𝒆𝒓𝒔 𝒉𝒊𝒈𝒉](https://image.slidesharecdn.com/lesson2-250118142358-c6a9fbf3/85/Lesson-2-2-2-Angle-of-Elevation-and-Depression-pdf-10-320.jpg)
![PRE-CALCULUS
tan θ =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
tan 46° =
𝑦
23
[ ]
23 23
23 tan 46° = 𝑦
𝑦 = 𝟐𝟑. 𝟖𝟐 𝒎𝒆𝒕𝒆𝒓𝒔 𝒉𝒊𝒈𝒉
2. A tree casts a shadow 23 m long. The angle of elevation of a sun is 46
degrees. Find the height of the tree.
46°
23 𝑚eters
?
𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡](https://image.slidesharecdn.com/lesson2-250118142358-c6a9fbf3/85/Lesson-2-2-2-Angle-of-Elevation-and-Depression-pdf-11-320.jpg)
![PRE-CALCULUS
1. The angle of depression of a vehicle on the ground from the top of the tower
is 53 degrees. If the vehicle is at a distance of 120 meters away from the tower,
find the height of the tower.
53°
120 𝑚𝑒𝑡𝑒𝑟𝑠
?
tan θ =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
tan 53° =
𝑦
120
[ ]
120 120
120 tan 53° = 𝑦
𝑦 = 𝟏𝟓𝟗. 𝟐𝟒 𝒎𝒆𝒕𝒆𝒓𝒔 𝒉𝒊𝒈𝒉
𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡](https://image.slidesharecdn.com/lesson2-250118142358-c6a9fbf3/85/Lesson-2-2-2-Angle-of-Elevation-and-Depression-pdf-12-320.jpg)
![PRE-CALCULUS
2. From the top of a vertical cliff 40 m high, the angle of depression of an object
that is level with the base is 34 degrees. How far is the object from the base of
the cliff?
34°
40 𝑚
?
tan θ =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
tan 34° =
40
𝑥
[ ]
x x
x tan 34° = 40
𝑥 = 𝟓𝟗. 𝟑𝟎 𝒎𝒆𝒕𝒆𝒓𝒔
𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡
tan 34° tan 34°](https://image.slidesharecdn.com/lesson2-250118142358-c6a9fbf3/85/Lesson-2-2-2-Angle-of-Elevation-and-Depression-pdf-13-320.jpg)
![1. A man standing on a cliff sees two cars
approaching him on a road. The angles of
depression to the two cars from the man’s line of
sight are 25 and 40 respectively. If the height of
the cliff is 87 ft, find the distance between the two
cars.
25°
40°
87 𝑓𝑡
?
tan θ =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
tan 25° =
87
𝑥
[ ]
x x
x tan 25° = 87
𝑥1 = 186.57 𝒎𝒆𝒕𝒆𝒓𝒔
tan 25° tan 25°
tan θ =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
tan 40° =
87
𝑥
[ ]
x x
x tan 40° = 87
𝑥2 = 𝟏𝟎𝟑. 𝟔𝟖 𝒎𝒆𝒕𝒆𝒓𝒔
tan 40° tan 40°
186.57 m −𝟏𝟎𝟑. 𝟔𝟖 𝒎 = 𝟖𝟐. 𝟖𝟗 𝒎](https://image.slidesharecdn.com/lesson2-250118142358-c6a9fbf3/85/Lesson-2-2-2-Angle-of-Elevation-and-Depression-pdf-14-320.jpg)
![2. A photographer who is 6 foot tall is standing
away from the base of a 60-foot tall building. The
photographer looks up to the top of the building
and measures the angle of elevation to be 53.47
degrees. How far is the photographer from the
building?
53.47°
60 𝑓𝑡
tan θ =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
tan 53.47° =
54
𝑥
[ ]
x x
x tan 53.47° = 54
𝑥 = 40 𝒎𝒆𝒕𝒆𝒓𝒔
tan 53.47° tan 53.47°
?
60 − 6 = 54 ft](https://image.slidesharecdn.com/lesson2-250118142358-c6a9fbf3/85/Lesson-2-2-2-Angle-of-Elevation-and-Depression-pdf-15-320.jpg)
![3. A hospital has a wheelchair ramp leading up to
its entrance. The entrance is 5 feet above ground
level, and the ramp is designed to make an angle
of elevation of 15 degrees with the ground. How
long is the ramp?
sin θ =
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
ℎ𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒
sin 15° =
5
𝑟
[ ]
r r
r sin 15° = 5
𝑟 = 19.32 𝒇𝒕
sin 15° sin 15°
𝟏𝟓° ]5 ft
Idea:
?](https://image.slidesharecdn.com/lesson2-250118142358-c6a9fbf3/85/Lesson-2-2-2-Angle-of-Elevation-and-Depression-pdf-16-320.jpg)