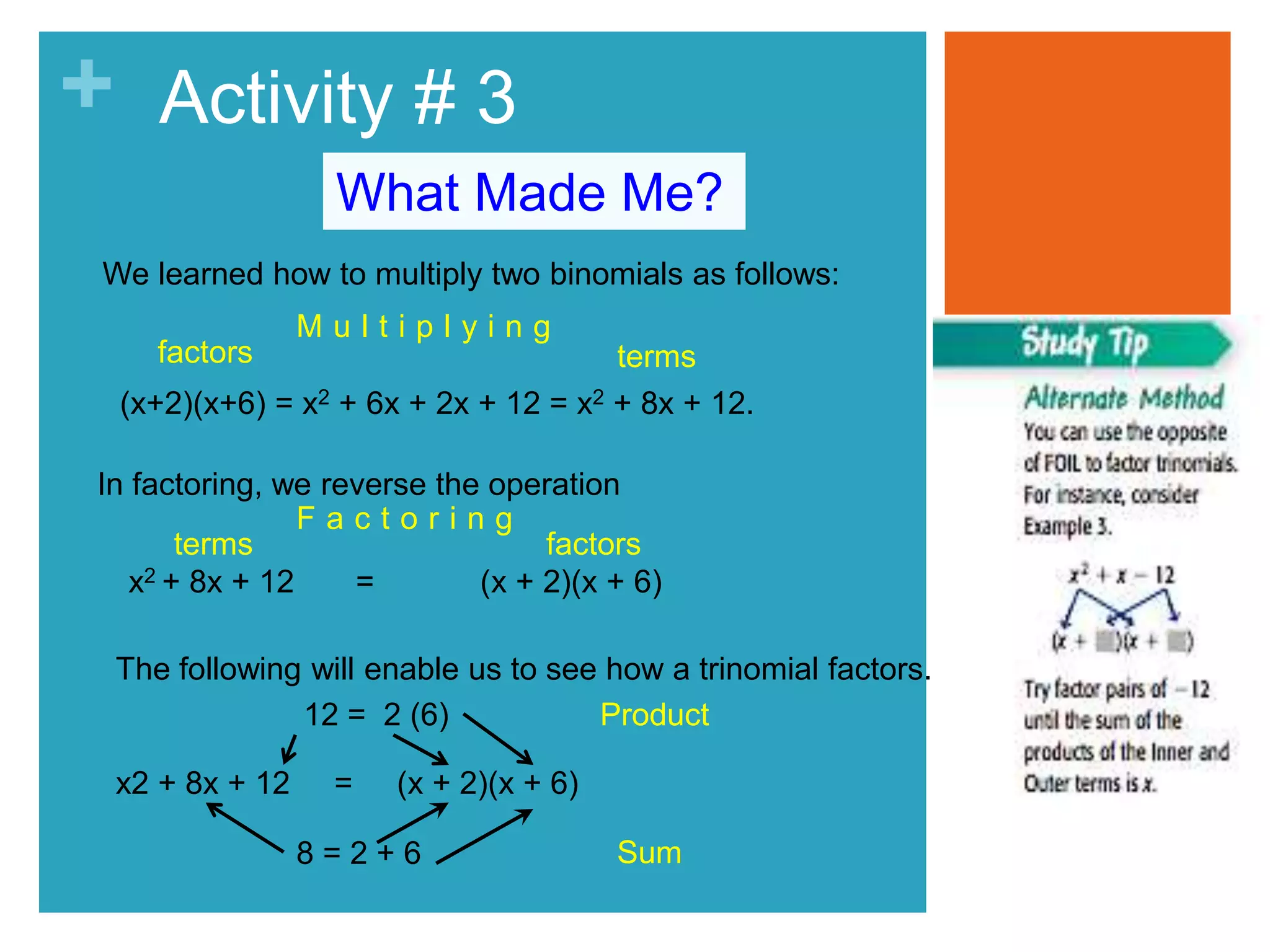
This document provides an overview and activities on solving quadratic equations by factoring. It begins by defining quadratic equations and their standard form. Several activities are presented to practice identifying quadratic equations, rewriting them in standard form, and factoring trinomials of the form x^2 + bx + c. The final activity involves factoring quadratic equations to determine their roots. The document aims to build mastery of skills needed to solve quadratic equations using factoring techniques.

1. +
Strategic
Intervention
Material
Mathematics IX
Solving Quadratic Equation by Factoring
Prepared by: Brian M. Mary T-I

2. LEAST MASTERED SKILLS
Solving Quadratic Equation by Factoring
Sub Tasks
+
 Identifying quadratic equations
 Rewriting quadratic equations to its standard form
 Factor trinomials in the form x2 + bx + c
 Determine roots of quadratic equation
ax2 + bx + c = 0, by factoring

3. +
Overview
A quadratic equation in one variable is a
mathematical sentence of degree 2 that
can be written in the following form
ax2 + bx + c = 0,
where a, b, and c are real numbers and
a ≠ 0.
How are quadratic equations used in
solving real – life problems and in
making decisions?
Many formulas used in the
physical world are quadratic in
nature since they become
second-degree equations when
solving for one of the variables.
Likewise, many word problems
require the use of the quadratic
equation.
At the enrichment card, we
will consider some of the
common uses of the quadratic
equations.

4. + Activity # 1
Quadratic or Not Quadratic?
Direction. Identify which of the following equations are
quadratic and which are not. Write QE if the equations
are quadratic and NQE if not quadratic equation.
__________ 1. 3m + 8 = 15
__________ 2. x2 – 5x – 10 = 0
__________ 3. 2t2 – 7t = 12
__________ 4. 12 – 4x = 0
__________ 5. 25 – r2 = 4r

5. Activity # 2
+
Set Me to Your Standard!
Direction. Write each quadratic equation in standard
form, ax2 + bx + c = 0.
 1. 3x – 2x2 = 7
____________________
 2. 5 – 2r2 = 6r
____________________
 3. 2x(x – 3) = 15
____________________
 4. (x + 3)(x + 4)= 0
____________________
 5. (x + 4)2 + 8 = 0

6. + Activity # 3
What Made Me?
We learned how to multiply two binomials as follows:
factors
terms
M u l t i p l y i n g
(x+2)(x+6) = x2 + 6x + 2x + 12 = x2 + 8x + 12.
In factoring, we reverse the operation
F a c t o r i n g
terms factors
x2 + 8x + 12 = (x + 2)(x + 6)
The following will enable us to see how a trinomial factors.
12 = 2 (6)
x2 + 8x + 12 = (x + 2)(x + 6)
8 = 2 + 6
Product
Sum

7. In general, the trinomial x2 + bx + c will factor only if there are two
integers, which will we call m and n, such that m + n = b and
m(n) = c.
+
Sum Product
m + n m(n)
x2 + bx + c = (x + m)(x + n)
1. a2 + 11a + 18 m + n = 11 m(n) = 18
2 + 9 = 11 2(9) = 18
The m and n values are 2 and 9. the factorization is,
a2 + 11a + 18 = (x + 2) (x + 9)
2. b2 – 2b – 15 m + n = - 2 m(n) = - 15
3 + (-5) = - 2 3(-5) = - 15
The m and n values are 3 and - 5. the factorization is,
b2 – 2b – 15 = (x + 3) (x – 5)

8. Factor the following trinomial in the form x2 + bx + c.
x2 + bx + c m + n m(n) (x + m)(x + n)
x2 + 4x – 12 6 + (-2) 6(-2) (x + 6)(x – 2)
w2 – 8w + 12
x2 + 5x - 24
c2 + 6c + 5
+
r2 + 5r – 14
x2 + 5x + 7
After learning how to factor trinomial in the form x2 + bx + c,
we will now determine roots of a quadratic equation using factoring.

9. Activity # 4
+
Factor then Solve!
Some quadratic equations can be solved easily by factoring. To solve each equations, the
following procedures can be followed.
1. Transform the quadratic equation into standard form if necessary.
2. Factor the quadratic expression.
3. Set each factor of the quadratic expression equal to 0.
4. Solve each resulting equation.
Example. Find the solution of x2 + 9x = -8 by factoring.
a. Transform the equation into standard form
x2 + 9x = -8  x2 + 9x + 8 = 0
b. Factor the quadratic expression
x2 + 9x + 8 = 0  (x + 1)(x +8) = 0
c. Set each factor equal to 0.
(x + 1)(x + 8) = 0  x + 1 = 0; x + 8 = 0
d. Solve each resulting equation.
x + 1 = 0  x + 1 – 1 = 0 -
1
x = - 1
x + 8 = 0  x + 8 – 8 = 0 - 8
x = - 8

10. Direction. Determine the roots of the following quadratic equations using factoring.
1. x2 + 8x + 16 = 0 _____________________________________
+
_____________________________________
_____________________________________
2. x2 – 9x – 14 = 0 _____________________________________
_____________________________________
_____________________________________
3. y2 + 9y + 20 = 0 _____________________________________
_____________________________________
_____________________________________
4. b2 – 10b + 21 = 0 _____________________________________
_____________________________________
_____________________________________

11. Number Theory
* The product of two consecutive even numbers is 168. What are the integers?
Solution: Let x = the lesser even integer. Then, x + 2 = the next consecutive even integer.
Note: Consecutive even or odd integers are given by x, x+ 2, x + 4, …
product of two consecutive even integers is 168
x2 + 2x = 168 original equation
x2 + 2x – 168 = 0 write in standard form
+
x ( x + 2 ) = 168
( x + 14 ) ( x – 12 ) = 0 factor the left member
x + 14 = 0 or x – 12 = 0 set each factor equal to zero
x = - 14 x = 12 solve each equation
when x = - 14, then x + 2 = - 14 + 2 = - 12 and when x = 12, then x + 2 = 12 + 2 = 14
since (-14)(-12) = 168 and (12)(14) = 168, and both solutions are consecutive even integers, the
conditions of the problem are met.
Therefore, the two integers are – 14 and – 12 or 12 and 14.
Mastery Points!
Can you
 Determine two integers whose product is one number and whose sum is another number?
Recognize when the trinomial x2 + bx + c will factor and when it will not?
Factor trinomial of the form x2 + bx +c ?
Determine roots of a quadratic function in the form ax2 + bx + c?

12. Learner’s Material – Mathematics IX, First Edition pp. 27 - 34
Holiday, Berchie. et. al. ALGEBRA 2. USA. The McGraw – Hill
Companies, C2008. pp. 253 – 256
Wesner, et. al. ELEMENTARY ALGEBRA with APPLICATIONS.
Bernard +
J. Klein Publishing, 2006
pp. 152 – 156

13. Activity # 1 Quadratic or Not Quadratic?
+
1. NQE
2. QE
3. QE
4. NQE
5. QE
Activity # 2 Set Me to Your Standard
1. - 2x2 + 3x – 7 = 0/2x2 – 3x + 7 = 0
2. - 2r2 – 6r + 5 = 0/2r2 + 6r – 5 = 0
3. 2x2 – 6x – 15 = 0
4. x2 + 7x + 12 = 0
5. x2 + 8x + 24 = 0
Activity # 3 What Made Me?
x2 + bx + c m + n m(n) (x + m) (x + n)
w2 – 8w + 12 - 6 + 2 -6(2) (w – 6)(w + 2)
x2 + 5x – 24 8 + (-3) 8(-3) (x + 8)(x – 3)
c2 + 6c + 5 5 + 1 5(1) (c + 5)(c + 1)
r2 + 5r – 14 7 + (-2) 7(-2) (r + 7)(r – 2)
x2 + 9x + 20 5 + 4 5(4) (x + 5)(x + 4)
Assessment
1. x2 + 8x + 16 = 0 (x + 4)(x + 4) = 0
x + 4 = 0
x + 4 – 4 = 0 – 4
x = - 4
2. x2 – 5x – 14 = 0 (x – 7)(x – 2) = 0
x – 7 = 0 x – 2 = 0
x – 7 + 7 = 0 + 7 x – 2 + 2 = 0 + 2
x = 7 x = 2
3. y2 + 9y + 20 = 0 (y + 5)(y + 4) = 0
y + 5 = 0 y + 4 = 0
y + 5 – 5 = 0 – 5 y + 4 – 4 = 0 – 4
y = - 5 y = - 4
4. b2 – 10b + 21 = 0 (b – 7)(b – 3) = 0
b – 7 = 0 b – 3 = 0
b – 7 + 7 = 0 + 7 b – 3 + 3 = 0 + 3
b = 7 b = 3

14. +