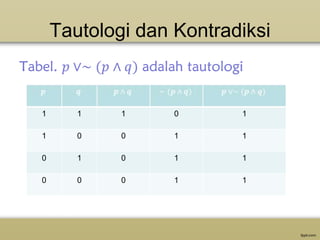
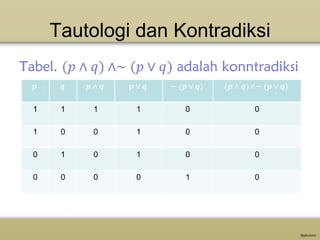
Dokumen ini menjelaskan tentang logika, termasuk definisi dan pentingnya, serta berbagai jenis penalaran seperti logika simbolik, proposisi, dan perangkai dasar. Terdapat penjabaran tentang simbol-simbol yang digunakan dalam logika dan juga contoh-contoh pernyataan yang berkaitan dengan implikasi, tautologi, dan kontradiksi. Selain itu, dokumen ini memberikan latihan dan tugas untuk menerapkan konsep logika dalam kalimat-kalimat tertentu.