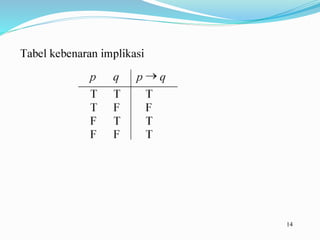
Pertemuan membahas operasi logika proposisi seperti konjungsi, disjungsi, negasi, implikasi, dan biimplikasi. Terdapat latihan membuat tabel kebenaran dan mengevaluasi proposisi majemuk seperti tautologi dan kontradiksi. Dibahas pula proposisi bersyarat, varian implikasi, dan biimplikasi beserta contoh-contohnya. Terdapat pula penjelasan mengenai argumen-argumen yang sudah terbukti sahih secar