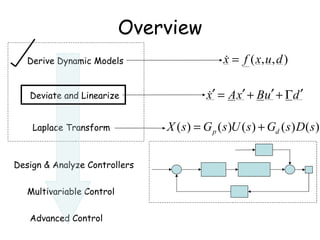
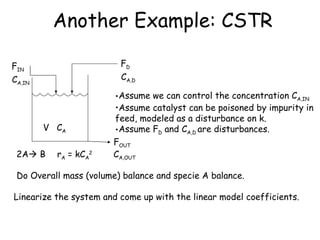
Linearization involves developing a linear approximation of a nonlinear system around an operating point. This allows tools from linear systems theory to be applied to analyze and design controllers for nonlinear systems. Specifically, Taylor's theorem is used to expand the nonlinear functions as a linear combination of deviations from the operating point. The resulting linearized model is only valid locally but provides an approximate way to analyze system behavior if well-controlled near the operating point. Examples show how to derive linearized models for common nonlinear systems like tanks and chemical reactors.

1. Linearization Why linearization? What is linearization? Doing Linearization

2. Overview Derive Dynamic Models Deviate and Linearize Laplace Transform Design & Analyze Controllers Multivariable Control Advanced Control

3. Why Linearize? Classical linear systems theory applies only to linear systems. Therefore we linearize to enable approximate analysis of system behavior. Do we solve the exact problem approximately or an approximate problem exactly? Philosophically: Practically: If we are doing a good job of controlling the system around a steady state, then our linearization around that steady state will be a good approximation. There are no real alternatives, non-linear systems theory does not go very far.

4. What is Linearization? Development of a linear approximation to an ODE system. What is linear? When a variable appears multiplied ONLY by a constant. 5x is linear 5xy is non linear 5x 1/2 is non linear Consider a simple case of an ODE (one state variable x) and a single input variable u. x ss Linearization

5. Linearization Use Taylor’s Theorem to expand the function around the steady state point Partial Derivatives EVALUATED at steady state, just numbers Now it is convenient to use deviation from steady state as our description Let Subtract from above linearized equation

6. Example F IN h F OUT Gravity Draining Tank open to atmosphere Constant Density Substitute expression Linearize:

7. Extensions Linearization of derivative terms Still not linear because it is the multiplication of two variables. 0 Note in general that we will substitute for one of the derivative terms BEFORE we linearize, but we will still need the expression for the remaining derivative.

8. Another Example: CSTR V F OUT F IN C A,IN C A,OUT C A F D C A,D 2A  B r A = kC A 2 Assume we can control the concentration C A,IN Assume catalyst can be poisoned by impurity in feed, modeled as a disturbance on k. Assume F D and C A,D are disturbances. Do Overall mass (volume) balance and specie A balance. Linearize the system and come up with the linear model coefficients.