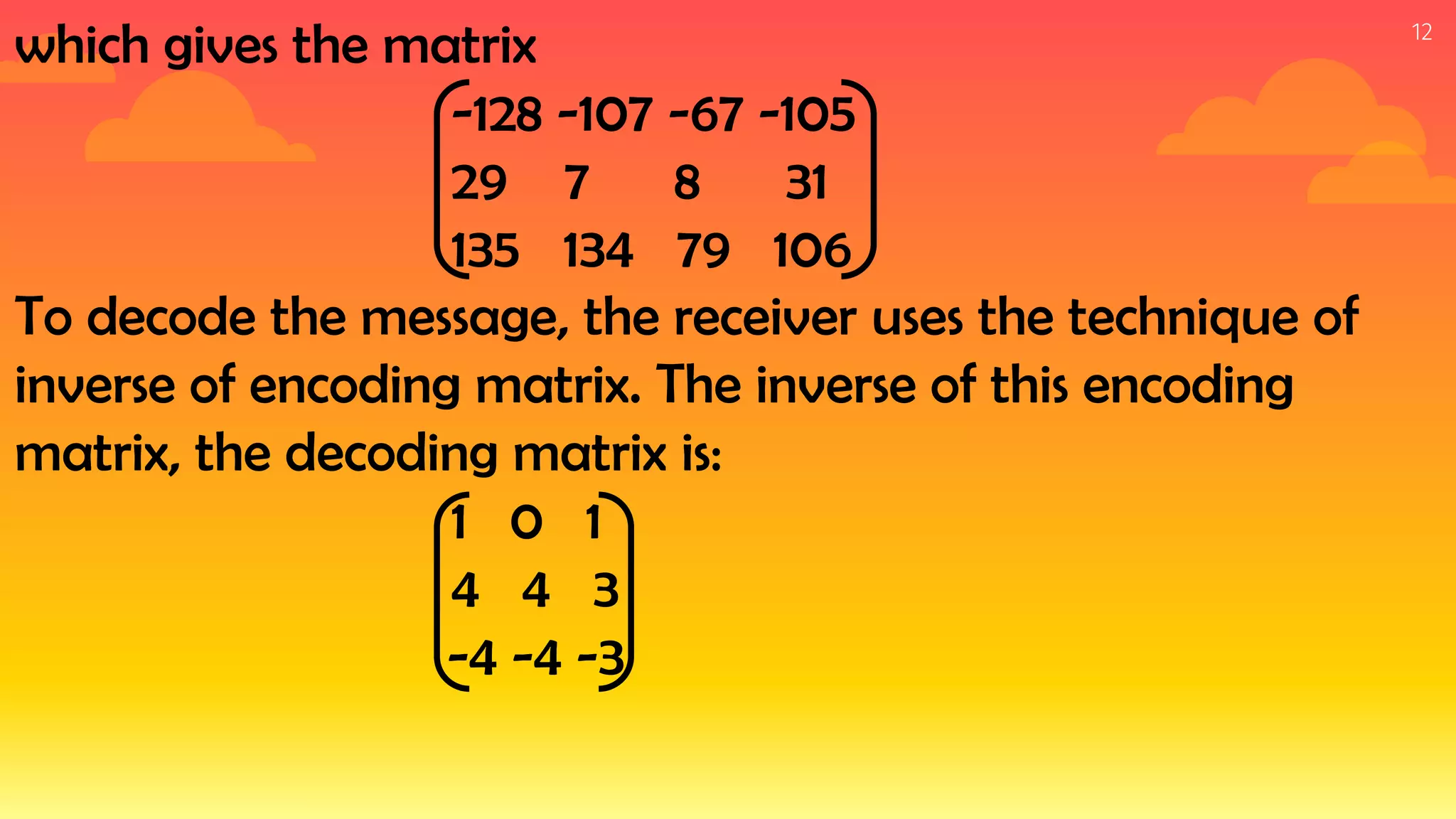
Linear algebra has applications in balancing chemical equations, cryptography, and geometry. Balancing chemical equations involves setting up a linear system to satisfy the law of conservation of mass such that the number of atoms is equal on both sides of the equation. Cryptography uses linear algebra operations like matrix multiplication for encryption and decryption of messages. In geometry, finding the equation of a circle through three points involves setting up a homogeneous linear system and calculating the determinant to obtain the equation of the circle.