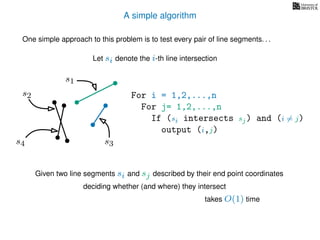
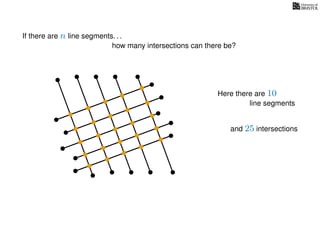
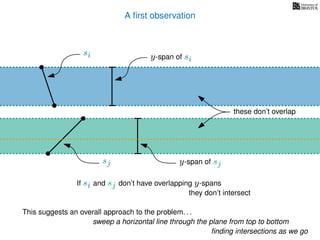
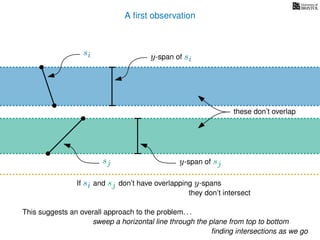
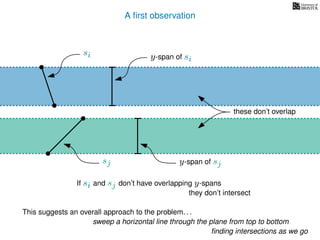
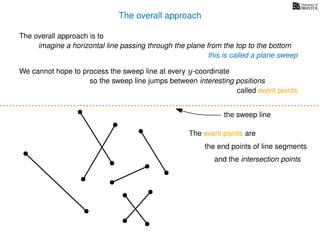
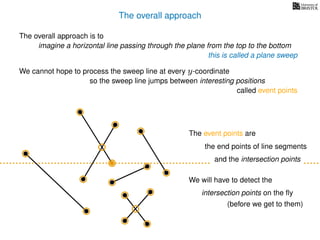
The document discusses the problem of finding all intersections between n line segments in a plane. It presents a basic algorithm that checks each pair of line segments for intersections, running in O(n^2) time, as well as a more efficient 'sweep line' approach that operates in O(n log n + k log n) time, considering the number of intersections k. Additionally, it emphasizes distinguishing segments based on their y-spans to determine potential intersections.

1. Data Structures and Algorithms – COMS21103
Line Segment Intersections
Benjamin Sach
slides inspired by Marc van Kreveld

2. Introduction
Problem Given n line segments, find all the intersections. . .

3. Introduction
Problem Given n line segments, find all the intersections. . .
intersection

4. Introduction
Problem Given n line segments, find all the intersections. . .
In the input, each line segment is given by
the coordinates of its end points
intersection

5. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3

6. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3

7. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3

8. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3

9. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3

10. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3

11. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3

12. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3

13. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3

14. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3

15. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3
intersection found

16. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3

17. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3

18. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3

19. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3
Given two line segments si and sj described by their end point coordinates
deciding whether (and where) they intersect
takes O(1) time

20. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3
Given two line segments si and sj described by their end point coordinates
deciding whether (and where) they intersect
takes O(1) time
Why?

21. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3
Given two line segments si and sj described by their end point coordinates
deciding whether (and where) they intersect
takes O(1) time
Why?
Any computation on two objects with O(1) space descriptions takes O(1) time

22. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3

23. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3
This algorithm runs in O(n2) time
(because checking pair of lines takes O(1) time)

24. A simple algorithm
One simple approach to this problem is to test every pair of line segments. . .
For i = 1,2,...,n
For j= 1,2,...,n
If (si intersects sj) and (i = j)
output (i,j)
Let si denote the i-th line intersection
s2
s4
s1
s3
This algorithm runs in O(n2) time
(because checking pair of lines takes O(1) time)
. . . can we do better?

26. If there are n line segments. . .
how many intersections can there be?

27. If there are n line segments. . .
how many intersections can there be?
Here there are 10
line segments
and 25 intersections

28. If there are n line segments. . .
how many intersections can there be?
Here there are 50
line segments
and 625 intersections

29. If there are n line segments. . .
how many intersections can there be?
Here there are 50
line segments
and 625 intersections
In general, there could be
( n
2 )2 intersections
more than

30. If there are n line segments. . .
how many intersections can there be?
Here there are 50
line segments
and 625 intersections
In general, there could be
( n
2 )2 intersections
If we want to output all the intersections,
we can’t possibly expect to do better than O(n2) time in the worst-case
more than

31. Output sensitive algorithms
The time complexities of the algorithms we have seen so far (in this course)
have only depended on the size on the input

32. Output sensitive algorithms
The time complexities of the algorithms we have seen so far (in this course)
have only depended on the size on the input
The time complexity of the algorithm we will see in this lecture
also depends on the size of the output

33. Output sensitive algorithms
The time complexities of the algorithms we have seen so far (in this course)
have only depended on the size on the input
The time complexity of the algorithm we will see in this lecture
also depends on the size of the output
Let k denote the number of line segment intersections
(k is not provided in the input)

34. Output sensitive algorithms
The time complexities of the algorithms we have seen so far (in this course)
have only depended on the size on the input
The time complexity of the algorithm we will see in this lecture
also depends on the size of the output
Let k denote the number of line segment intersections
(k is not provided in the input)
Here n = 17
and k = 3

35. Output sensitive algorithms
The time complexities of the algorithms we have seen so far (in this course)
have only depended on the size on the input
The time complexity of the algorithm we will see in this lecture
also depends on the size of the output
Let k denote the number of line segment intersections
(k is not provided in the input)
We will see an algorithm for line segment intersection which takes
O(n log n + k log n) time in the worst-case
Here n = 17
and k = 3

36. Output sensitive algorithms
We will see an algorithm for line segment intersection which takes
If k is small. . .
For example if k 2n we get an
If k is big. . .
O(n log n) worst-case time
For example if k ( n
2 )2 we get an
O(n2 log n) worst-case time
(which is worse than the simple algorithm)
O(n log n + k log n) time in the worst-case

37. Some simplifying restrictions
All of these restrictions can be removed making the algorithm slightly more involved
(without changing the time complexity)
In the interest of simplicity, we don’t allow the input to contain any of the following:
three (or more)
which intersect at
the same point
horizontal line segments
two end points
with the same y-coordinate
lines segments
overlapping
line segments

38. A first observation

39. A first observation
si

40. A first observation
si y-span of si

41. A first observation
si y-span of si
sj

42. A first observation
si y-span of si
sj y-span of sj

43. A first observation
si y-span of si
sj y-span of sj
If si and sj don’t have overlapping y-spans
they don’t intersect

44. A first observation
si y-span of si
sj y-span of sj
If si and sj don’t have overlapping y-spans
they don’t intersect
these don’t overlap

45. A first observation
si y-span of si
sj y-span of sj
If si and sj don’t have overlapping y-spans
they don’t intersect
these don’t overlap
This suggests an overall approach to the problem. . .

46. A first observation
si y-span of si
sj y-span of sj
If si and sj don’t have overlapping y-spans
they don’t intersect
these don’t overlap
This suggests an overall approach to the problem. . .
sweep a horizontal line through the plane from top to bottom
finding intersections as we go

47. A first observation
si y-span of si
sj y-span of sj
If si and sj don’t have overlapping y-spans
they don’t intersect
these don’t overlap
This suggests an overall approach to the problem. . .
sweep a horizontal line through the plane from top to bottom
finding intersections as we go

48. A first observation
si y-span of si
sj y-span of sj
If si and sj don’t have overlapping y-spans
they don’t intersect
these don’t overlap
This suggests an overall approach to the problem. . .
sweep a horizontal line through the plane from top to bottom
finding intersections as we go

49. A first observation
si y-span of si
sj y-span of sj
If si and sj don’t have overlapping y-spans
they don’t intersect
these don’t overlap
This suggests an overall approach to the problem. . .
sweep a horizontal line through the plane from top to bottom
finding intersections as we go

50. A first observation
si y-span of si
sj y-span of sj
If si and sj don’t have overlapping y-spans
they don’t intersect
these don’t overlap
This suggests an overall approach to the problem. . .
sweep a horizontal line through the plane from top to bottom
finding intersections as we go

51. A first observation
si y-span of si
sj y-span of sj
If si and sj don’t have overlapping y-spans
they don’t intersect
these don’t overlap
This suggests an overall approach to the problem. . .
sweep a horizontal line through the plane from top to bottom
finding intersections as we go

52. A first observation
si y-span of si
sj y-span of sj
If si and sj don’t have overlapping y-spans
they don’t intersect
these don’t overlap
This suggests an overall approach to the problem. . .
sweep a horizontal line through the plane from top to bottom
finding intersections as we go

53. A first observation
si y-span of si
sj y-span of sj
If si and sj don’t have overlapping y-spans
they don’t intersect
these don’t overlap
This suggests an overall approach to the problem. . .
sweep a horizontal line through the plane from top to bottom
finding intersections as we go

54. A first observation
si y-span of si
sj y-span of sj
If si and sj don’t have overlapping y-spans
they don’t intersect
these don’t overlap
This suggests an overall approach to the problem. . .
sweep a horizontal line through the plane from top to bottom
finding intersections as we go

55. A first observation
si y-span of si
sj y-span of sj
If si and sj don’t have overlapping y-spans
they don’t intersect
these don’t overlap
This suggests an overall approach to the problem. . .
sweep a horizontal line through the plane from top to bottom
finding intersections as we go

56. A first observation
si y-span of si
sj y-span of sj
If si and sj don’t have overlapping y-spans
they don’t intersect
these don’t overlap
This suggests an overall approach to the problem. . .
sweep a horizontal line through the plane from top to bottom
finding intersections as we go

57. Adjacent line segments and a second observation
These two line segments
are adjacent at this y-coordinate

58. Adjacent line segments and a second observation
These two line segments
are adjacent at this y-coordinate
(there is no line segment between them)

59. Adjacent line segments and a second observation

60. Adjacent line segments and a second observation
These two line segments

61. Adjacent line segments and a second observation
These two line segments
are adjacent at this y-coordinate

62. Adjacent line segments and a second observation
These two line segments
are adjacent at this y-coordinate
but they aren’t adjacent at this y-coordinate

63. Adjacent line segments and a second observation

64. Adjacent line segments and a second observation
These two line segments

65. Adjacent line segments and a second observation
These two line segments
never become adjacent

66. Adjacent line segments and a second observation
These two line segments
never become adjacent
so they can’t intersect

67. Adjacent line segments and a second observation
These two line segments
never become adjacent
so they can’t intersect
Two line segments si and sj which are never adjacent don’t intersect

68. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep

69. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
the sweep line

70. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
the sweep line

71. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
the sweep line
The event points are
the end points of line segments
and the intersection points

72. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points

73. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points

74. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points

75. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points

76. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points

77. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)

78. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)

79. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)

80. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)

81. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)

82. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)

83. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)

84. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)

85. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)

86. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)

87. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)

88. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)

89. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)

90. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)

91. The overall approach
The overall approach is to
imagine a horizontal line passing through the plane from the top to the bottom
this is called a plane sweep
We cannot hope to process the sweep line at every y-coordinate
so the sweep line jumps between interesting positions
called event points
The event points are
the end points of line segments
and the intersection points
We will have to detect the
intersection points on the fly
(before we get to them)
The number of event points is O(n + k)

92. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )

93. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
this is first this is last
(i.e. in the order given by the )

94. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )

95. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
Fact the status of the sweep line can only change at event points
(i.e. at an end point or an intersection)

96. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
Fact the status of the sweep line can only change at event points
(i.e. at an end point or an intersection)

97. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
Fact the status of the sweep line can only change at event points
(i.e. at an end point or an intersection)
the move but the order stays the same

98. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
Fact the status of the sweep line can only change at event points
(i.e. at an end point or an intersection)
the move but the order stays the same

99. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
Fact the status of the sweep line can only change at event points
(i.e. at an end point or an intersection)
the move but the order stays the same
We will store the status of the sweep line in a data structure
which allows efficient updates (more details later)

100. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )

101. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
The status of the sweep line tells us which line segments are currently adjacent

102. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
Why is this useful?
The status of the sweep line tells us which line segments are currently adjacent

103. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
Why is this useful?
The status of the sweep line tells us which line segments are currently adjacent
two line segments which never become adjacent cannot intersect

104. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
Why is this useful?
The status of the sweep line tells us which line segments are currently adjacent
two line segments which never become adjacent cannot intersect
We will detect each upcoming intersection when
the corresponding line segments first become adjacent

105. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
Why is this useful?
The status of the sweep line tells us which line segments are currently adjacent
two line segments which never become adjacent cannot intersect
We will detect each upcoming intersection when
the corresponding line segments first become adjacent
we will detect this

106. The status of the sweep line
The status of the sweep line
is the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
Why is this useful?
The status of the sweep line tells us which line segments are currently adjacent
two line segments which never become adjacent cannot intersect
We will detect each upcoming intersection when
the corresponding line segments first become adjacent
we will detect this
when the sweep line stops here

107. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure

108. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure

109. Updating the sweep line
Every time the sweep line moves to the next event point, we update
If the event point is
the top of a line segment, we insert it into the status data structure
(at the appropriate place)
the status data structure

110. Updating the sweep line
Every time the sweep line moves to the next event point, we update
If the event point is
the top of a line segment, we insert it into the status data structure
(at the appropriate place)
insert this
the status data structure

111. Updating the sweep line
Every time the sweep line moves to the next event point, we update
If the event point is
the top of a line segment, we insert it into the status data structure
(at the appropriate place)
We then check whether this segment will intersect either of the adjacent segments
insert this
the status data structure

112. Updating the sweep line
Every time the sweep line moves to the next event point, we update
If the event point is
the top of a line segment, we insert it into the status data structure
(at the appropriate place)
We then check whether this segment will intersect either of the adjacent segments
the status data structure

113. Updating the sweep line
Every time the sweep line moves to the next event point, we update
If the event point is
the top of a line segment, we insert it into the status data structure
(at the appropriate place)
We then check whether this segment will intersect either of the adjacent segments
will these intersect?
the status data structure

114. Updating the sweep line
Every time the sweep line moves to the next event point, we update
If the event point is
the top of a line segment, we insert it into the status data structure
(at the appropriate place)
We then check whether this segment will intersect either of the adjacent segments
will these intersect?
the status data structure

115. Updating the sweep line
Every time the sweep line moves to the next event point, we update
If the event point is
the top of a line segment, we insert it into the status data structure
(at the appropriate place)
We then check whether this segment will intersect either of the adjacent segments
If either pair will intersect, we’ve found a new event point
will these intersect?
the status data structure

116. Updating the sweep line
Every time the sweep line moves to the next event point, we update
If the event point is
the top of a line segment, we insert it into the status data structure
(at the appropriate place)
We then check whether this segment will intersect either of the adjacent segments
If either pair will intersect, we’ve found a new event point
the status data structure

117. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure

118. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure

119. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is
the bottom of a line segment, we delete it from the status data structure

120. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is
the bottom of a line segment, we delete it from the status data structure
delete this

121. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is
the bottom of a line segment, we delete it from the status data structure

122. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is
the bottom of a line segment, we delete it from the status data structure
This makes a pair of segments adjacent, so we check whether they will intersect

123. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is
the bottom of a line segment, we delete it from the status data structure
This makes a pair of segments adjacent, so we check whether they will intersect

124. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is
the bottom of a line segment, we delete it from the status data structure
This makes a pair of segments adjacent, so we check whether they will intersect
will these intersect?

125. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is
the bottom of a line segment, we delete it from the status data structure
This makes a pair of segments adjacent, so we check whether they will intersect
a new event
point
will these intersect?

126. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is
the bottom of a line segment, we delete it from the status data structure
This makes a pair of segments adjacent, so we check whether they will intersect
If they will intersect, we’ve found a new event point
a new event
point
will these intersect?

127. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure

128. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure

129. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is
an intersection point, we swap the two line segments in the status data structure

130. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is
an intersection point, we swap the two line segments in the status data structure
BEFORE
AFTER

131. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is
an intersection point, we swap the two line segments in the status data structure
BEFORE
AFTER
This gives two new pairs of adjacent segments to check

132. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is
an intersection point, we swap the two line segments in the status data structure
BEFORE
AFTER
This gives two new pairs of adjacent segments to check

133. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is
an intersection point, we swap the two line segments in the status data structure
BEFORE
AFTER
This gives two new pairs of adjacent segments to check

134. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is
an intersection point, we swap the two line segments in the status data structure
BEFORE
AFTER
This gives two new pairs of adjacent segments to check
If either pair will intersect, we’ve found a new event point

135. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure

136. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is:
the top of a line segment, we insert it into the status data structure

137. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
If the event point is:
the bottom of a line segment, we delete it from the status data structure
the top of a line segment, we insert it into the status data structure

138. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
an intersection point, we swap the two line segments in the status data structure
If the event point is:
the bottom of a line segment, we delete it from the status data structure
the top of a line segment, we insert it into the status data structure

139. Updating the sweep line
Every time the sweep line moves to the next event point, we update
the status data structure
an intersection point, we swap the two line segments in the status data structure
If the event point is:
the bottom of a line segment, we delete it from the status data structure
the top of a line segment, we insert it into the status data structure
and we always check whether we have discovered any new event points
(specifically intersections)

140. How do we keep track of the event points?
At the start of the algorithm,
we are aware of 2n event points,
one for each end of each line segment

141. How do we keep track of the event points?
At the start of the algorithm,
we are aware of 2n event points,
one for each end of each line segment
The sweep line starts at the top event point
(the one with the highest y value)

142. How do we keep track of the event points?
At the start of the algorithm,
we are aware of 2n event points,
one for each end of each line segment
The sweep line starts at the top event point
After processing an event point,
(the one with the highest y value)
the sweep line moves down
to the next event point

143. How do we keep track of the event points?
At the start of the algorithm,
we are aware of 2n event points,
one for each end of each line segment
The sweep line starts at the top event point
After processing an event point,
(the one with the highest y value)
the sweep line moves down
to the next event point
However, in processing an event point,
the algorithm may discover new event points
(specifically intersections)

144. How do we keep track of the event points?
At the start of the algorithm,
we are aware of 2n event points,
one for each end of each line segment
The sweep line starts at the top event point
After processing an event point,
(the one with the highest y value)
the sweep line moves down
to the next event point
However, in processing an event point,
the algorithm may discover new event points
(specifically intersections)
We keep track of the event points using a Priority Queue

145. How do we keep track of the event points?
At the start of the algorithm,
we are aware of 2n event points,
one for each end of each line segment
The sweep line starts at the top event point
After processing an event point,
(the one with the highest y value)
the sweep line moves down
to the next event point
However, in processing an event point,
the algorithm may discover new event points
(specifically intersections)
We keep track of the event points using a Priority Queue
Every event point is INSERTED as it is discovered (with its y value as the key)

146. How do we keep track of the event points?
At the start of the algorithm,
we are aware of 2n event points,
one for each end of each line segment
The sweep line starts at the top event point
After processing an event point,
(the one with the highest y value)
the sweep line moves down
to the next event point
However, in processing an event point,
the algorithm may discover new event points
(specifically intersections)
We keep track of the event points using a Priority Queue
Every event point is INSERTED as it is discovered (with its y value as the key)
We can then use DELETEMIN to recover the next event point

147. Can we miss out on an intersection?
si
sj
If si and sj intersect
they must become adjacent at some y-coordinate
(before they intersect)

148. Can we miss out on an intersection?
si
sj
If si and sj intersect
they must become adjacent at some y-coordinate
(before they intersect)
In particular, they must become adjacent at some event point
with a higher y-coordinate

149. Can we miss out on an intersection?
si
sj
If si and sj intersect
they must become adjacent at some y-coordinate
(before they intersect)
In particular, they must become adjacent at some event point
with a higher y-coordinate

150. Can we miss out on an intersection?
si
sj
If si and sj intersect
they must become adjacent at some y-coordinate
(before they intersect)
This is because the status of the sweep line doesn’t change between event points
In particular, they must become adjacent at some event point
with a higher y-coordinate

151. Can we miss out on an intersection?
si
sj
If si and sj intersect
they must become adjacent at some y-coordinate
(before they intersect)
This is because the status of the sweep line doesn’t change between event points
In particular, they must become adjacent at some event point
with a higher y-coordinate
The formal proof then follows by induction

152. Can we find the same event point twice?
Consider the line segments shown. . .

153. Can we find the same event point twice?
Consider the line segments shown. . .

154. Can we find the same event point twice?
Consider the line segments shown. . .
when we process this event point,

155. Can we find the same event point twice?
Consider the line segments shown. . .
we discover this event point
when we process this event point,

156. Can we find the same event point twice?
Consider the line segments shown. . .
we rediscover this event point
when we process this event point,

157. Can we find the same event point twice?
Consider the line segments shown. . .
we rediscover this event point
again
when we process this event point,

158. Can we find the same event point twice?
Consider the line segments shown. . .
we rediscover this event point
again
and again

159. Can we find the same event point twice?

160. Can we find the same event point twice?
That is, we can discover
the same event point more than once

161. Can we find the same event point twice?
That is, we can discover
the same event point more than once
There are (at least) two ways to deal with this:

162. Can we find the same event point twice?
That is, we can discover
the same event point more than once
There are (at least) two ways to deal with this:
1. Check whether we already found the new point
- by looking it up in the priority queue

163. Can we find the same event point twice?
That is, we can discover
the same event point more than once
There are (at least) two ways to deal with this:
1. Check whether we already found the new point
- by looking it up in the priority queue
2. Don’t worry about it (INSERT it anyway)
but make sure that when we process
an event point, we only process it once
- by checking that the priority queue didn’t
return the same event point as last time

164. Can we find the same event point twice?
That is, we can discover
the same event point more than once
There are (at least) two ways to deal with this:
1. Check whether we already found the new point
- by looking it up in the priority queue
2. Don’t worry about it (INSERT it anyway)
but make sure that when we process
an event point, we only process it once
- by checking that the priority queue didn’t
return the same event point as last time
either approach gives the same time complexity

165. How do we implement the status data structure?
We need a data structure to store the status of the sweep line
i.e. the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )

166. How do we implement the status data structure?
INSERT, DELETE, FIND and PREDECESSOR/SUCCESSOR
We need a data structure to store the status of the sweep line
i.e. the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
The operations we need are

167. How do we implement the status data structure?
INSERT, DELETE, FIND and PREDECESSOR/SUCCESSOR
We need a data structure to store the status of the sweep line
i.e. the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
The operations we need are
this is the PREDECESSOR of this

168. How do we implement the status data structure?
INSERT, DELETE, FIND and PREDECESSOR/SUCCESSOR
We need a data structure to store the status of the sweep line
i.e. the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
we also need SWAP but this can be done using
INSERT and DELETE
The operations we need are
this is the PREDECESSOR of this

169. How do we implement the status data structure?
INSERT, DELETE, FIND and PREDECESSOR/SUCCESSOR
We need a data structure to store the status of the sweep line
i.e. the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
The operations we need are

170. How do we implement the status data structure?
INSERT, DELETE, FIND and PREDECESSOR/SUCCESSOR
We need a data structure to store the status of the sweep line
i.e. the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
The operations we need are
We will use a self-balancing tree (e.g. a 2-3-4 tree) as the status data structure

171. How do we implement the status data structure?
INSERT, DELETE, FIND and PREDECESSOR/SUCCESSOR
We need a data structure to store the status of the sweep line
i.e. the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
The operations we need are
We will use a self-balancing tree (e.g. a 2-3-4 tree) as the status data structure
which supports these operations in O(log n) time

172. How do we implement the status data structure?
INSERT, DELETE, FIND and PREDECESSOR/SUCCESSOR
We need a data structure to store the status of the sweep line
i.e. the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
The operations we need are
We will use a self-balancing tree (e.g. a 2-3-4 tree) as the status data structure
which supports these operations in O(log n) time
however, we need to be careful about the keys

173. How do we implement the status data structure?
We need a data structure to store the status of the sweep line
i.e. the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )

174. How do we implement the status data structure?
We need a data structure to store the status of the sweep line
i.e. the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
We insert each line segment si into the self-balancing search tree using
the description of si (i.e. its end points) as the key

175. How do we implement the status data structure?
We need a data structure to store the status of the sweep line
i.e. the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
We insert each line segment si into the self-balancing search tree using
the description of si (i.e. its end points) as the key
This may seem odd as we normally think of a key as being an integer

176. How do we implement the status data structure?
We need a data structure to store the status of the sweep line
i.e. the set of line segments which currently intersect the sweep line
ordered from left to right by where they intersect
(i.e. in the order given by the )
We insert each line segment si into the self-balancing search tree using
the description of si (i.e. its end points) as the key
This may seem odd as we normally think of a key as being an integer
Actually, all we require is that the keys have an order
and we can compare two keys in O(1) time

177. Time Complexity (sketch)
The algorithm moves the sweep line O(n + k) times,
once for each event point

178. Time Complexity (sketch)
The algorithm moves the sweep line O(n + k) times,
once for each event point
If the status data structure and priority queue structures
are implemented so that their operations take O(log n) time
(e.g. with a self-balancing tree and a binary heap, respectively)

179. Time Complexity (sketch)
The algorithm moves the sweep line O(n + k) times,
once for each event point
If the status data structure and priority queue structures
are implemented so that their operations take O(log n) time
The overall complexity then becomes O(n log n + k log n)
as claimed
(e.g. with a self-balancing tree and a binary heap, respectively)

180. Time Complexity (sketch)
The algorithm moves the sweep line O(n + k) times,
once for each event point
If the status data structure and priority queue structures
are implemented so that their operations take O(log n) time
The overall complexity then becomes O(n log n + k log n)
as claimed
This is because we do a O(n + k) operations on each data structure
while moving the sweep line
(e.g. with a self-balancing tree and a binary heap, respectively)

181. Summary
We have seen an algorithm for line segment intersection
which runs in O(n log n + k log n) time
where n is the number of line segments and k is the number of intersections
The efficiency relies on using
a Self-balancing search tree
a Binary Heap
and
We put quite a few restrictions on the input,
fixing these is fiddly but not difficult
In the original paper, they suggest adding random noise to the points
to avoid the restrictions
the approach is to move a horizontal line through the plane
which jumps between all the interesting positions

182. Dealing with the restrictions
All of these restrictions can be removed making the algorithm slightly more involved
In the interest of simplicity, we didn’t allow the input to contain any of the following:
three (or more)
which intersect at
the same point
horizontal line segments
two end points
with the same y-coordinate
lines segments
overlapping
line segments
(merge these then postprocess)
(preprocess these)
(split ties using the x-coordinate)
(swap becomes reverse)
(hints are given for the interested)