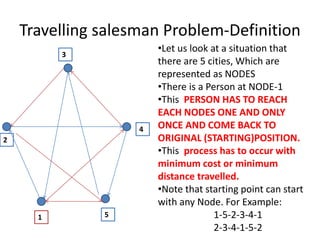
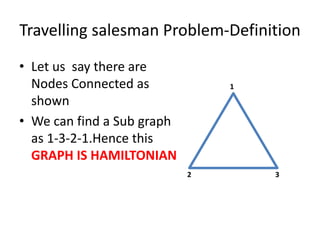
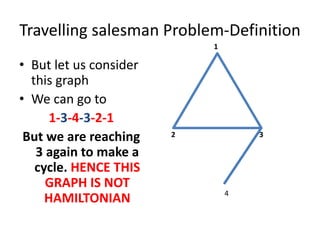
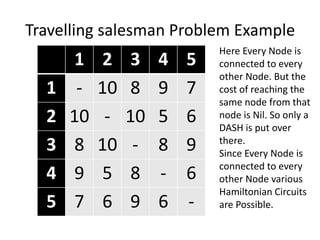
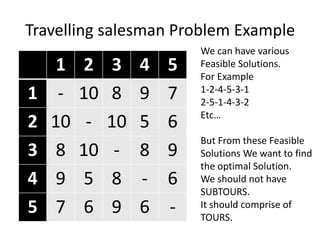
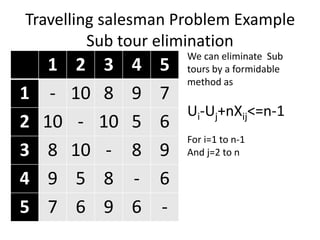
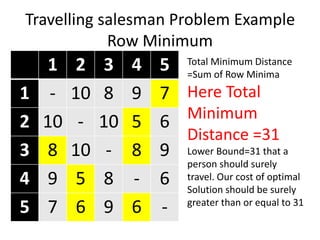
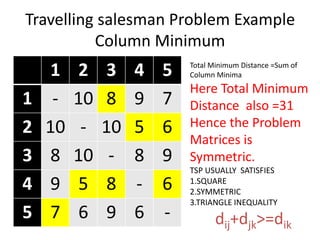
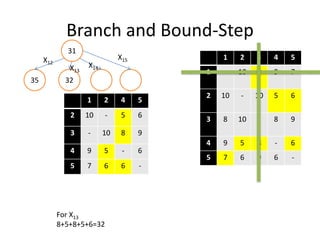
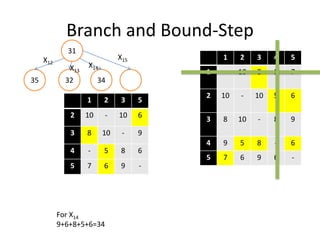
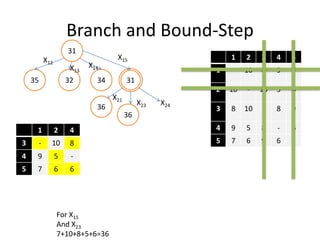
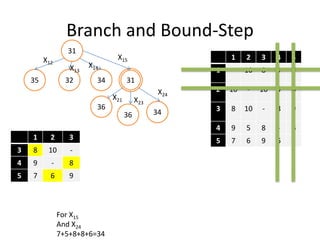
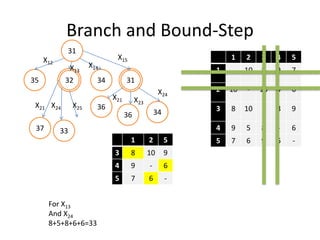
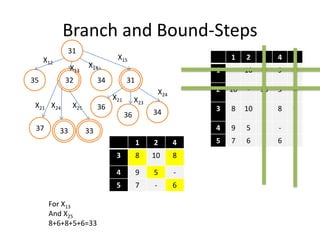
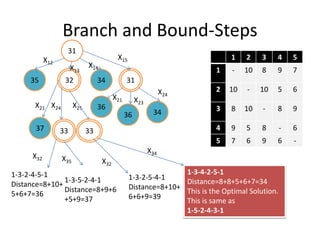
The document discusses the Travelling Salesman Problem (TSP). TSP aims to find the shortest possible route for a salesman to visit each city in a list only once and return to the origin city. It describes the problem as finding the optimal or least cost Hamiltonian circuit in a graph where cities are nodes and distances between cities are edge costs. The document provides an example problem with 5 cities, calculates possible routes and costs, and illustrates the branch and bound algorithm to solve TSP by systematically eliminating suboptimal routes until the optimal route is found.

1. Travelling Salesman Problem

2. Travelling salesman Problem-Definition
3
1
2
4
5
•Let us look at a situation that
there are 5 cities, Which are
represented as NODES
•There is a Person at NODE-1
•This PERSON HAS TO REACH
EACH NODES ONE AND ONLY
ONCE AND COME BACK TO
ORIGINAL (STARTING)POSITION.
•This process has to occur with
minimum cost or minimum
distance travelled.
•Note that starting point can start
with any Node. For Example:
1-5-2-3-4-1
2-3-4-1-5-2

3. Travelling salesman Problem-Definition
• If there are ‘n’ nodes there are (n-1)! Feasible
solutions
• From these (n-1)! Feasible solutions we have
to find OPTIMAL SOLUTION.
• This can be related to GRAPH THEORY.
• Graph is a collection of Nodes and
Arcs(Edges).

4. Travelling salesman Problem-Definition
• Let us say there are
Nodes Connected as
shown
• We can find a Sub graph
as 1-3-2-1.Hence this
GRAPH IS HAMILTONIAN
1
2 3

5. Travelling salesman Problem-Definition
• But let us consider
this graph
• We can go to
1-3-4-3-2-1
But we are reaching
3 again to make a
cycle. HENCE THIS
GRAPH IS NOT
HAMILTONIAN
1
2 3
4

6. HAMILTONIAN GRAPHS
• The Given Graph is
Hamiltonian
• If a graph is
Hamiltonian, it may
have more than one
Hamiltonian Circuits.
• For eg:
1-4-2-3-1
1-2-3-4-1 etc.,
4
1
2
3

7. Hamiltonian Graphs And Travelling
Salesman Problem
• Graphs Which are
Completely Connected i.e.,
if we have Graphs with
every vertex connected to
every other vertex, then
Clearly That graph is
HAMILTONIAN.
• So Travelling Salesman
Problem is nothing but
finding out LEAST COST
HAMILTONIAN CIRCUIT

8. Travelling salesman Problem Example
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
Here Every Node is
connected to every
other Node. But the
cost of reaching the
same node from that
node is Nil. So only a
DASH is put over
there.
Since Every Node is
connected to every
other Node various
Hamiltonian Circuits
are Possible.

9. Travelling salesman Problem Example
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
We can have various
Feasible Solutions.
For Example
1-2-4-5-3-1
2-5-1-4-3-2
Etc…
But From these Feasible
Solutions We want to find
the optimal Solution.
We should not have
SUBTOURS.
It should comprise of
TOURS.

10. Travelling salesman Problem Example-
Formulations
• Xij = 1,if person moves IMMEDIATELY from I to j.
• Objective Function is to minimize the total
distance travelled which is given by
∑∑Cij Xij
Where Cij is given by Cost incurred or Distance
Travelled
For j=1 to n, ∑ Xij=1, ɏ i
For i= 1 to n, ∑ Xij=1, ɏj
Xij=0 or 1

11. Sub Tour Elimination Constraints
• We can have Sub tours of length n-1
• We eliminate sub tour of length 1 By making Cost to travel from j to
j as infinity.
Cjj=∞
• To eliminate Sub tour of Length 2 we have
Xij+Xji<=1
• To eliminate Sub tour of Length 3 we have
Xij+Xjk+Xki<=2
• If there are n nodes Then we have the following constraints
• nc2 for length 2
• nc3 for length 3
• ……
• ncn-1 for length n-1

12. Travelling salesman Problem Example
Sub tour elimination
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
We can eliminate Sub
tours by a formidable
method as
Ui-Uj+nXij<=n-1
For i=1 to n-1
And j=2 to n

13. TSP - SOLUTIONS
• Branch and Bound Algorithm
• Heuristic Techniques

14. Travelling salesman Problem Example
Row Minimum
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
Total Minimum Distance
=Sum of Row Minima
Here Total
Minimum
Distance =31
Lower Bound=31 that a
person should surely
travel. Our cost of optimal
Solution should be surely
greater than or equal to 31

15. Travelling salesman Problem Example
Column Minimum
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
Total Minimum Distance =Sum of
Column Minima
Here Total Minimum
Distance also =31
Hence the Problem
Matrices is
Symmetric.
TSP USUALLY SATISFIES
1.SQUARE
2.SYMMETRIC
3.TRIANGLE INEQUALITY
dij+djk>=dik

16. Branch and Bound-Step
31
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
35
X12
X13
X14
X15
For X12
10+5+8+6+6=35
1 3 4 5
2 - 10 5 6
3 8 - 8 9
4 9 8 - 6
5 7 9 6 -

17. Branch and Bound-Step
31
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
35 32
X12
X13
X14
X15
For X13
8+5+8+5+6=32
1 2 4 5
2 10 - 5 6
3 - 10 8 9
4 9 5 - 6
5 7 6 6 -

18. Branch and Bound-Step
31
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
35 32 34
X12
X13
X14
X15
For X14
9+6+8+5+6=34
1 2 3 5
2 10 - 10 6
3 8 10 - 9
4 - 5 8 6
5 7 6 9 -

19. Branch and Bound-Step
31
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
35 32 34 31
X12
X13
X14
X15
For X15
7+5+8+5+6=31
1 2 3 4
2 10 - 10 5
3 8 10 - 8
4 9 5 8 -
5 - 6 9 6

20. Branch and Bound-Step
31
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
35 32 34 31
X12
X13
X14
X15
X21
X23
X24
2 3 4
3 10 - 8
4 5 8 -
5 - 9 6
For X15
And X21
7+10+8+5+6=36
36

21. Branch and Bound-Step
31
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
35 32 34 31
X12
X13
X14
X15
X21
X23 X24
For X15
And X23
7+10+8+5+6=36
36
1 2 4
3 - 10 8
4 9 5 -
5 7 6 6
36

22. Branch and Bound-Step
31
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
35 32 34 31
X12
X13
X14
X15
X21 X23
X24
For X15
And X24
7+5+8+8+6=34
36
1 2 3
3 8 10 -
4 9 - 8
5 7 6 9
36 34

23. Branch and Bound-Step
31
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
35 32 34 31
X12
X13
X14
X15
X21 X23
X24
36
36 34
X21 X24 X25
37
2 4 5
3 - 8 9
4 5 - 6
5 6 6 -
For X13
And X21
8+10+8+5+6=37

24. Branch and Bound-Step
31
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
35 32 34 31
X12
X13
X14
X15
X21 X23
X24
36
36 34
X21 X24 X25
37
For X13
And X24
8+5+8+6+6=33
1 2 5
3 8 10 9
4 9 - 6
5 7 6 -
33

25. Branch and Bound-Steps
31
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
35 32 34 31
X12
X13
X14
X15
X21 X23
X24
36
36 34
X21 X24 X25
37
For X13
And X25
8+6+8+5+6=33
33
1 2 4
3 8 10 8
4 9 5 -
5 7 - 6
33

26. Branch and Bound-Steps
31
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
35 32 34 31
X12
X13
X14
X15
X21 X23
X24
36
36 34
X21 X24 X25
37 33 33
X32 X35
1-3-2-4-5-1
Distance=8+10+
5+6+7=36
1-3-5-2-4-1
Distance=8+9+6
+5+9=37

27. Branch and Bound-Steps
31
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
35 32 34 31
X12
X13
X14
X15
X21 X23
X24
36
36 34
X21 X24 X25
37 33 33
X32 X35
1-3-2-4-5-1
Distance=8+10+
5+6+7=36
1-3-5-2-4-1
Distance=8+9+6
+5+9=37
X32
X34
1-3-2-5-4-1
Distance=8+10+
6+6+9=39
1-3-4-2-5-1
Distance=8+8+5+6+
7=34

28. Branch and Bound-Steps
31
1 2 3 4 5
1 - 10 8 9 7
2 10 - 10 5 6
3 8 10 - 8 9
4 9 5 8 - 6
5 7 6 9 6 -
35 32 34 31
X12
X13
X14
X15
X21 X23
X24
36
36 34
X21 X24 X25
37 33 33
X32 X35
1-3-2-4-5-1
Distance=8+10+
5+6+7=36
1-3-5-2-4-1
Distance=8+9+6
+5+9=37
X32
X34
1-3-2-5-4-1
Distance=8+10+
6+6+9=39
1-3-4-2-5-1
Distance=8+8+5+6+7=34
This is the Optimal Solution.
This is same as
1-5-2-4-3-1