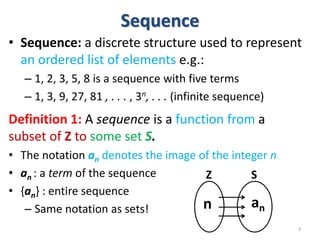
The document discusses sequences and summations. It provides examples and definitions of different types of sequences such as arithmetic and geometric sequences. It also discusses recurrence relations, which express a term in a sequence based on prior terms. Examples are provided to demonstrate finding terms of sequences given a recurrence relation. The document is a lecture on discrete mathematics concepts related to sequences.

1. Discrete Structures
Sequences and Summations
Dr. Muhammad Humayoun
Assistant Professor
COMSATS Institute of Computer Science, Lahore.
mhumayoun@ciitlahore.edu.pk
https://sites.google.com/a/ciitlahore.edu.pk/dstruct/
A lot of material is taken from the slides of Dr. Atif and Dr. Mudassir
1

2. 2

3. Sequence
• Sequence: a discrete structure used to represent
an ordered list of elements e.g.:
– 1, 2, 3, 5, 8 is a sequence with five terms
– 1, 3, 9, 27, 81 , . . . , 3n, . . . (infinite sequence)
Definition 1: A sequence is a function from a
subset of Z to some set S.
• The notation an denotes the image of the integer n
• an : a term of the sequence
• {an} : entire sequence
– Same notation as sets!
3
Z S
n an

4. Length of Sequence:
A sequence may be Finite or Infinite.
4

5. Sequences and Rules
5

6. Naming Sequences
6

7. Examples 1
at Page# 156
• Consider the sequence {an}, where an = 1/n.
The list of the terms of this sequence beginning with a1:
a1, a2, a3, a4, …
{1, 1/2, 1/3, 1/4 , … }
• Consider the sequence {an}, where an = 3n.
The list of the terms of this sequence beginning with a1:
{3, 6, 9, 12 , …}
• The Sequence {bn}, where bn=2n
The list of the terms of this sequence beginning with b1:
{2, 4, 8, 16, … }
7

8. Example 3
at Page# 157
• Is the sequence {sn} with sn = −1 + 4n an arithmetic
progressions with initial terms -1 and common
differences equal to 4? if we start at n = 0. The list of
terms s0 , s1 , s2 , s3 , . . . begins with −1, 3, 7, 11, . . . ,
Yes, it is arithmetic progression.
• Is the sequence {tn} with tn = 7 − 3n an arithmetic
progressions with initial terms 7 and common
differences equal to -3? if we start at n = 0. the list of
terms t0 , t1 , t2 , t3 , . . . begins with 7, 4, 1,−2, . . . .
 Yes, it is arithmetic progression.
8

9. Types of Sequence
• Arithmetic Sequence
Next term is calculated by adding in the preceding term.
• Geometric Sequence
 Next term is calculated by multiplying by the preceding term.
Arithmetic Series
 Sum of Arithmetic Sequences
Geometric Series
 Sum of Geometric Sequences
9

10. • Next class
10

11. Types of Sequence and Series
11

12. Arithmetic Progression/ Sequences
12

13. Arithmetic Progression/ Sequences
(Conti…)
13

14. Sequences and Summations
14

15. Sequences and Summations
Arithmetic Progressions
15

16. Sequences and Summations
Arithmetic Progressions
16

17. Sequences and Summations
Arithmetic Progressions
17

18. Arithmetic Progressions
18

19. Arithmetic Progressions
19

20. Arithmetic Progressions
20

21. Arithmetic Progressions
21

22. General form of an Arithmetic Sequence
22

23. 23

24. 24

25. 25

26. 26

27. 27

28. 28

29. 29

30. 30

31. Geometric Progression
• A geometric progression is a sequence of the form
a, ar1, ar2, . . . , arn-1, . . .
where
the initial term a
and the common ratio r are real numbers.
• A geometric progression is a discrete analogue of
the exponential function f (x) = arx.
• Geometric Progression: an = ar n-1
 ar0, ar1, ar2, ar3, …
• Is the sequence {bn} Geometric Progression???
31

32. Example# 2
at Page 157
• Is the sequence {bn} with bn = (−1)n a geometric progression with
initial term 1 and common ratio −1? if we start at n = 0. the list of
terms b0 , b1 , b2 , b3 , b4 , . . . begins with 1,−1, 1,−1, 1, . . .
 Yes, it is Geometric Progression.
• Is the sequence {cn} with cn = 2 ・ 5n a geometric progression
with initial term 2 and common ratio 5? if we start at n = 0. the
list of the terms c0 , c1 , c2 , c3 , c4 , . . . begins with 2, 10, 50, 250,
1250, . . .
 Yes, it is Geometric Progression.
• Is the sequence {dn} with dn = 6 ・ (1/3)n a geometric progression
with initial term 6 and common ratio 1/3? if we start at n = 0. the list
of the terms d0 , d1 , d2 , d3 , d4 , . . . begins with 6, 2, 2/3, 2/9,
2/27,...
 Yes, it is Geometric Progression.
32

33. Strings
• Finite Sequences of the form a1, a2, . . . , an are
called strings.
• The length of a string is the number of terms in
the string.
• EXAMPLE 4 at Page# 157, The string abcd is a
string of length four.
• The empty string, denoted by λ, is the string that
has no terms. The empty string has length zero.
33

34. Recurrence Relations
A recurrence relation for the sequence {an} is an
equation that expresses an in terms of one or more
of the previous terms of the sequence.
A sequence is called a solution of a recurrence
relation if its terms satisfy the recurrence relation.
(A recurrence relation is said to recursively define a
sequence.)
34

35. Example 5 at Page# 158
Let {an} be a sequence that satisfies the recurrence
relation an = an−1 + 3 for n = 1, 2, 3, ...
Suppose that a0 = 2. What are a1, a2, and a3?
• a1 = a0 + 3 = 5
• a2 = a1 + 3 = 8
• a3 = a2 + 3 = 11
{5, 8, 11, …}
35

36. Example 6 at Page# 158
Let {an} be a sequence that satisfies the recurrence
relation an = an-1 − an-2 for n = 2, 3, 4, . . . , Suppose
that a0 = 3 and a1 = 5 . What are a2, and a3?
• an = an-1 − an-2
• a2 = a2-1 − a2-2 a2 = a1 − a0
• a2 = a1 − a0 a2 = 5 − 3= 2
• a3 = a2 − a1 a3 = 2 − 5= -3
{2,-3, …}
36

37. Fibonacci sequence
EXAMPLE 7 at Page# 158
• The Fibonacci sequence, f0 , f1 , f2 , . . . , is defined by
the initial conditions f0 = 0, f1 = 1, and the recurrence
relation fn = fn−1 + fn−2 for n = 2, 3, 4, . . .
• Find the Fibonacci numbers f2 , f3 , f4 , f5 ,and f6?
• fn = fn−1 + fn−2
• f2 = f2−1 + f2−2 f2 = f1 + f0 f2 = 1 + 0 f2 = 1
• f3 = f3−1 + f3−2 f3 = f2 + f1 f3 = 1 + 1 f3 = 2
• f4 = f4−1 + f4−2 f4 = f3 + f2 f4 = 2 + 1 f4 = 3
• f5 = f5−1 + f5−2 f5 = f4 + f3 f5 = 3 + 2 f5 = 5
• f6 = f6−1 + f6−2 f6 = f5 + f4 f6 = 5 + 3 f6 = 8
37

38. EXAMPLE 8 at Page# 159
• Suppose that {an} is the sequence of integers defined by an = n!,
the value of the factorial function at the integer n, where n = 1, 2,
3, . . .. Because n! = n((n − 1)(n − 2) . . . 2 ・ 1) = n(n − 1)! = nan−1,
we see that the sequence of factorials satisfies the recurrence
relation an = nan−1, together with the initial condition a1 =1.
38

39. Example 9
at Page#159
• Determine whether the sequence {an}, where an
= 3n for every nonnegative integer n, is a solution
of the recurrence relation an = 2an−1 − an−2 for n =
2, 3, 4, . . . .
• Solution
For n  2 we see that
2an-1 – an-2 = 2(3(n – 1)) – 3(n – 2) = 3n = an.
Therefore, {an} with an=3n is a solution of the
recurrence relation.
39

40. Example 9
at Page#159
• Determine whether the sequence {an}, where an
= 2n for every nonnegative integer n, is a solution
of the recurrence relation an = 2an−1 − an−2 for n =
2, 3, 4, . . . . Answer the same question where an
= 2n
•For n  2 we see that
2an-1 – an-2 = 2(2(n – 1)) – 2(n – 2) = 2n = an.
•Therefore, {an} with an=2n is a solution of the
recurrence relation.
40

41. Example 9
at Page#159
• Determine whether the sequence {an}, where an =
3n for every nonnegative integer n, is a solution of
the recurrence relation an = 2an−1 − an−2 for n = 2, 3,
4, . . . . Answer the same question where an = 2n
• For n  2 we see that
• Note that a0 = 1, a1 = 2, and a2 = 4.
• Because 2a1 − a0 = 2 ・ 2 − 1 = 3 ≠ a2
•Therefore, {an} with an= 2n is not a solution of the
recurrence relation.
41

42. Example 9
at Page#159
• Determine whether the sequence {an}, where an
= 3n for every nonnegative integer n, is a solution
of the recurrence relation an = 2an−1 − an−2 for n =
2, 3, 4, . . . . Answer the same question where an
= 5
•For n  2 we see that
2an-1 – an-2 = 2(5) – 5 = 5 = an.
•Therefore, {an} with an=5 is a solution of the
recurrence relation.
42

43. Example 10 at Page# 159
Not Included
Solve the recurrence relation and initial condition in Example 5.
Let {an} be a sequence that satisfies the recurrence relation an = an−1 + 3 for n =
1, 2, 3, ... Suppose that a0 = 2. What are a1, a2, and a3?
• a1 = a0 + 3 = 5 a1 = 2 + 3 = 5 a1 = 2 + 3 = 2 + 3 .1
• a2 = a1 + 3 = 8 a2 = 5 + 3 = 8 a2 = (2 + 3 ) + 3 = 2+3.2
• a3 = a2 + 3 = 11 a3 = 8 + 3 = 11 a3 = [(2 + 3 ) + 3] + 3 = 2+3.3
• ...
• an = an−1 + 3 = 2 + 3(n − 1).
43

44. 44

45. Determining the Sequence formula
• 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, …
– The sequence alternates 1’s and 0’s, increasing the
number of 1 and 0 each time.
• 1, 2, 2, 3, 4, 4, 5, 6, 6, 7, 8, 8, …
– The sequence increases by one but repeats all even
numbers twice.
• 1, 0, 2, 0, 4, 0, 8, 0, 16, 0, …
– The non-zero numbers are geometric sequences (2n),
such that every non-zero number is succeeded by a
zero.
45

46. Determining the Sequence formula
• 3, 6, 12, 24, 48, 96, 192, …
Each term is twice the previous
a1 = 3, an = 2*an-1 (recurrence relation)
• Is the above a Geometric Sequence? (an = arn-1)?
an = 3 * 2n-1 (sequence formula)
• 15, 8, 1, -6, -13, -20, -27, ….
Each term is 7 less than previous term
a1 = 15, an = an-1 - 7
an = 22 – 7*n
46

47. Example 12
at Page# 161
• Find formulae for the sequences with the following first five terms:
• (a) 1, 1/2, 1/4, 1/8, 1/16
• Solution:
 The sequence with an = (½)n, n = 0, 1, 2, . . . is a possible match. It is a
geometric progression with
 a = 1 and r = 1/2.
• (b) 1, 3, 5, 7, 9
• Solution:
 We note that each term is obtained by adding 2 to the previous term. The
sequence with an = 2n + 1, n = 0, 1, 2, . . . is a possible match. It is a
Arithmetic progression with
 a = 1 and d = 2.
47

48. Example 12
at Page# 161
• (c) 1, −1, 1, −1, 1.
• Solution:
The terms alternate between 1 and −1. The sequence
with an = (−1)n, n = 0, 1, 2 . . . is a possible match. It is
a geometric progression with
a =1 and r = −1.
48

49. Example 13
at Page# 161
• How can we produce the terms of a sequence if
the first 10 terms are 1, 2, 2, 3, 3, 3, 4, 4, 4, 4?
• Solution:
A rule for generating this sequence is that the integer
n appears exactly n times.
49

50. Example 14
at Page# 161
• How can we produce the terms of a sequence if
the first 10 terms are 5, 11, 17, 23, 29, 35, 41, 47,
53, 59?
• Solution:
A rule for generating this sequence is 5+6n
It is an arithmetic progression with a = 5 and d = 6.
50

51. Example 15
at Page# 161
• How can we produce the terms of a sequence if the
first 10 terms are 1, 3, 4, 7, 11, 18, 29, 47, 76, 123?
• Solution:
• We guess that the sequence is determined by the
recurrence relation
Ln = Ln−1 + Ln−2 with initial conditions L1 = 1 and L2 = 3
• Note:
It is a Same recurrence relation as the Fibonacci
sequence, but with different initial conditions). This
sequence is known as the Lucas sequence.
51

52. Example 16
at Page# 161
• Conjecture a simple formula for an if the first 10
terms of the sequence {an} are 1, 7, 25, 79, 241,
727, 2185, 6559, 19681, 59047.
• Solution:
We see that an = 3n − 2 for 1 ≤ n ≤ 10 and conjecture
that this formula holds for all n.
52

53. Some Useful Sequences
n(n+1)/2 : 1, 3, 6, 10, 15, …
53

54. Determining the Sequence formula
• 3, 5, 8, 12, 17, 23, 30, 38, 47, ….
– Initial condition: a1 = 3
– a2 = 5, a3 = 8, a4 = 12
– a2 = a1 + 2
– a3 = a2 + 3
– a4 = a3 + 4
– ….
– an = an-1 + n
– The difference between successive terms increased
by 1
54

55. Determining the Sequence formula
55
See Examples 1 to 16 on pages 156 - 162

56. Summations
• The sum of the terms am , am+1 , . . . , an from the
sequence {an}is:
am+ am+1+ . . . +an
denoted by or
Where,
 denotes Summation
j is the index of summation
m is lower limit
n is upper limit
56


n
m
j
j
a

57. Sequences and Summations
57

58. 58

59. EXAMPLE 17
at Page# 163
• Use summation notation to express the sum of
the first 100 terms of the sequence {aj }, where
aj = 1/j for j = 1, 2, 3, . . . .
• Solution:
59

60. Example 18
at Page# 164
• What is the value of ?
60

61. Example 19
at Page# 164
61
What is the value of ?

62. Example 20
at Page# 164
What is value of by shifting Index of summation ?
Note: We want the index of summation to run between 0 to 4
rather than from 1 to 5.
• Let , k= j-1 (for shifting indexes of summations)
• then by putting the values of limits
for j=1, k=j-1 k=1-1=0
for j=5, k=j-1 k=5-1=4
• By putting the value of j2, we have if k=j-,1 then j=k+1
becomes
By shifting k to j, we have
• = (0+1)2+ (1+1)2+ (2+1)2+ (3+1)2+ (4+1)2 = 1+4+9+16+25=55
62

63. 63

64. 64

65. See Ex. 17-20,
22, starting
from Page
163.

66. Examples
1. Express the sum of first 100 terms of the sequence
{𝑎𝑛} where 𝑎𝑛 =
1
𝑛
for n=1, 2, 3, ….
2. What is the value of 𝑗=1
5
𝑗2
3. What is the value of 𝑘=4
8
−1 𝑘
66

67. 67

68. Example 21
at Page# 165
• Evaluate the following double Summation
68
=6(1)+ 6(2)+ 6(3)+6(4)
=6+12+18+24
= 60

69. Example 22
at Page# 165
• What is the value of ?
• Solution:
• represents the sum of the values of s
for all the members of the set {0, 2, 4}, it follows
that
= 0+2+4= 6
69

70. Example 23 at Page# 166
70
Find

71. 71

72. Exercise
at page#167
72

73. Exercise
at page#167
73

74. Exercise
at page#167
74

75. Exercise
at page#167
75

76. Exercise
at page#167
76
2, 5, 8, 11, 14, 17, 20, 23, 26, 29.

77. Exercise
at page#167
77

78. Exercise
at page#167
78
2,4,6,10,16,26,42,68,110,178

79. Exercise
at page#167
79

80. Exercise
at page#167
80

81. Exercise
at page#167
81

82. Exercise
at page#167
82

83. Exercise
at page#167
83

84. Exercise
at page#167
84

85. Exercise
at page#167
85

86. Exercise
at page#167
86

87. Exercise
at page#167
• 1, 2, 4, 7, 11, 16, 22, ....
• 1, 2, 4, 1, 2, 4, 1, 2, 4, ....
• 1, 2, 4, 8, 16, 32
87