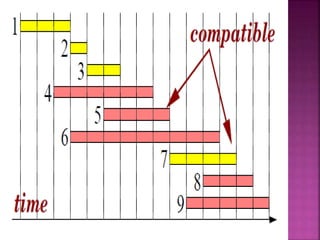
A greedy algorithm is a problem-solving technique that follows the problem-solving heuristic of making locally optimal choices at each step to find a global optimum. While this may find an optimal solution, it does not guarantee to do so as it does not consider the overall problem. The document discusses applying a greedy algorithm to solve the activity selection problem by always selecting the next activity that finishes earliest without conflicting with previously selected activities. It provides recursive and iterative implementations of the greedy algorithm to solve this problem in O(n log n) time by first sorting activities by finish time.

2. PREPARED BY:
Qurat Ul Ain
SUBMITTED TO:
Ma’am Samreen

4.  A greedy algorithm is a mathematical process
that looks for simple, easy-to-implement
solutions to complex, multi-step problems by
deciding which next step will provide the
most obvious benefit.
 Such algorithms are called greedy because
while the optimal solution to each smaller
instance will provide an immediate output,
the algorithm doesn’t consider the larger
problem as a whole. Once a decision has
been made, it is never reconsidered.

5.  Greedy algorithms work by recursively
constructing a set of objects from the
smallest possible constituent parts.
 RECURSION is an approach to problem
solving in which the solution to a particular
problem depends on solutions to smaller
instances of the same problem.
 The advantage to using a greedy algorithm is
that solutions to smaller instances of the
problem can be straightforward and easy to
understand.
 The disadvantage is that it is entirely
possible that the most optimal short-term
solutions may lead to the worst possible
long-term outcome.

6.  Each step of the Greedy algorithm must take
one of several possible choices. The greedy
strategy advocates making the choice that is
the best at the moment. It is used for solving
optimization problems.
 an optimization problem is the problem of
finding the best solution from all feasible
solutions.
 Greedy algorithms are often used in ad
hoc mobile networking to efficiently
route packets with the fewest number
of hops and the shortest delay possible. They
are also used in machine learning, business
intelligence (BI), artificial intelligence (AI)
and programming.

7.  We are given a set S of n activities S={a1, . .
. , an}
 Each activity ai has a start time si and finish
time fi, where i-th activity ai = [si, fi) starts
at time si and finishes at time fi.
Where 0<=si<=fi<= ∞
 These activities require the same resource
(for example, one lecture hall).

8. Two activities ai and aj are compatible if
the intervals [si, fi) and [sj , fj) do not
overlap, i.e they are disjoint.
 The activity-selection problem (ASP) is to
select a maximum size subset of mutually
compatible activities.

10.  Consider following set of activities,
 The subset {a3, a9, a11},
{a1, a4, a8, a11}
(a2, a4, a9, a11}
ARE COMPATIBLE ACTIVITIES.
i 1 2 3 4 5 6 7 8 9 10 11
Si 1 3 0 5 3 5 6 8 8 2 12
Fi 4 5 6 7 9 9 10 11 12 14 16

11.  Assume activities sorted in increasing order
of finish time fi
 Let c[i,j] be the number of activities in the
maximal solution for the subset Sij, i.e. the
largest number of compatible activities
starting from time fi, finishing at time sj
 Recursively
C[I,j]= { 0 if Sij=Ф }
C[I,j]= {max i<k<j c[I,k]+c[k,j]+1 otherwise }
 Then the maximum number of compatible
activities is c[0, n + 1].

12.  Greedy choice. Select an activity with
minimum fi. Remove it and incompatible
activities. Continue until no more activities
left.
This can be implemented with a recursive
algorithm:

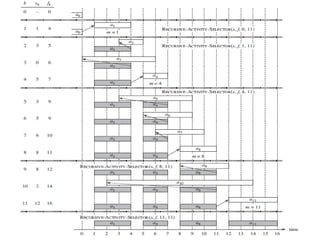
13.  Input: s[1..n] is the array of start times, f[1..n] is
the array of finish times , k is the index, n is the
total no. of activities
 RECURSIVE-ACTIVITY-SELECTOR(s, f, k, n)
// Activities are sorted by finish time.
// i is the activity selected previously. Start from k=0
1 m = k + 1
2 while m<= n and s[m] < f[k] // Find the first
activity in Sk to finish
3 m = m + 1
4 if m <=n then
5 return {am} RECURSIVE-ACTIVITY-
SELECTOR(s,f,m,n)
6 else return Ф;

14.  Line 1: Initial call: REC-ACTIVITY-
SELECTOR(s, f, 0, n). increment in m by k
(moving next position)
 Line 2-3: the while loop looks for the first
activity in Sk to finish. The loop examines all
activities until it finds first activity am that is
compatible with ak (line 4)
 Line 5: returns am activity, adding it (union)
in the set sk
 Line 6: when we have examined all activities
m>n then the loop terminates

16.  The running time of the Algorithm is:
Because over all recursive calls, each
activity is examined exactly once. So it
takes constant time Θ (n) for n activities.

17. In this algorithm the activities are sorted
according to their finishing time, from the
earliest to the latest. Then the activities are
greedily selected by going down the list and
by picking whatever activity that is
compatible with the current selection.
It collects selected activities into a set A and
returns this set when it is done.

18. GREEDY-ACTIVITY-SELECTOR (s,f)
n=s.length
2 A={a1}
3 K=1
4 For m=2 to n
5 If s[m]>=f[k]
6 A= aU{am}
7 K=m
8 Return A

19.  The procedure works as follows.
 The variable k indexes the most recent
addition to A, corresponding to the activity
ak in the recursive version. Since we
consider the activities in order of
monotonically increasing finish time, fk is
always the maximum finish time of any
activity in A.

20.  Lines 2–3 select activity a1, initialize A to contain just
this activity, and initialize k to index this activity.
 The for loop of lines 4–7 finds the earliest activity
in Sk to finish. The loop considers each activity am in
turn and adds am to A if it is compatible with all
previously selected activities; such an activity is the
earliest in Sk to finish.
 line 5 check that its start time sm is not earlier
than the finish time fk of the activity most recently
added to A.
 If activity am is compatible, then lines 6–7 add
activity am to A and set k to m.
 The set A returned by the call GREEDY-ACTIVITY-
SELECTOR ( s,f) is precisely the set returned by the
call RECURSIVE-ACTIVITY-SELECTOR(s; f; 0; n).

21.  Lines 2–3 select activity a1, initialize A to contain
just this activity, and initialize k to index this
activity.
 The for loop of lines 4–7 finds the earliest activity in
Sk to finish. The loop considers each activity am in
turn and adds am to A if it is compatible with all
previously selected activities; such an activity is the
earliest in Sk to finish.
 check (in line 5) that its start time sm is not earlier
than the finish time fk of the activity most recently
added to A.
 If activity am is compatible, then lines 6–7 add
activity am to A and set k to m. The set A returned
by the call GREEDY-ACTIVITY-SELECTOR(s,f)is
precisely the set returned by the call RECURSIVE-
ACTIVITY-SELECTOR(s,f, 0, n)

22.  The sorting part can be as
 small as O(n log n) and the
 other part is O(n), so the
 total is O(n log n).