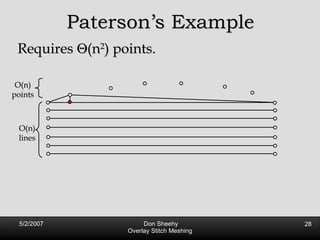
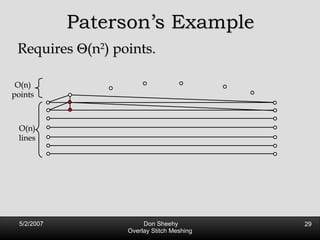
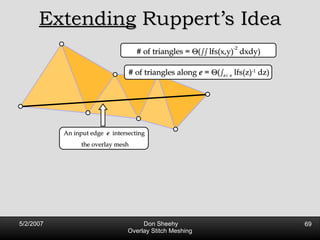
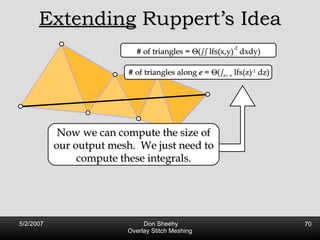
The document describes an algorithm called Overlay Stitch Meshing (OSM) for producing triangulations with no large angles from planar straight line graphs. The algorithm produces triangles with angles between 170 degrees and results in a mesh size that is O(log L/s) competitive with the optimal triangulation, where L is the total edge length and s is the minimum feature size. It works by overlaying triangles and only keeping overlay edges that intersect the input graph in a "good" way, with an angle of at least 30 degrees. The algorithm and its analysis introduce new techniques for proving logarithmic competitiveness.

1. Overlay Stitch Meshing

2. A competitive algorithm for no-large-angle triangulation Don Sheehy Joint work with Gary Miller and Todd Phillips To appear at ICALP 2007

3. The Problem Input: A Planar Straight Line Graph

4. The Problem Input: A Planar Straight Line Graph Output: A Conforming Triangulation

5. The Problem Input: A Planar Straight Line Graph Output: A Conforming Triangulation

6. Why would you want to do that?

12. What went wrong?

13. What if you don’t know the function? ? ?

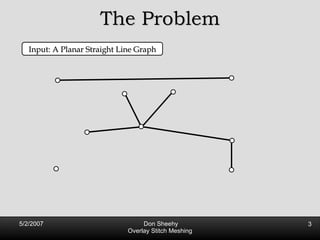
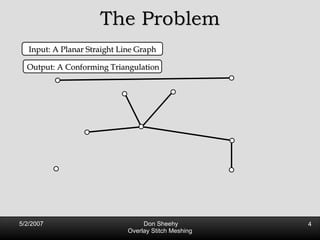
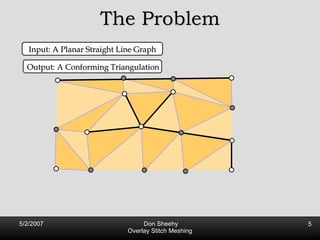
14. 2 Definitions of Quality 1. No Large Angles [Babuska, Aziz 1976]

15. 2 Definitions of Quality 1. No Large Angles [Babuska, Aziz 1976] 2. No Small Angles

16. No Small Angles

17. No Small Angles You may have heard of these before. Delaunay Refinement Sparse Voronoi Refinement Quadtree

18. Paying for the spread L s Spread = L/s

19. Paying for the spread Optimal No-Large-Angle Triangulation

20. Paying for the spread What if we don’t allow small angles?

21. Paying for the spread O(L/s) triangles! What if we don’t allow small angles?

22. Paying for the spread O(L/s) triangles! What if we don’t allow small angles? Fact: For inputs with NO edges , no-small-angle meshing algorithms produce output with O(n log L/s) size and angles between 30 o and 120 o

23. What to do? Small input angles can force even smaller ouput angles. [Shewchuk ’02]

24. No Large Angles

25. Polygons with Holes [Bern, Mitchell, Ruppert 95] – - All triangles are nonobtuse. - Output has O(n) triangles.

26. Polygons with Holes [Bern, Mitchell, Ruppert 95] – - All triangles are nonobtuse. - Output has O(n) triangles. Does not work for arbitrary PSLGs

27. Paterson’s Example Requires  (n 2 ) points. O(n) points O(n) lines

28. Paterson’s Example Requires  (n 2 ) points. O(n) points O(n) lines

29. Paterson’s Example Requires  (n 2 ) points. O(n) points O(n) lines

30. Paterson’s Example Requires  (n 2 ) points. O(n) points O(n) lines

31. Paterson’s Example Requires  (n 2 ) points. O(n) points O(n) lines

32. Paterson’s Example Requires  (n 2 ) points. O(n) points O(n) lines

33. Propagating Paths

34. Propagating Paths

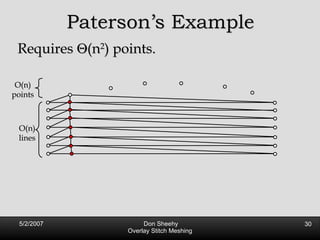
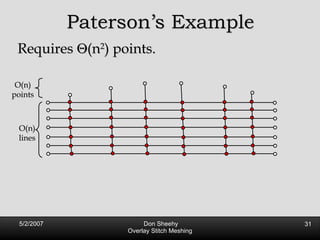
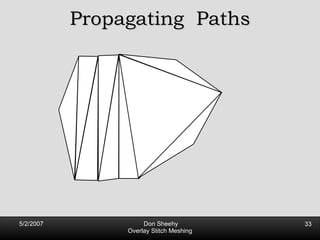
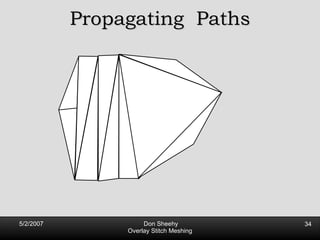
35. Propagating Paths First introduced by Mitchell [93] Later Improved by Tan [96] Worst Case Optimal Size O(n 2 ) Angle bounds: 132 o

36. The OSM Algorithm (Overlay Stitch Meshing)

37. The OSM Algorithm (Overlay Stitch Meshing) Results: Angles bounded by 170 o O(log L/s) competitive size

38. The OSM Algorithm (Overlay Stitch Meshing)

39. The OSM Algorithm (Overlay Stitch Meshing)

40. The OSM Algorithm (Overlay Stitch Meshing)

41. The OSM Algorithm (Overlay Stitch Meshing)

42. The OSM Algorithm (Overlay Stitch Meshing)

43. The OSM Algorithm (Overlay Stitch Meshing)

44. The OSM Algorithm (Overlay Stitch Meshing)

45. The OSM Algorithm (Overlay Stitch Meshing)

46. The OSM Algorithm (Overlay Stitch Meshing)

47. The OSM Algorithm (Overlay Stitch Meshing)

48. The OSM Algorithm (Overlay Stitch Meshing)

49. The OSM Algorithm (Overlay Stitch Meshing) An Overlay Edge is kept if 1. It does not intersect the input, OR 2. It forms a good intersection with the input. at least 30 o

50. Angle Guarantees

51. Angle Guarantees

52. Angle Guarantees We want to show that angles at stitch vertices are bounded by 170 o

53. Angle Guarantees An Overlay Triangle

54. Angle Guarantees An Overlay Triangle An Overlay Edge

55. Angle Guarantees An Overlay Triangle An Overlay Edge Gap Ball

56. Angle Guarantees A Good Intersection

57. Angle Guarantees A Bad Intersection

58. Angle Guarantees A Bad Intersection

59. Angle Guarantees A Bad Intersection How Bad can it be?

60. Angle Guarantees How Bad can it be? About 10 o About 170 o

61. Angle Guarantees How Bad can it be? About 10 o Theorem: If any input edge makes a good intersection with an overlay edge then any other intersection on that edge is not too bad . About 170 o

62. Size Bounds

63. Size Bounds How big is the resulting triangulation?

64. Size Bounds How big is the resulting triangulation? Goal: log(L/s)-competitive with optimal

65. Local Feature Size lfs(x) = distance to second nearest input vertex. x lfs(x) Note: lfs is defined on the whole plane before we do any meshing.

66. Ruppert’s Idea r c r =  (lfs(c)) area(  ) =  (lfs(c) 2 ) # of triangles =  ( ss 1/lfs(x,y) 2 dxdy)

67. Ruppert’s Idea r c r =  (lfs(c)) area(  ) =  (lfs(c) 2 ) # of triangles =  ( ss 1/lfs(x,y) 2 dxdy) dy dx This represents a  (dxdy/lfs(x,y) 2 ) fraction of the triangle.

68. Ruppert’s Idea r c r =  (lfs(c)) area(  ) =  (lfs(c) 2 ) # of triangles =  ( ss lfs(x,y) -2 dxdy) Caveat : Only Works for meshes with bounded smallest angle.

69. Extending Ruppert’s Idea An input edge e intersecting the overlay mesh # of triangles along e =  ( s z 2 e lfs(z) -1 dz) # of triangles =  ( ss lfs(x,y) -2 dxdy)

70. Extending Ruppert’s Idea Now we can compute the size of our output mesh. We just need to compute these integrals. # of triangles along e =  ( s z 2 e lfs(z) -1 dz) # of triangles =  ( ss lfs(x,y) -2 dxdy)

71. Output Size Stitch Vertices Added =  ( s z 2 E lfs(z) -1 dz) Overlay Mesh Size =  ( ss lfs(x,y) -2 dxdy) O(n log L/s) O(log L/s) £ |OPT| We’ll Prove this now

72. What can we say about the optimal no-large-angle triangulation?

73. Competitive Analysis Warm-up 90 o

74. Competitive Analysis Warm-up ? o

75. Competitive Analysis Warm-up

76. Competitive Analysis Warm-up

77. Competitive Analysis Warm-up Suppose we have a triangulation with all angles at least 170 o . the optimal

78. Competitive Analysis Warm-up Suppose we have a triangulation with all angles at least 170 o . the optimal Every input edge is covered by empty lenses.

79. Competitive Analysis This is what we have to integrate over. We show that in each lens, we put O(log (L/s)) points on the edge. In other words: s e’ 1/lfs(z) dz = O(log (L/s)) e’

80. Competitive Analysis e’ s z 2 e’ 1/lfs(z) dz = O(log (L/s))

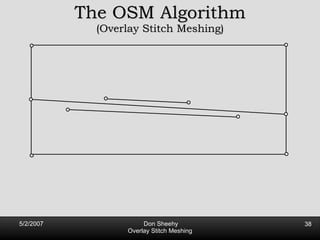
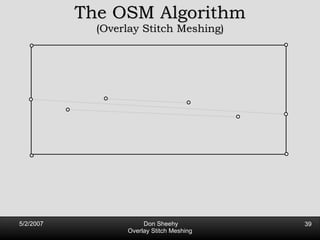
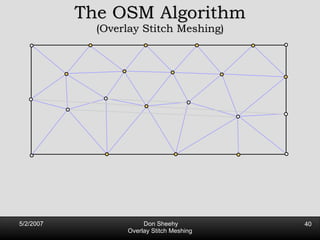
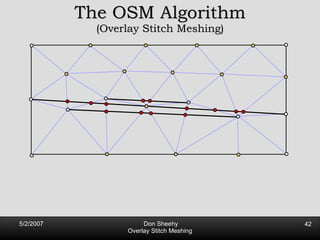
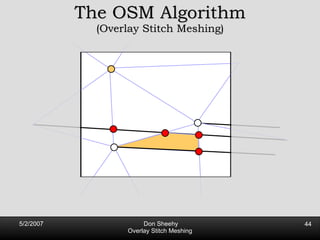
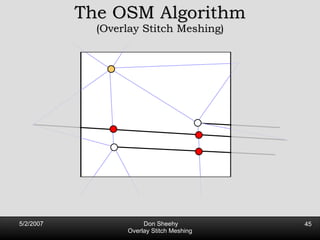
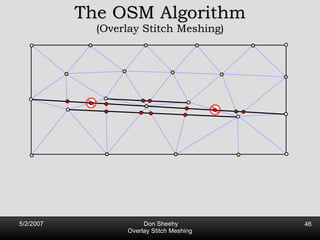
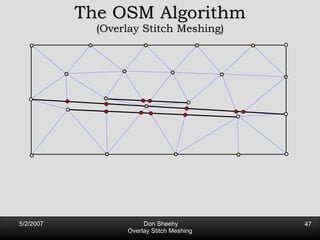
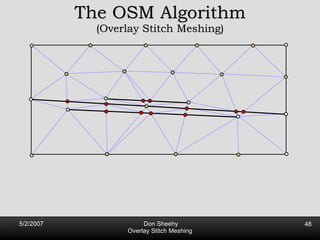
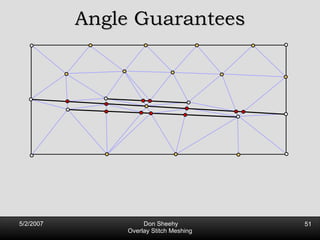
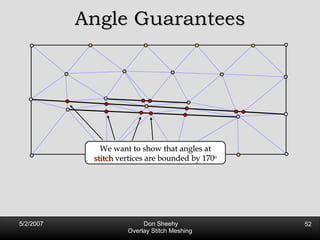
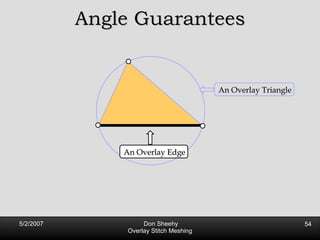
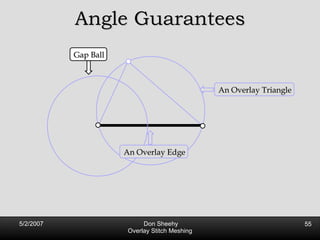
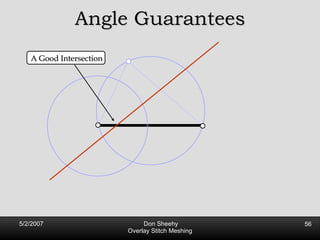
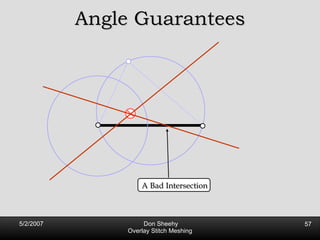
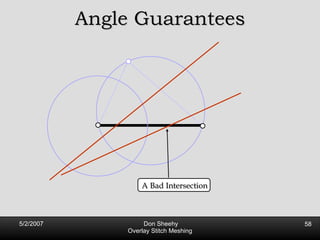
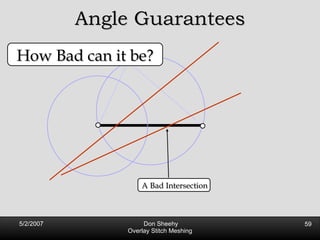
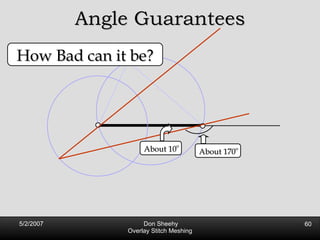
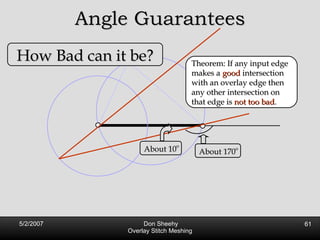
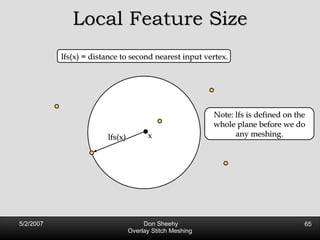
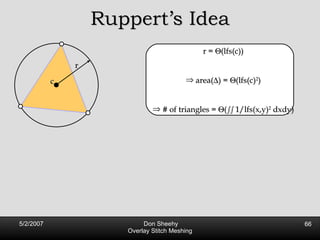
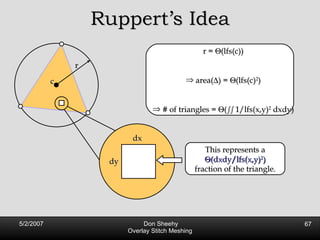
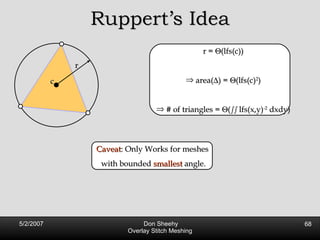
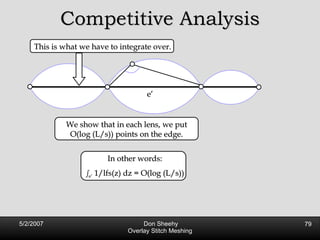
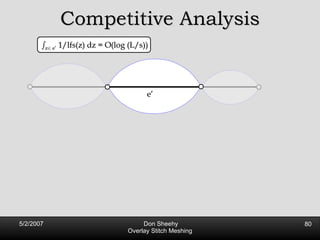
81. Competitive Analysis s z 2 e’ 1/lfs(z) dz = O(log (L/s)) e’ 1 st trick: lfs ¸ s everywhere 2 nd trick: lfs ¸ ct for t 2 [0, l /2] t s z 2 e’ 1/lfs(z) dz · 2 s 0 s 1/s + 2 s s l /2 1/x dx = O(1) + O(log l /s) = O(log L/s) Parametrize e’ as [0, l ]

82. Conclusions

83. Conclusion A new algorithm for no-large-angle triangulation. The output has bounded degree triangles. The first log-competitive analysis for such an algorithm. We used some of the high school calculus you thought you forgot.

84. Where to go from here? 3D? Better angle bounds? Leverage lower bound technology for constant competitive algorithm.

85. Thank you.