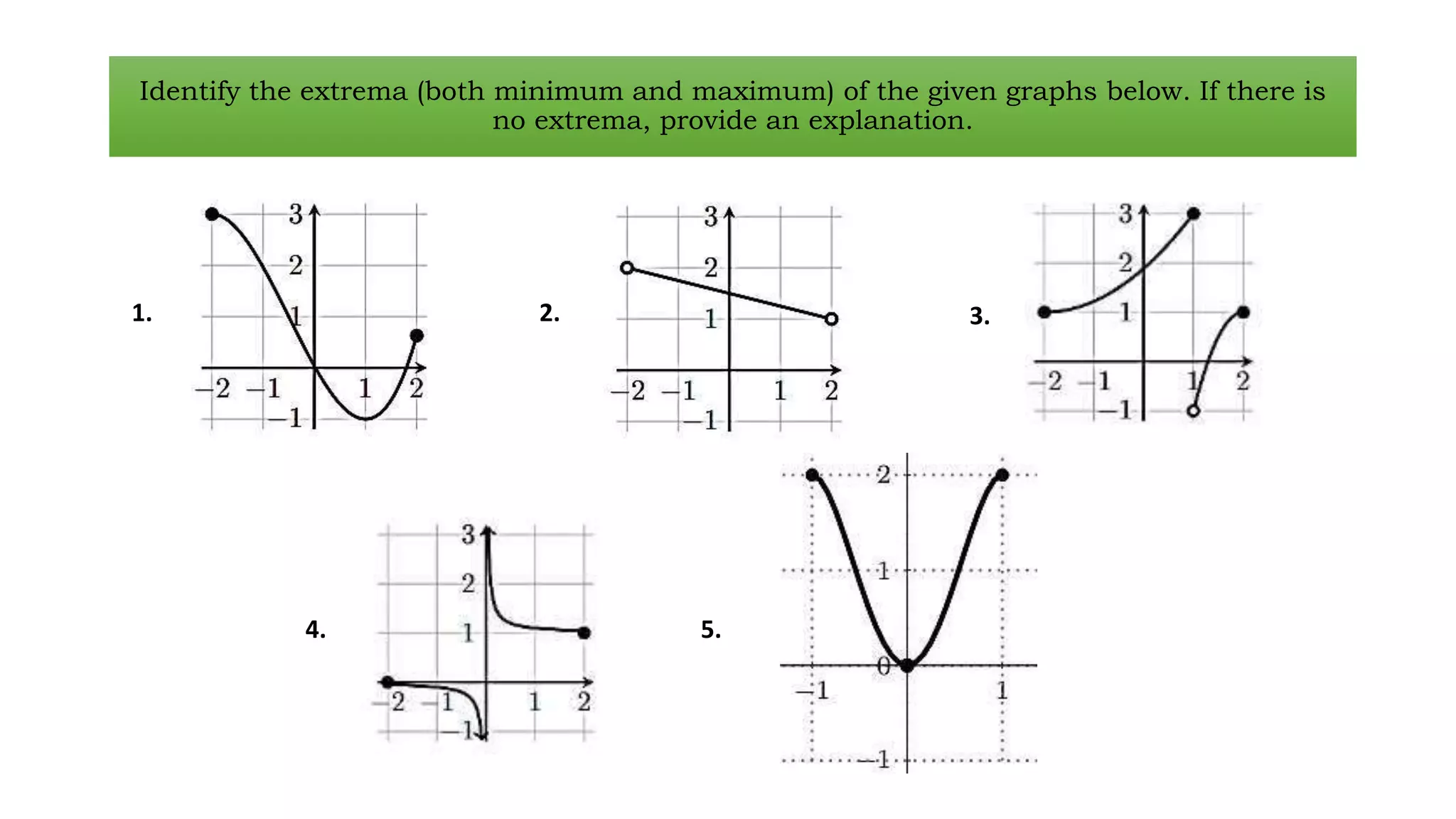
The Extreme Value Theorem states that continuous functions on closed intervals have minimum and maximum values. An extremum is either a minimum or maximum value. A minimum occurs when the function value is less than or equal to all other values in the interval. A maximum occurs when the function value is greater than or equal to all other values in the interval. To find the absolute extrema, take the derivative and set it equal to 0 to find critical points, then substitute these back into the original function to determine the minimum and maximum values.

3. Extreme Value Theorem (EVT)
A function 𝑓(𝑥) which is found to be continuous over a closed interval
[𝑎, 𝑏] is guaranteed to have extreme values in that interval.
An extreme value of 𝑓 or extremum, is either a minimum or maximum
value of a function.
 A minimum value of 𝑓 occurs at
some 𝑥 = 𝑐, if 𝑓(𝑐) ≤ 𝑓(𝑥) for all 𝑥 ≠ 𝑐
in that interval.
A maximum value of 𝑓 occurs at some
𝑥 = 𝑐, if 𝑓(𝑐) ≥ 𝑓(𝑥) for all 𝑥 ≠ 𝑐 in that
interval.

4. Steps in finding the absolute extrema
1. Find the first derivative of he given
function.
2. Equate the first derivative of the given
function to 0.
3. Substitute the given interval and the
critical number (s) to the given function.
4. Select the maximum by finding the largest
value and the minimum by finding the
smallest value in third step.

6. Example 1:
Direction: Find the minimum and maximum value of the function
𝑓 𝑥 = 5𝑥2 + 2𝑥 − 3 at the interval [-3, 2]
1. Find the first derivative of the given
function.
2. Equate the first derivative of the
given function to 0.
3. Substitute the given interval and the
critical number (s) to the given function.
4. Select the maximum by finding the
largest value and the minimum by
finding the smallest value in third
step.

9. Example 2:
Direction: Find the minimum and maximum value of the function
𝑓 𝑥 = 𝑥3 − 7𝑥2 − 5𝑥 + 20 at the interval [-1, 1]
1. Find the first derivative of the given
function.
2. Equate the first derivative of the
given function to 0.
3. Substitute the given interval and the
critical number (s) to the given function.
4. Select the maximum by finding the
largest value and the minimum by
finding the smallest value in third
step.

10. Identify the extrema (both minimum and maximum) of the given graphs below. If there is
no extrema, provide an explanation.
1. 2. 3.
4. 5.

11. Express what you have learned in this lesson by answering
the questions below.
1. When can we say that a function or a
graph has extrema (both minimum
and maximum value)?

12. Express what you have learned in this lesson by answering
the questions below.
2. How do we identify the minimum and
maximum value of the graph of a function at
a given interval?

13. Determine if the given function will have extrema. If it has extrema, identify its
maximum and minimum value. If it has no extrema, provide an explanation. Use a
separate sheet of paper to answer the following.
ACTIVITY!