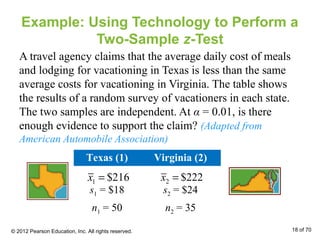
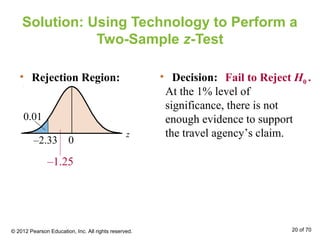
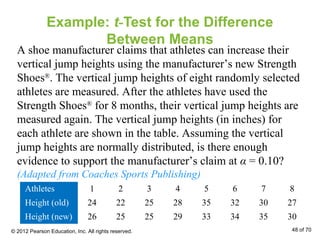
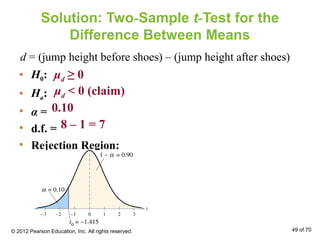
This document outlines how to perform hypothesis tests to compare the means of two independent samples. It discusses using a two-sample z-test when samples are large and normally distributed, and a two-sample t-test when samples are small. The key steps are to state the null and alternative hypotheses, calculate the test statistic, find the critical value, make a decision to reject or fail to reject the null hypothesis, and interpret the results. Examples are provided to demonstrate these tests.