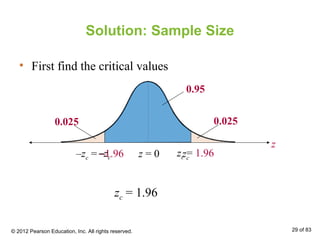
This document outlines key concepts for constructing confidence intervals for a population mean when sample sizes are large or small. It discusses how to find point estimates and margins of error, and how to construct confidence intervals using z-scores or t-statistics depending on sample size. Examples are provided to demonstrate how to calculate critical values, margins of error, and minimum sample sizes needed to estimate population means within a given level of confidence.