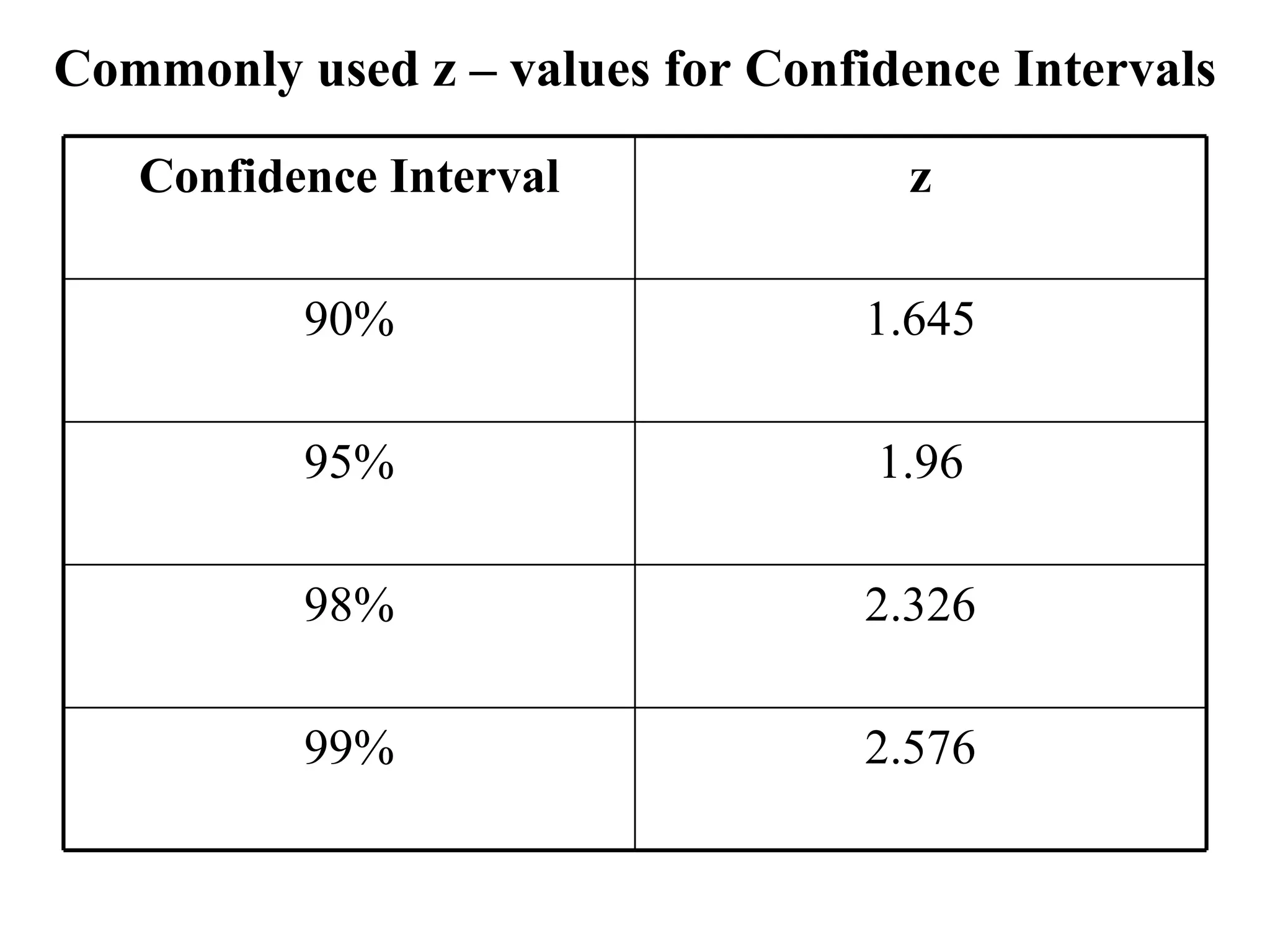
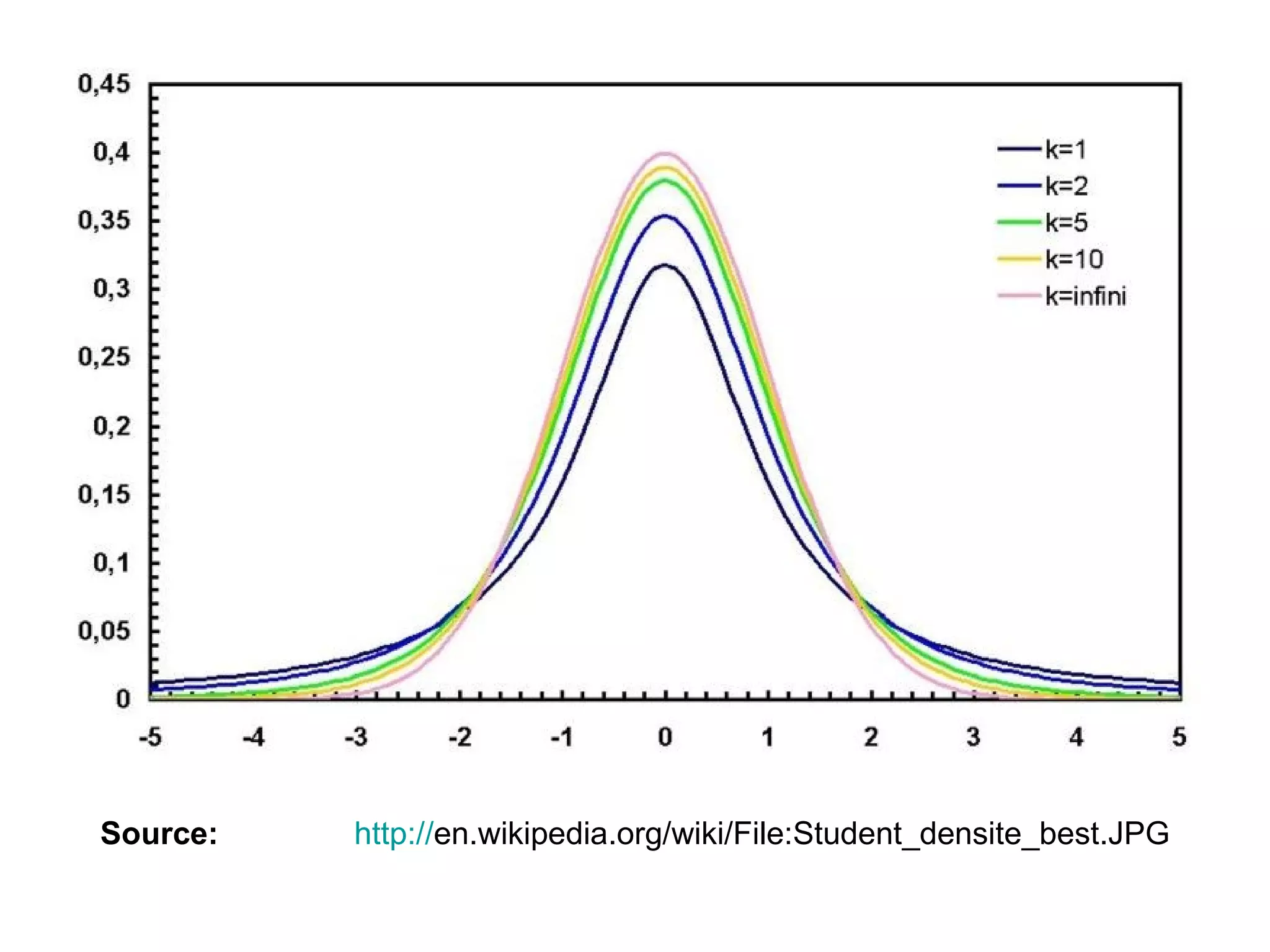
This document provides an overview of key concepts in confidence intervals and the t-distribution covered in Statistics 3, including: 1) Calculating confidence intervals for means from both normal and non-normal populations, whether the population variance is known or unknown. 2) Determining whether to use the z-distribution or t-distribution based on sample size and characteristics. 3) Approximating confidence intervals for population proportions based on large sample sizes from binomial distributions. 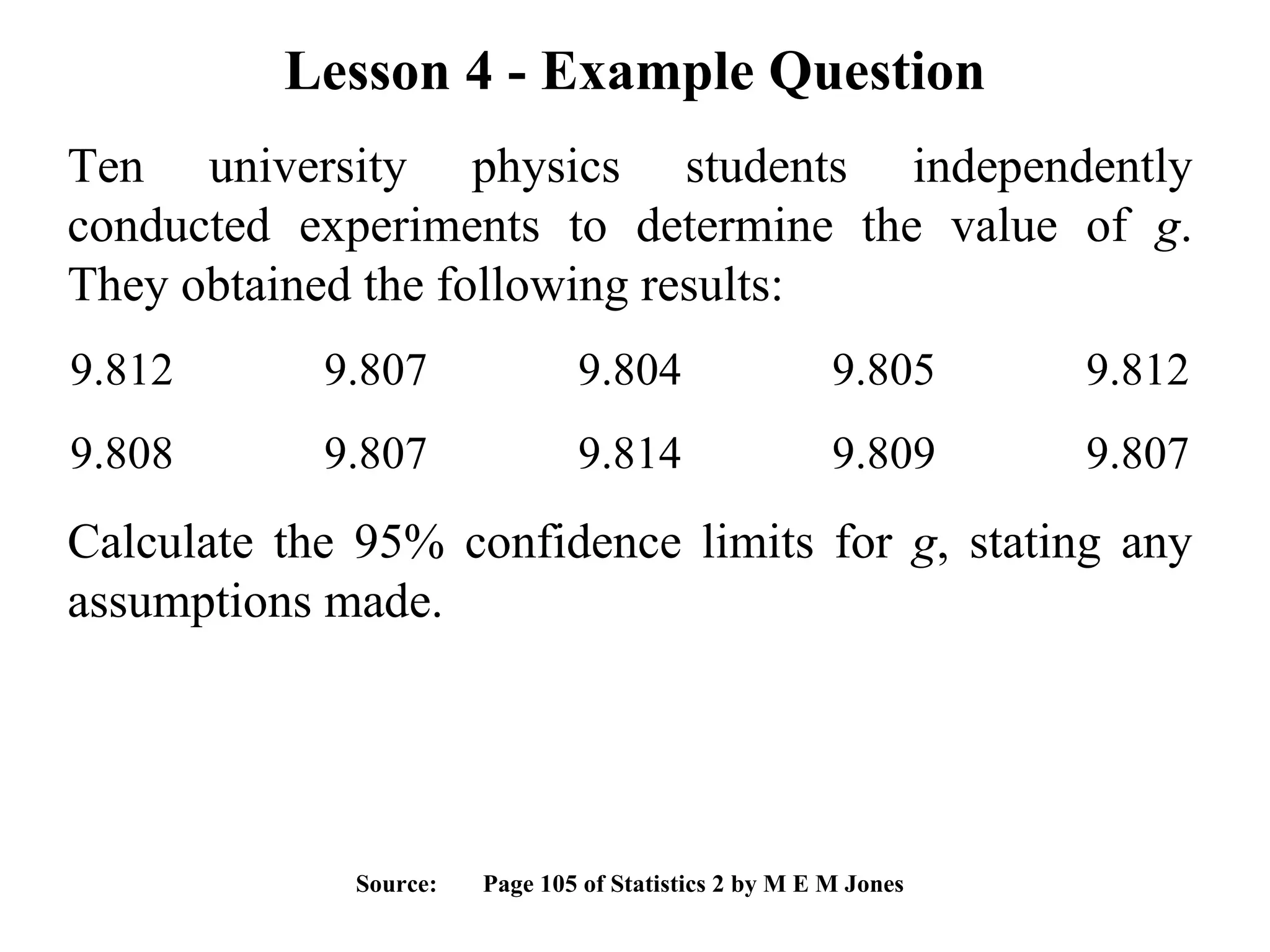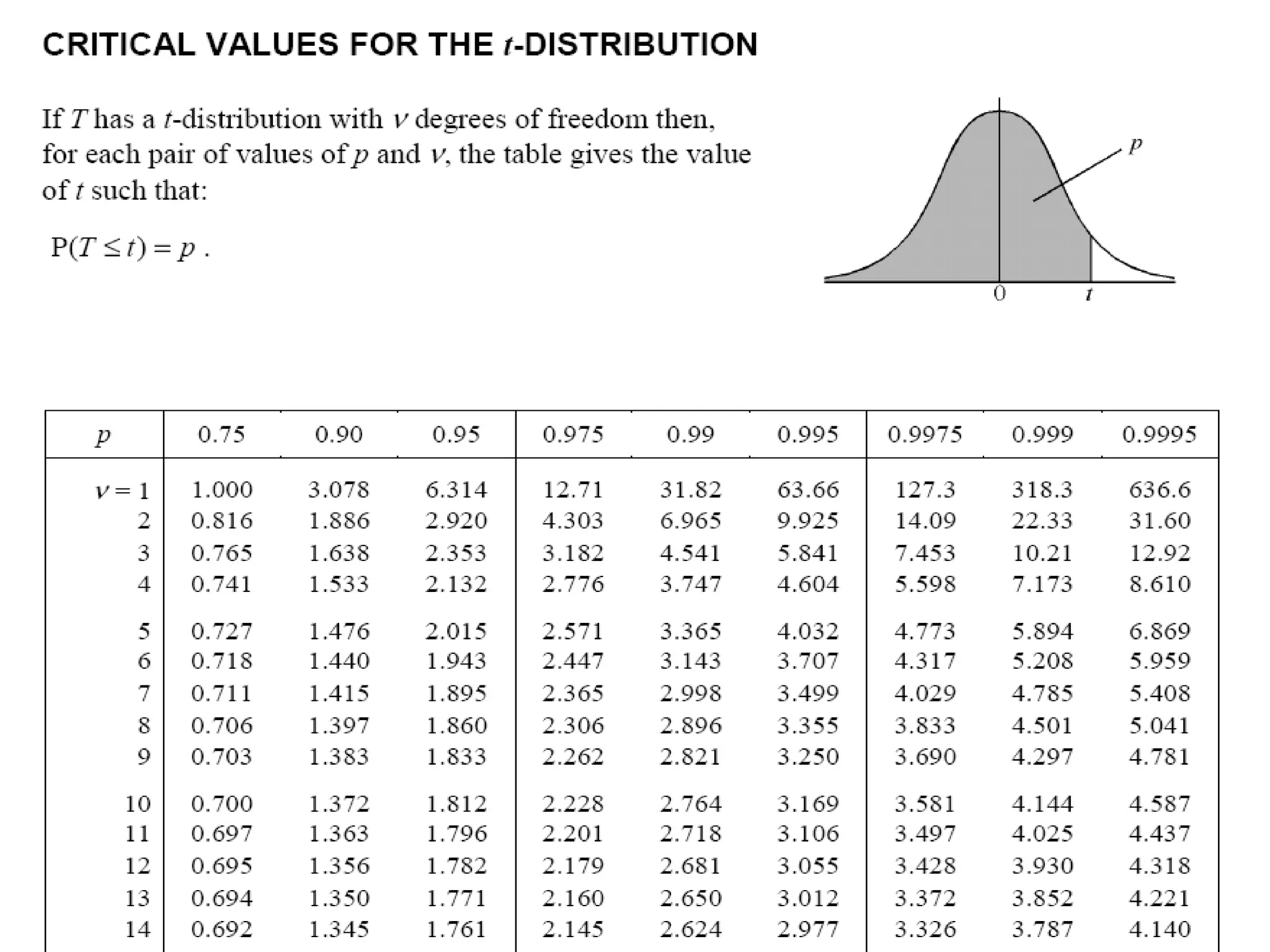4) Using hypothesis tests to evaluate claims about population means based on small samples from normal distributions.

1. Statistics 3 Confidence Intervals and the t - Distribution - Lesson 1 - Key Learning Points/Vocabulary: The concept of a confidence intervals (notes). Calculating a 95% confidence interval for a sample drawn from a normal population of known variance. Calculating any confidence interval.

2. Lesson 1 - Example Question I The heights of the 1320 lower school students at Poole High School are normally distributed with mean μ and with a standard deviation of 10cm. A sample of size 25 is taken and the mean height of the sample is found to be 161cm. a.) Find the 95% confidence interval for the height of the students. b.) If 200 samples of size 25 are taken with a 95% confidence interval being calculated for each sample, find the expected number of intervals that do not contain μ , the population mean.

3. Lesson 1 - Example Question II The masses of sweets produced by a machine are normally distributed with a standard deviation of 0.5 grams. A sample of 50 sweets has a mean mass of 15.21 grams. a.) Find a 99% confidence interval for μ , the mean mass of all sweets produced by the machine correct to 2dp. b.) The manufacturer of the machine claims that is produces sweets with a mean mass of 15 grams, state whether the confidence interval supports this claim. Source: Page 48 of Statistics 3 by Jane Miller

4. Commonly used z – values for Confidence Intervals 2.576 99% 2.326 98% 1.96 95% 1.645 90% z Confidence Interval

5. Generalisation: Sample from a Normal Population A 100(1 – α )% confidence interval of the population mean for a sample of size n taken from a normal population with variance σ 2 is given by where x is the sample mean and the value of z is such that Ф (z) = 1 – ½ α .

6. Practice Questions Statistics 3 and 4 by Jane Miller Page 50, Exercise 3A Question 1 onwards

7. Statistics 3 Confidence Intervals and the t - Distribution - Lesson 2 - Key Learning Points/Vocabulary: The central limit theorem (S2) Unbiased estimate of the population variance (S2). Calculating the confidence interval for a large sample.

8. Unbiased Estimate of the Population Variance Given a sample of size n (n large) from a population of which the variance is unknown, we estimate the population variance s 2 as detailed below:

9. Generalisation: Large Sample for any Population Given a large sample (n>30) from any population, a 100(1 – α )% confidence interval of the population mean is given by where x is the sample mean and the value of z is such that Ф (z) = 1 – ½ α .

10. Lesson 2 - Example Question On 1 st September, 100 new light bulbs were installed in a building, together with a device that detailed for how long each light bulb was used. By 1 st March, all 100 light bulbs had failed. The data for the recorded lifetimes, t (in hours of use), are summarised by Σ t = 10500 and Σ t 2 = 1712500. Assuming that the bulbs constituted a random sample, obtain a symmetric 99% confidence interval for the mean lifetime of the light bulbs, giving your answer correct to the nearest hour. Source: Page 48 of Statistics 3 by Jane Miller

11. Practice Questions Statistics 3 and 4 by Jane Miller Page 50, Exercise 3B Question 1 onwards

12. Statistics 3 Confidence Intervals and the t - Distribution - Lesson 3 - Key Learning Points/Vocabulary: Expectation and variance of the binomial distribution. Conditions for normal approximation to the binomial. Calculating the approximate confidence interval for a population proportion from a large sample.

13. Lesson 3 - Example Question You are the manufacturer of tin openers to be used specifically by left handed people. A random sample of 500 people finds that 60 of them are left handed. What is the 95% confidence interval for this estimate of the proportion of people who are left handed? Source: Page 55 of Statistics 3 by Jane Miller

14. Generalisation: Confidence Interval for a Proportion Given a large random sample of size n from a population in which a proportion of members p has a particular attribute, the approximate confidence interval is given by:

15. Practice Questions Statistics 3 and 4 by Jane Miller Page 50, Exercise 3C Question 3 onwards

16. Statistics 3 Confidence Intervals and the t - Distribution - Lesson 4 - Key Learning Points/Vocabulary: Use flow chart to help decide when to use either the t or z distribution. The t – distribution. Calculating the confidence interval for a small sample drawn from a normal population of unknown variance.

17. Source: http:// en.wikipedia.org/wiki/File:Student_densite_best.JPG

18. Lesson 4 - Example Question Ten university physics students independently conducted experiments to determine the value of g . They obtained the following results: 9.812 9.807 9.804 9.805 9.812 9.808 9.807 9.814 9.809 9.807 Calculate the 95% confidence limits for g , stating any assumptions made. Source: Page 105 of Statistics 2 by M E M Jones

20. Theory For a random sample from a normal population with mean μ , the variable has a t distribution with ν degrees of freedom, where ν = n – 1. That is,

21. Generalisation: t-distribution Given a sample from a normal population of unknown variance, a 100(1 – α )% confidence interval for the population mean is given by where x is the sample mean and the value of t is such that P(T ≤ t) = 1 – ½ α for ν = n – 1 degrees of freedom.

22. Practice Questions Statistics 3 and 4 by Jane Miller Page 62, Exercise 3D Question 2 onwards

23. Statistics 3 Confidence Intervals and the t - Distribution - Lesson 5 - Key Learning Points/Vocabulary: Hypothesis test on the population mean for a small sample from a normal population. Shortened name: t-Test.

24. Lesson 5 - Example Question The weights of eggs laid by a hen when fed on ordinary corn are known to be normally distributed with a mean of 32kg. When a hen was fed on a diet of vitamin enriched corn a random sample of 10 eggs was weighed and the following results (in grams) were recorded: 31, 33, 34, 35, 35, 36, 32, 31, 36, 37 Test, using a 5% significance level, the claim that the new diet has increased the mean weight of eggs laid by the hen by more than 1g. Source: Page 152 or Statistics2 by MEM Junes

25. Practice Questions Statistics 3 and 4 by Jane Miller Page 67, Exercise 3E Question 1 onwards

26. Statistics 3 Confidence Intervals and the t - Distribution - Lesson 6 - Key Learning Points/Vocabulary: Mixed questions on Confidence Intervals and the t-Distribution. Mind map to summarise key learning points.

27. Practice Questions Statistics 3 and 4 by Jane Miller Page 687, Miscellaneous Exercise 3 Questions 1, 3, 6 and 9 (first part only)