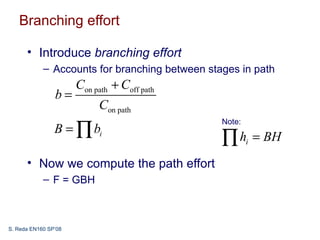
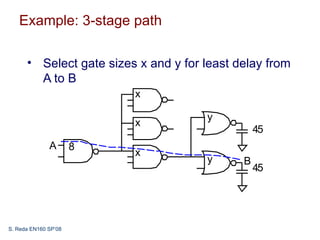
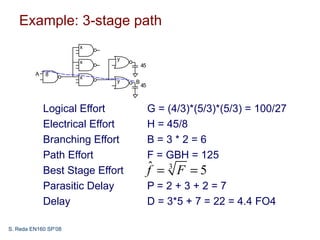
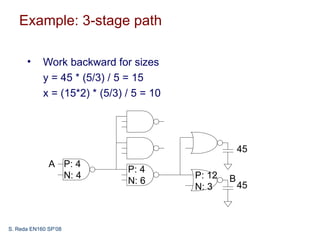
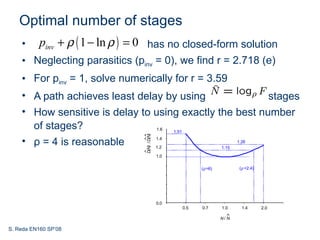
This document discusses logical effort and how it can be used to analyze multistage logic networks. It explains that logical effort can be generalized to account for branching in multistage paths. When branching is considered, the path effort is equal to the product of logical effort, electrical effort, and branching effort. Logical effort analysis can also be used to determine the optimal size of each stage and number of stages to minimize delay in a multistage network.

1. Design and Implementation of VLSI Systems
(EN1600)
Lecture 13: Logical Effort (2/2)
S. Reda EN160 SP’08

2. Multistage logic networks
• Logical effort generalizes to multistage networks
• Path Logical Effort G = ∏ gi
Cout-path
• Path Electrical Effort H=
Cin-path
• Path Effort F = ∏ f i = ∏ gi hi
10
x z
y
20
g1 = 1 g2 = 5/3 g3 = 4/3 g4 = 1
h1 = x/10 h2 = y/x h3 = z/y h4 = 20/z
Can we write F=GH?
S. Reda EN160 SP’08

3. Can we write F = GH?
• No! Consider paths that branch:
G =1 15
90
H = 90 / 5 = 18
5
GH = 18
h1 = (15 +15) / 5 = 6 15
90
h2 = 90 / 15 = 6
F = g1g2h1h2 = 36 = 2GH
How to fix this problem?
S. Reda EN160 SP’08

4. Branching effort
• Introduce branching effort
– Accounts for branching between stages in path
Con path + Coff path
b=
Con path
B = ∏ bi
Note:
∏h i = BH
• Now we compute the path effort
– F = GBH
S. Reda EN160 SP’08

5. Logical Effort can help us answering two key
questions
1. How large should be each stage in a multi-
stage network to achieve the minimium delay?
2. What is the optimal number of stages to
achieve the minimum delay
S. Reda EN160 SP’08

6. 1. What is the optimal size of each stage?
Gate Gate
1 2
GND
Delay is minimized when each stage bears the same effort
Answer can be generalized. Thus, for N stages, minimum delay
is achieved when each stage bears the same effort
S. Reda EN160 SP’08

7. Example: 3-stage path
• Select gate sizes x and y for least delay from
A to B
x
y
x
45
A 8
x
y B
45
S. Reda EN160 SP’08

8. Example: 3-stage path
x
y
x
45
A 8
x
y B
45
Logical Effort G=
Electrical Effort H=
Branching Effort B=
Path Effort F=
Best Stage Effort ˆ
f =
Parasitic Delay P=
Delay D=
S. Reda EN160 SP’08

9. Example: 3-stage path
x
y
x
45
A 8
x
y B
45
Logical Effort G = (4/3)*(5/3)*(5/3) = 100/27
Electrical Effort H = 45/8
Branching Effort B=3*2=6
Path Effort F = GBH = 125
Best Stage Effort ˆ
f = 3 F =5
Parasitic Delay P=2+3+2=7
Delay D = 3*5 + 7 = 22 = 4.4 FO4
S. Reda EN160 SP’08

10. Example: 3-stage path
• Work backward for sizes
y = 45 * (5/3) / 5 = 15
x = (15*2) * (5/3) / 5 = 10
45
A P: 4
P: 4
N: 4 P: 12 B
N: 6 45
N: 3
S. Reda EN160 SP’08

11. 2. What is the optimal number of stages?
• Consider adding inverters to end of path
– How many give least delay? Logic Block:
N - n1 ExtraInverters
n1Stages
n1 Path Effort F
D = NF + ∑ pi + ( N − n1 ) pinv
1
N
i =1
∂D 1 1 1
= − F ln F + F + pinv = 0
N N N
∂N
1
Define best stage effort ρ = F N
pinv + ρ ( 1 − ln ρ ) = 0
S. Reda EN160 SP’08

12. Optimal number of stages
• pinv + ρ ( 1 − ln ρ ) = 0 has no closed-form solution
• Neglecting parasitics (pinv = 0), we find r = 2.718 (e)
• For pinv = 1, solve numerically for r = 3.59
• A path achieves least delay by using stages
• How sensitive is delay to using exactly the best number
of stages? 1.6
1.51
D(N) /D(N)
• ρ = 4 is reasonable 1.4
1.2 1.15
1.26
1.0
(ρ=6) (ρ =2.4)
0.0
0.5 0.7 1.0 1.4 2.0
N/ N
S. Reda EN160 SP’08