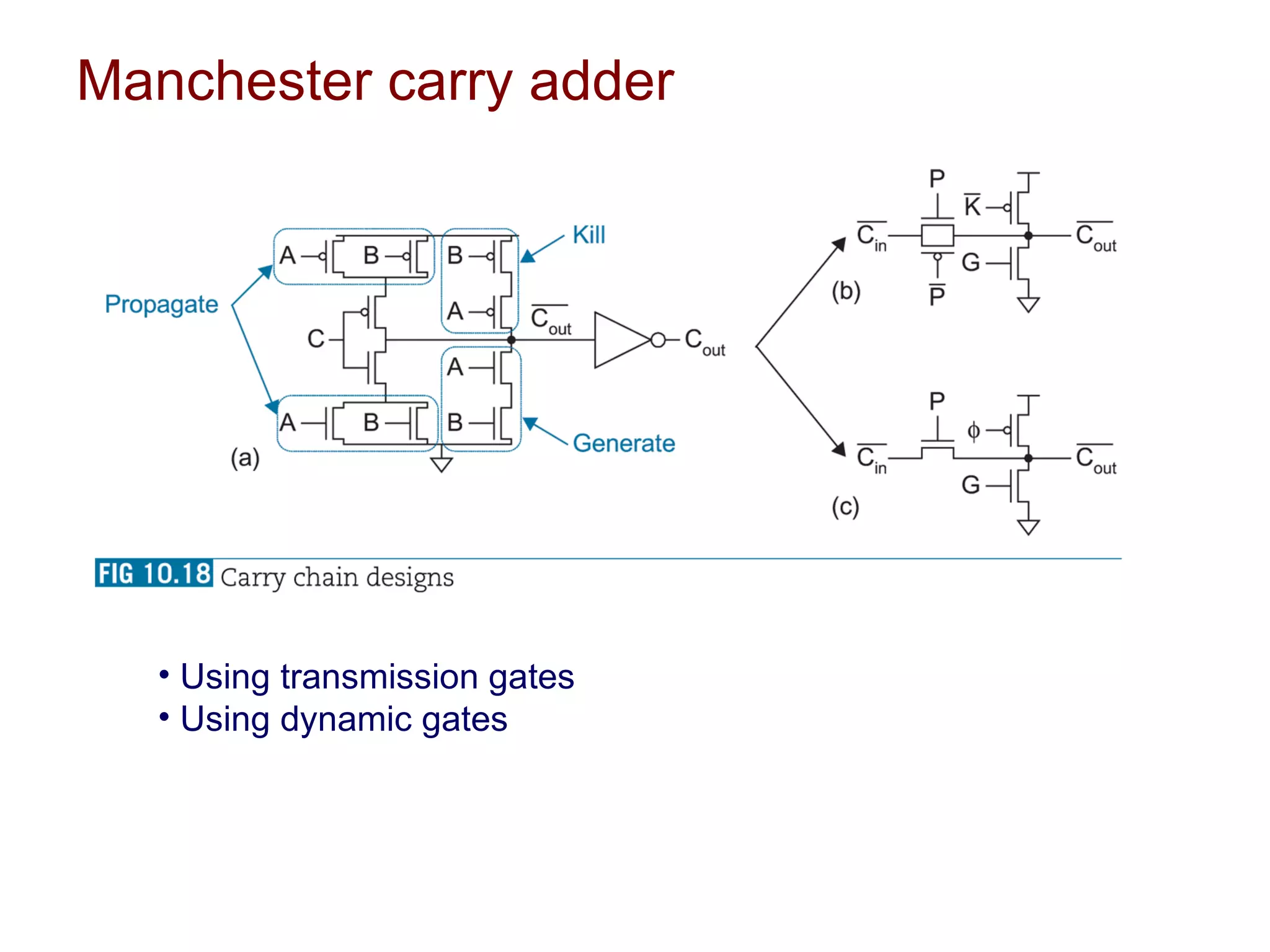
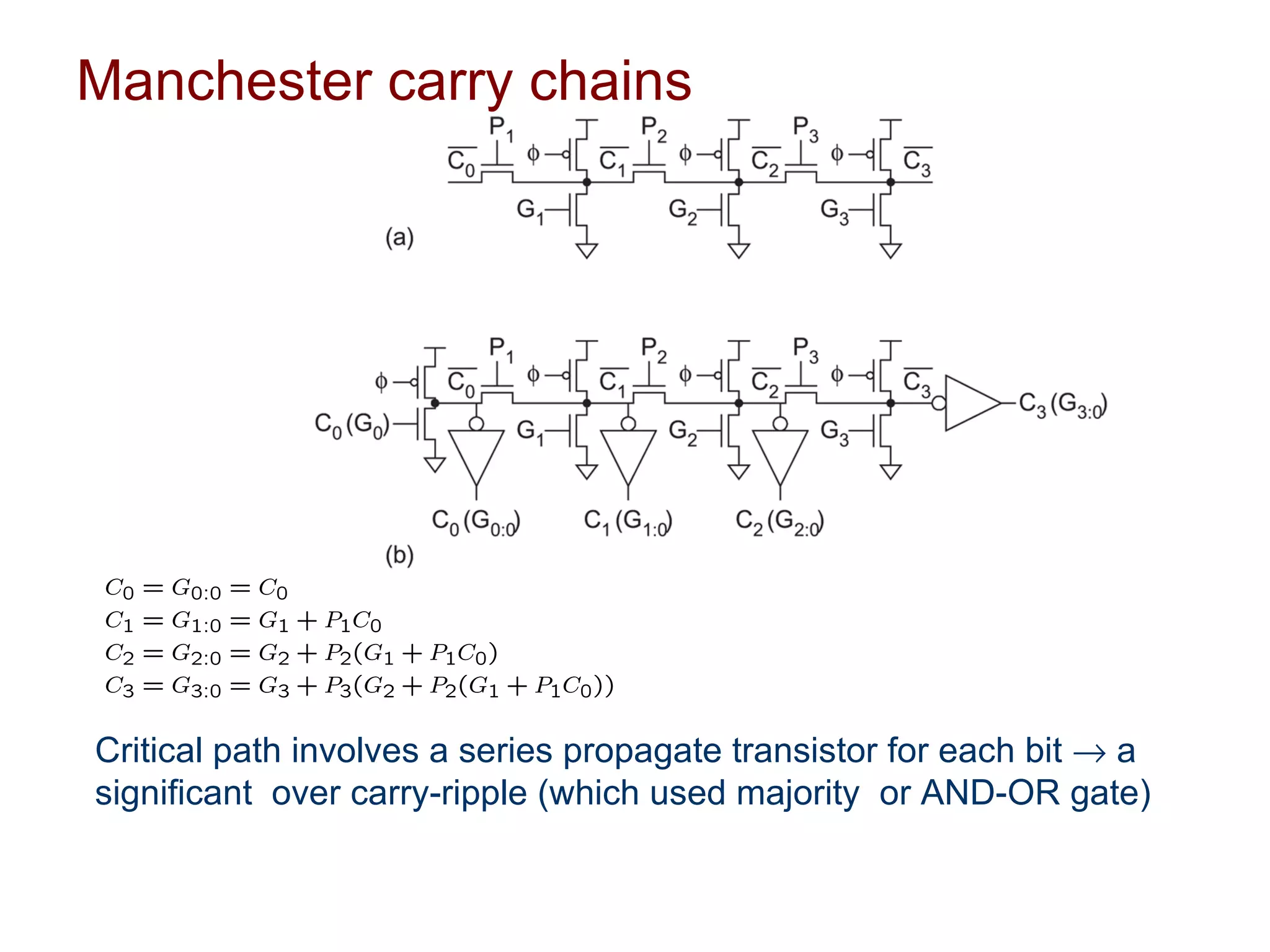
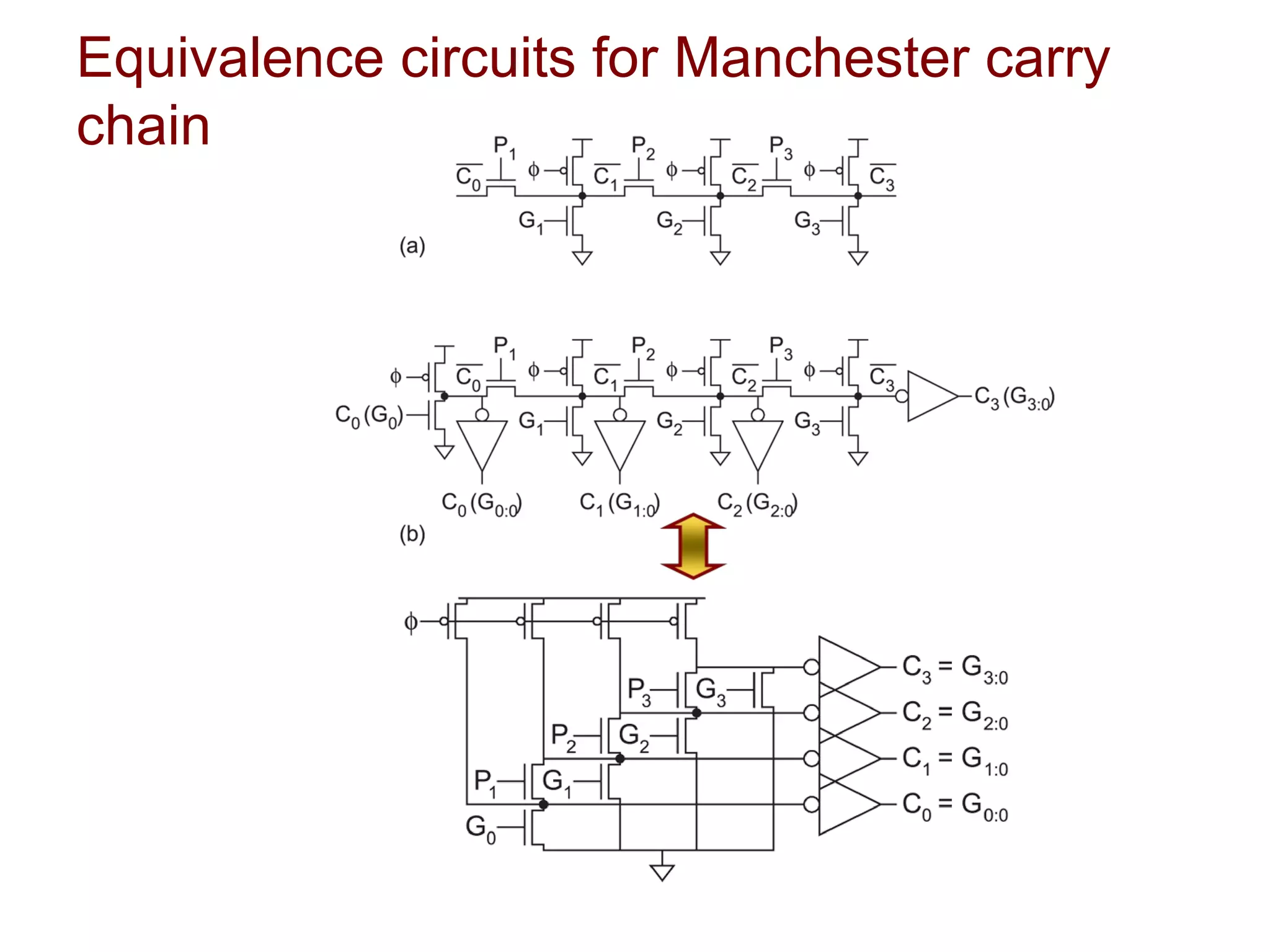
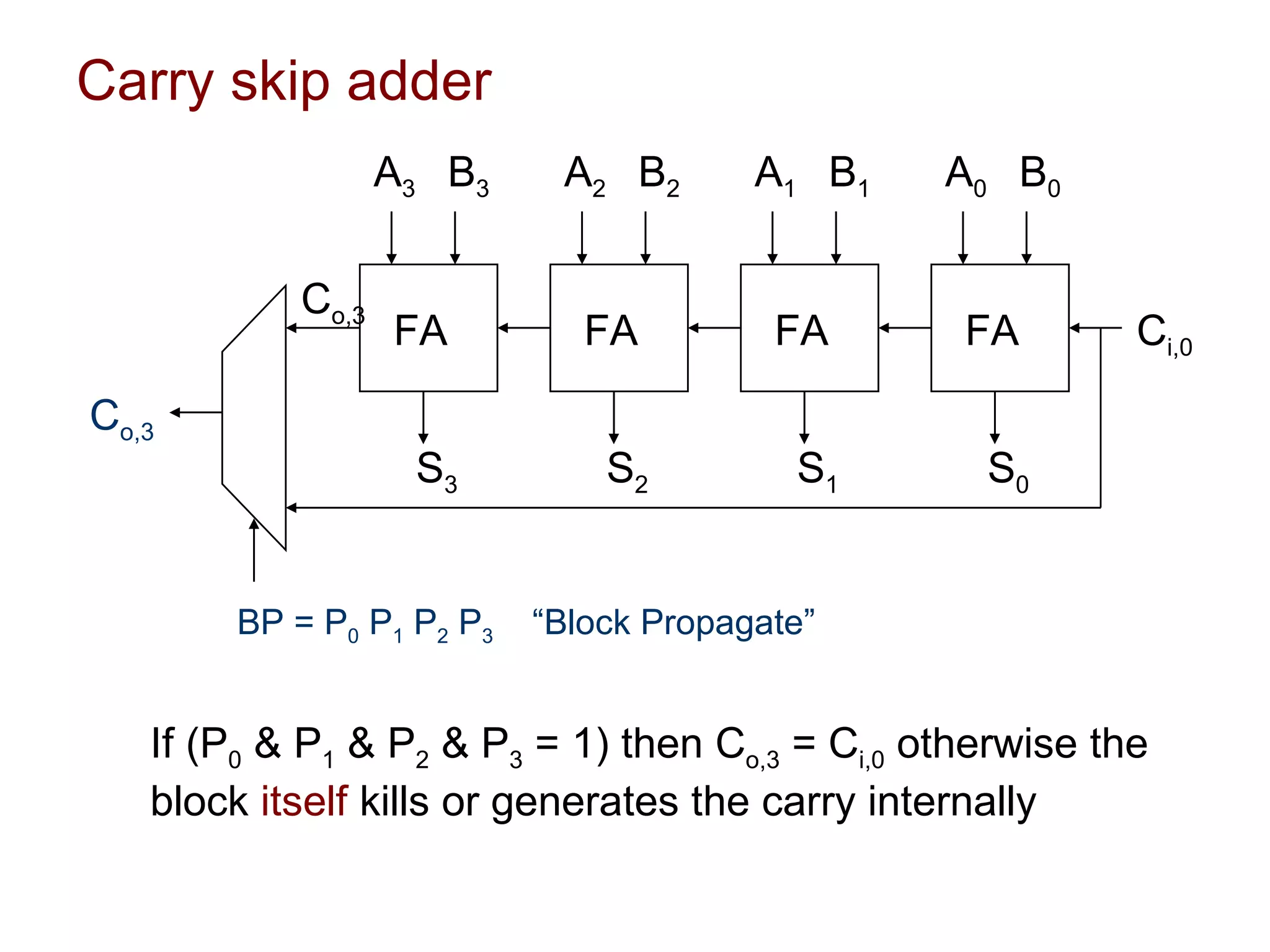
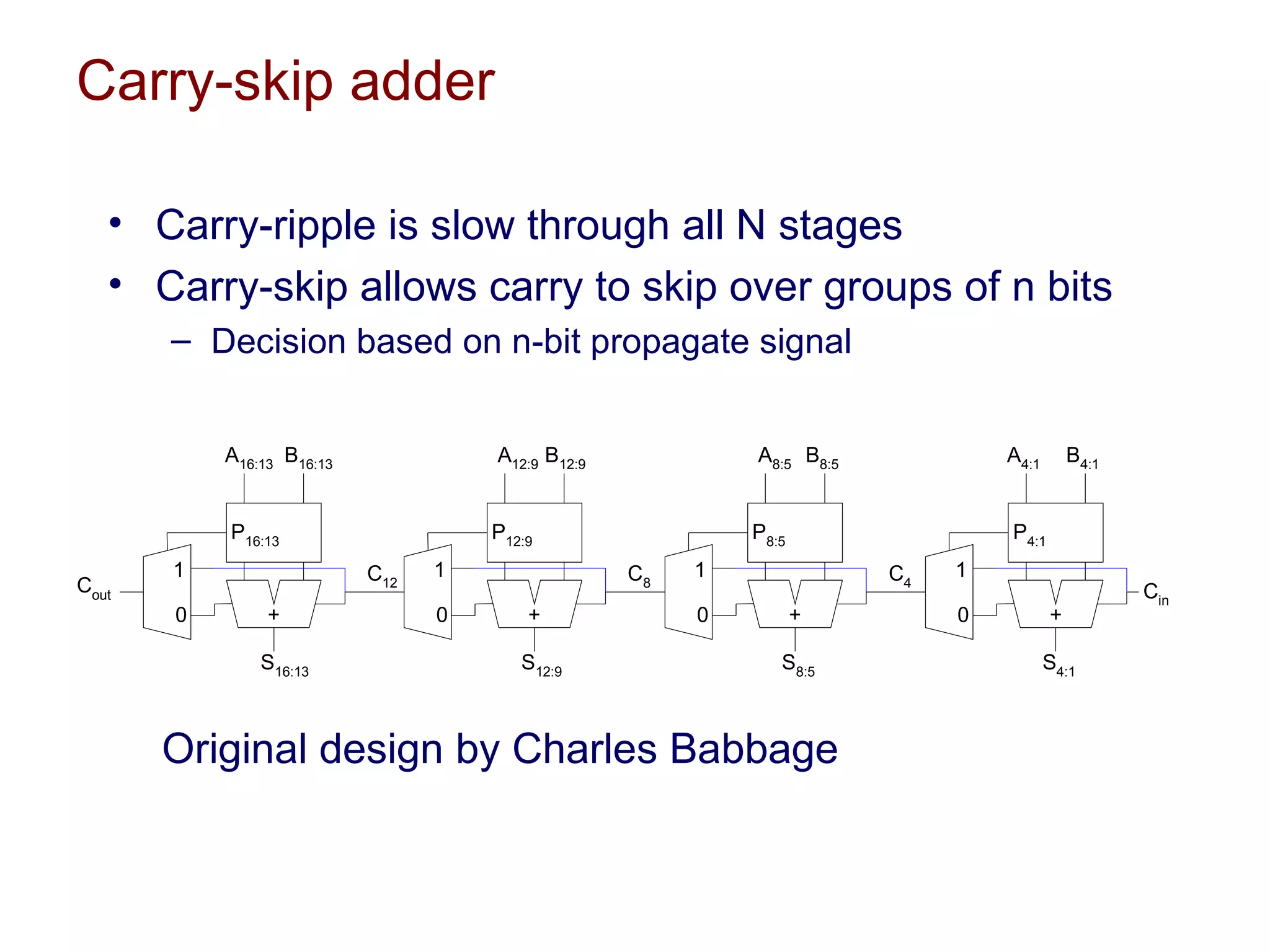
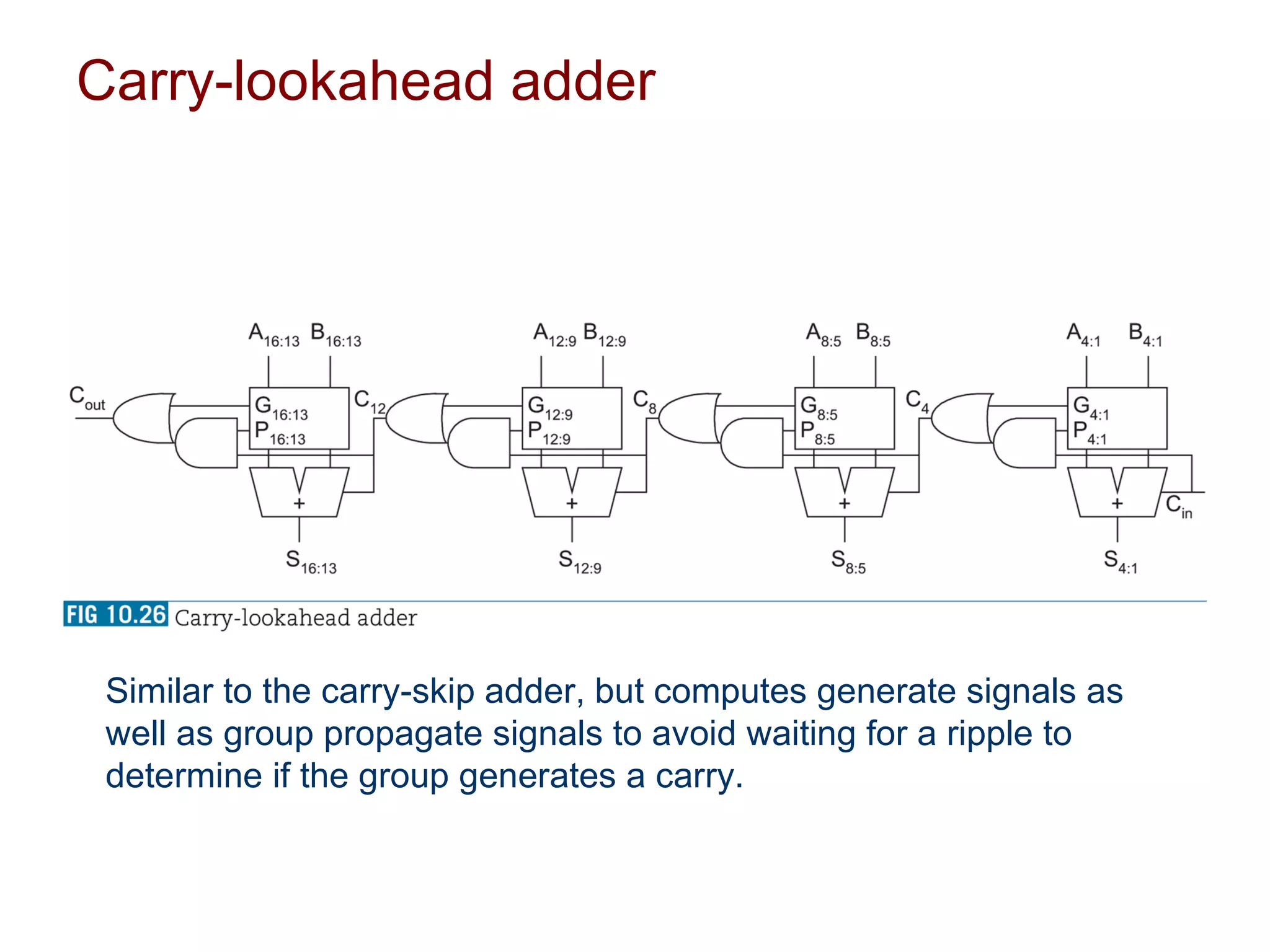
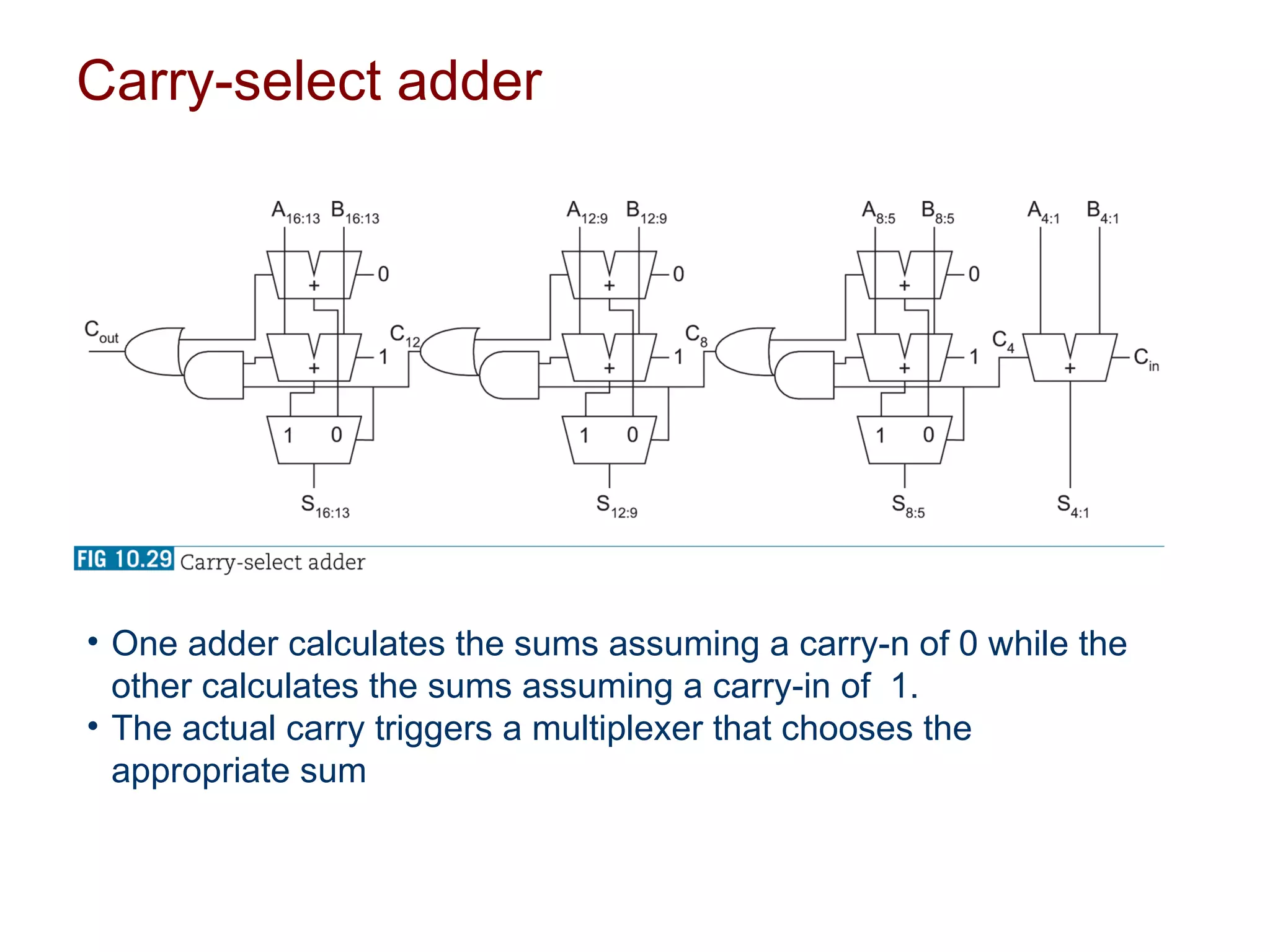
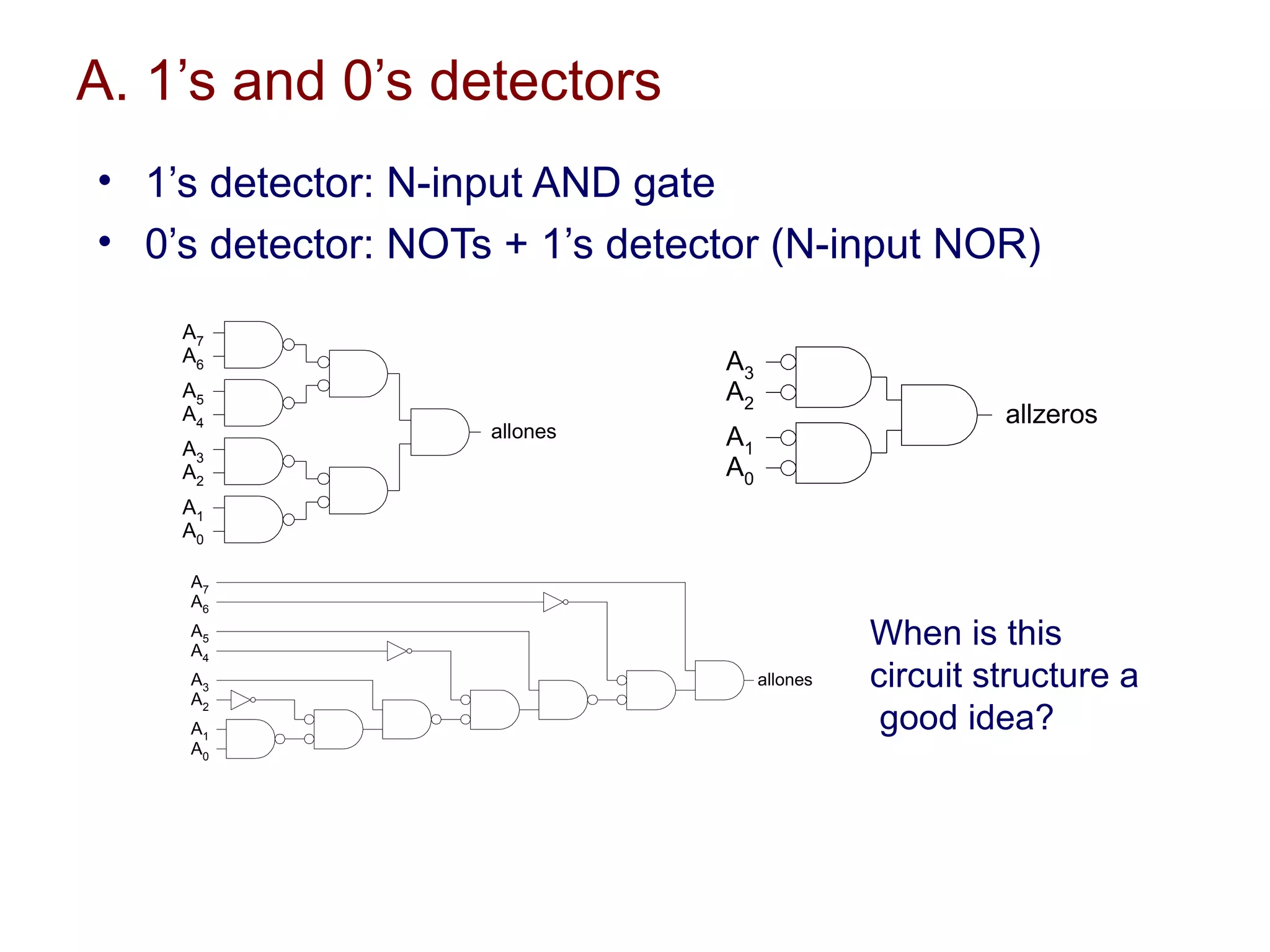
The document summarizes different types of datapath subsystems used in VLSI systems including Manchester carry adders, carry-skip adders, carry-lookahead adders, and carry-select adders. It also discusses different comparator circuits including 0's and 1's detectors, an equality comparator to check if each bit is equal, and a magnitude comparator that computes B-A and looks at the sign bit to determine if A is less than, greater than, or equal to B.

1. Design and Implementation of VLSI Systems
(EN1600)
Lecture 27: Datapath Subsystems 3/4

2. Manchester carry adder
• Using transmission gates
• Using dynamic gates

3. Manchester carry chains
Critical path involves a series propagate transistor for each bit → a
significant over carry-ripple (which used majority or AND-OR gate)

4. Equivalence circuits for Manchester carry
chain

5. Carry skip adder
A3 B3 A2 B2 A1 B1 A0 B0
Co,3
FA FA FA FA Ci,0
Co,3
S3 S2 S1 S0
BP = P0 P1 P2 P3 “Block Propagate”
If (P0 & P1 & P2 & P3 = 1) then Co,3 = Ci,0 otherwise the
block itself kills or generates the carry internally

6. Carry-skip adder
• Carry-ripple is slow through all N stages
• Carry-skip allows carry to skip over groups of n bits
– Decision based on n-bit propagate signal
A16:13 B16:13 A12:9 B12:9 A8:5 B8:5 A4:1 B4:1
P16:13 P12:9 P8:5 P4:1
1 C12 1 C8 1 C4 1
Cout Cin
0 + 0 + 0 + 0 +
S16:13 S12:9 S8:5 S4:1
Original design by Charles Babbage

7. Carry-lookahead adder
Similar to the carry-skip adder, but computes generate signals as
well as group propagate signals to avoid waiting for a ripple to
determine if the group generates a carry.

8. Carry-select adder
• One adder calculates the sums assuming a carry-n of 0 while the
other calculates the sums assuming a carry-in of 1.
• The actual carry triggers a multiplexer that chooses the
appropriate sum

9. II. Comparators
A. 0’s detector and 1’s detectors
B. Equality comparator: A = B
C. Magnitude comparator: A < B

10. A. 1’s and 0’s detectors
• 1’s detector: N-input AND gate
• 0’s detector: NOTs + 1’s detector (N-input NOR)
A7
A6 A3
A5 A2
A4 allzeros
allones A1
A3
A2 A0
A1
A0
A7
A6
A5
A4
When is this
A3 allones circuit structure a
A2
A1 good idea?
A0

11. B. Equality comparator
• Check if each bit is equal (XNOR, aka equality gate)
• 1’s detect on bitwise equality
B[3]
A[3]
B[2]
A[2] A=B
B[1]
A[1]
B[0]
A[0]

12. C. Magnitude comparator
Compute B-A and look at sign
B-A = B + ~A + 1
For unsigned numbers, carry out is sign bit
A≤ B
C
B3
N A≥ B
A3
B2
A2 Z
A=B
B1
A1
B0
A0