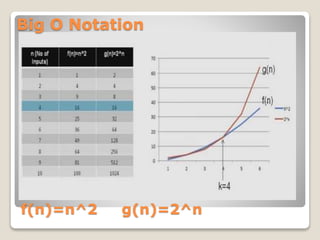
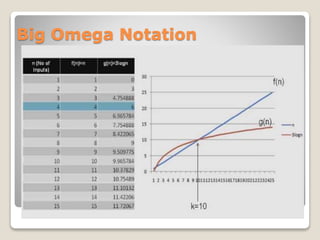
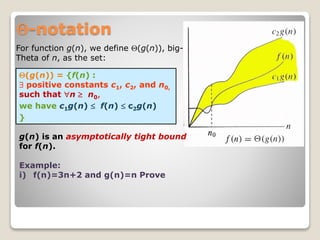
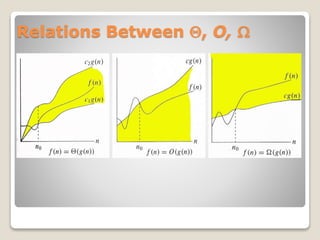
This document introduces asymptotic notations that are used to describe the time complexity of algorithms. It defines big O, big Omega, and big Theta notations, which describe the limiting behavior of functions. Big O notation provides an asymptotic upper bound, big Omega provides a lower bound, and big Theta provides a tight bound. Examples are given of different asymptotic efficiency classes like constant, logarithmic, linear, quadratic, and exponential time. Properties of asymptotic notations like transitivity, reflexivity, symmetry, and transpose symmetry are also covered.

1. Asymptotic Notations

2. Introduction
 In mathematics, computer science, and related fields, big O
notation describes the limiting behavior of a function when the
argument tends towards a particular value or infinity, usually in
terms of simpler functions.
 The time complexity of an algorithm quantifies the amount of
time taken by an algorithm to run as a function of the size of the
input to the problem. When it is expressed using big O notation,
the time complexity is said to be described asymptotically, i.e.,
as the input size goes to infinity.

3. Asymptotic Complexity
 Running time of an algorithm as a function of input size n for large
n.
 Expressed using only the highest-order term in the expression for
the exact running time.
◦ Instead of exact running time, say Q(n2).
 Describes behavior of function in the limit.
 Written using Asymptotic Notation.
 The notations describe different rate-of-growth relations between
the defining function and the defined set of functions.

4. Big O-notation
O(g(n)) = {f(n) :
 positive constants c and n0, such
that n  n0,
we have f(n)  cg(n) }
For function g(n), we define O(g(n)),
big-O of n, as the set:
g(n) is an asymptotic upper bound
for f(n).
Example:
i) f(n)=3n+2 and g(n)=n Prove f(n)  cg(n)
ii) f(n)=100n+5 and g(n)=n2 Prove f(n)  cg(n)

5. f(n)=n^2 g(n)=2^n
Big O Notation

6.  -notation
g(n) is an asymptotic lower bound
for f(n).
Example:
i) f(n)=3n+2 and g(n)=n Prove f(n) >= cg(n)
ii) f(n)=n3 and g(n)=n2 Prove f(n) >= cg(n)
(g(n)) = {f(n) :
 positive constants c and n0, such
that n  n0,
we have cg(n)  f(n) or
f(n)>=cg(n)}
For function g(n), we define (g(n)), big-
Omega of n, as the set:

7. Big Omega Notation

8. Q-notation
Q(g(n)) = {f(n) :
 positive constants c1, c2, and n0,
such that n  n0,
we have c1g(n)  f(n)  c2g(n)
}
For function g(n), we define Q(g(n)), big-
Theta of n, as the set:
g(n) is an asymptotically tight bound
for f(n).
Example:
i) f(n)=3n+2 and g(n)=n Prove

9. Relations Between Q, O, 

10. Basic Asymptotic Efficiency classes
C constant, we write
O(1)
logN logarithmic
log2N log-squared
N linear
NlogN
N2 quadratic
N3 cubic
2N exponential
N! factorial

11. Properties of Asymptotic Notation
1. Transitive
If f(n) = Θ(g(n)) and g(n) = Θ(h(n)), then f(n) = Θ(h(n))
If f(n) = O(g(n)) and g(n) = O(h(n)), then f(n) = O(h(n))
If f(n) = Ω(g(n)) and g(n) = Ω(h(n)), then f(n) = Ω(h(n))
2. Reflexivity
f(n) = Θ(f(n))
f(n) = O(f(n))
f(n) = Ω(f(n))
3. Symmetry
f(n) = Θ(g(n)) if and only if g(n) = Θ(f(n))
4. Transpose Symmetry
f(n) = O(g(n)) if and only if g(n) = Ω(f(n))

12. The End