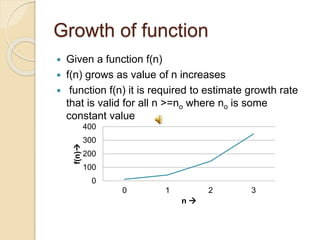
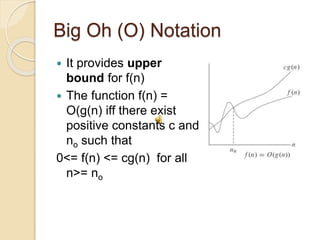
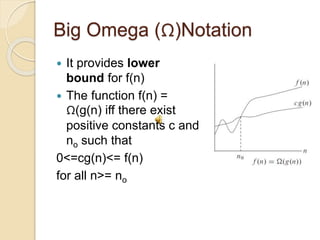
The document discusses asymptotic notations used to estimate the growth rate of functions. It defines asymptotic notations like Big-O, Big-Omega, and Theta that provide upper, lower, and tight bounds. Examples show how to determine if a function f(n) is O(g(n)), Ω(g(n)), or Θ(g(n)) based on constants. Little-o and little-omega notations describe bounds that are not asymptotically tight. Asymptotic notations are useful for analyzing time complexities of algorithms.

1. Growth of function
&
Asymptotic Notations
By
Mamata Pandey

2. Growth of function
 Given a function f(n)
 f(n) grows as value of n increases
 function f(n) it is required to estimate growth rate
that is valid for all n >=no where no is some
constant value
0
100
200
300
400
0 1 2 3
f(n)
n 

3. Asymptote
 Asymptote is a line or curve
represented by a function say g(n) that
approaches a given curve say f(n) but
never reaches as they tend to infinity
 We can say f(n) grows like g(n) i.e.
growth of function is considered like
g(n)
 It is said that f(n) is asymptotically
bound by g(n)

4. What are Asymptotic
Notations
 For a given function f(n) asymptotic
notations Asymptotic notations are
used estimate or to bound the growth
of f(n) in terms of other simpler
function g(n) like n, n2, log(n) etc.
 They provide approximate but
meaningful assumptions about
complexity of f(n)

5. Asymptotic Notations
 Big Oh notation
 Big Omega notation
 Big Theta notation
 Little oh notation
 Little omega notation

6. Big Oh (O) Notation
 It provides upper
bound for f(n)
 The function f(n) =
O(g(n) iff there exist
positive constants c and
no such that
0<= f(n) <= cg(n) for all
n>= no

7. Big Omega (Ω)Notation
 It provides lower
bound for f(n)
 The function f(n) =
Ω(g(n) iff there exist
positive constants c and
no such that
0<=cg(n)<= f(n)
for all n>= no

8. Theta( )Notation
 It provides tight bound
for f(n)
 The function f(n) =
(g(n) iff there exist
positive constants c1
and c2, and no such that
c1g(n)<= f(n) <= c2g(n)
for all n>= no
~
~

9. Little oh (o) Notation
 Little o-notation to denote an upper
bound that is not asymptotically tight.
 The function f(n) = o(g(n)) iff there
exist positive constants c and no such
that
0<= f(n) < cg(n) for all n>= no
 in o-notation, the function f (n)
becomes insignificant relative to g(n)
as n approaches infinity; that is,

10. Little omega (w ) Notation
 w –notation is used to denote a lower
bound that is not asymptotically tight
 The function f(n) = w(g(n)) iff there
exist positive constants c and no such
that0<=cg(n)< f(n) for all n>= no
 The relation implies that f(n) becomes
arbitrarily large relative to g(n)as n
approaches infinity. That is,

11. Example:
 f(n)= 7n3-3n2 +5n+12
 or, f(n) ≤ |7n3|+|-3n2 |+|5n|+|12|
 or, f(n) ≤ 7n3+3n3 +5n3+12n3
 or, f(n) ≤ 27n3
 or, f(n)=O(n3) where c=27 and no=0

12. Example
 f(n)= 7n3-3n2 +5n+12
 or, f(n) ≥ 7n3
 or, f(n) =Ω (n3) where c=7 and no=0
Now,
 7n3 ≤ f(n) ≤ 27n3
 or, f(n) = (n3) where c1=7 ,c2=27 and
no=0
~

13. Example:
 Let f(n)= (n3),
Here n3 provides tight bound hence
f(n)=O(n3) and f(n)= Ω(n3), then
 f(n) ≥ c n3 ≥ c n2 ≥ cn ≥ c and
 f(n) ≤ c’ n3 ≤ c’n4 ≤ c’n5… ≤ c’nm
where c, c’ c1, c2 , c3 are constants
and m>=3
~

14.  But n2, n and c provide lower bound
which is not tight hence
 f(n) = w(n2)= w(n)= w(c)
 Simillarly n4, n5 or any higher power of
n provides lower bound that is not
asymptotically tight.
 f(n) = o(n4)= o(n5)= ……=o(nm)

15. Application of asymptotic
notations
 Calculating and comparing time
complexities of algorithms
 f(n) is a function representing number
of operations for a problem of size n