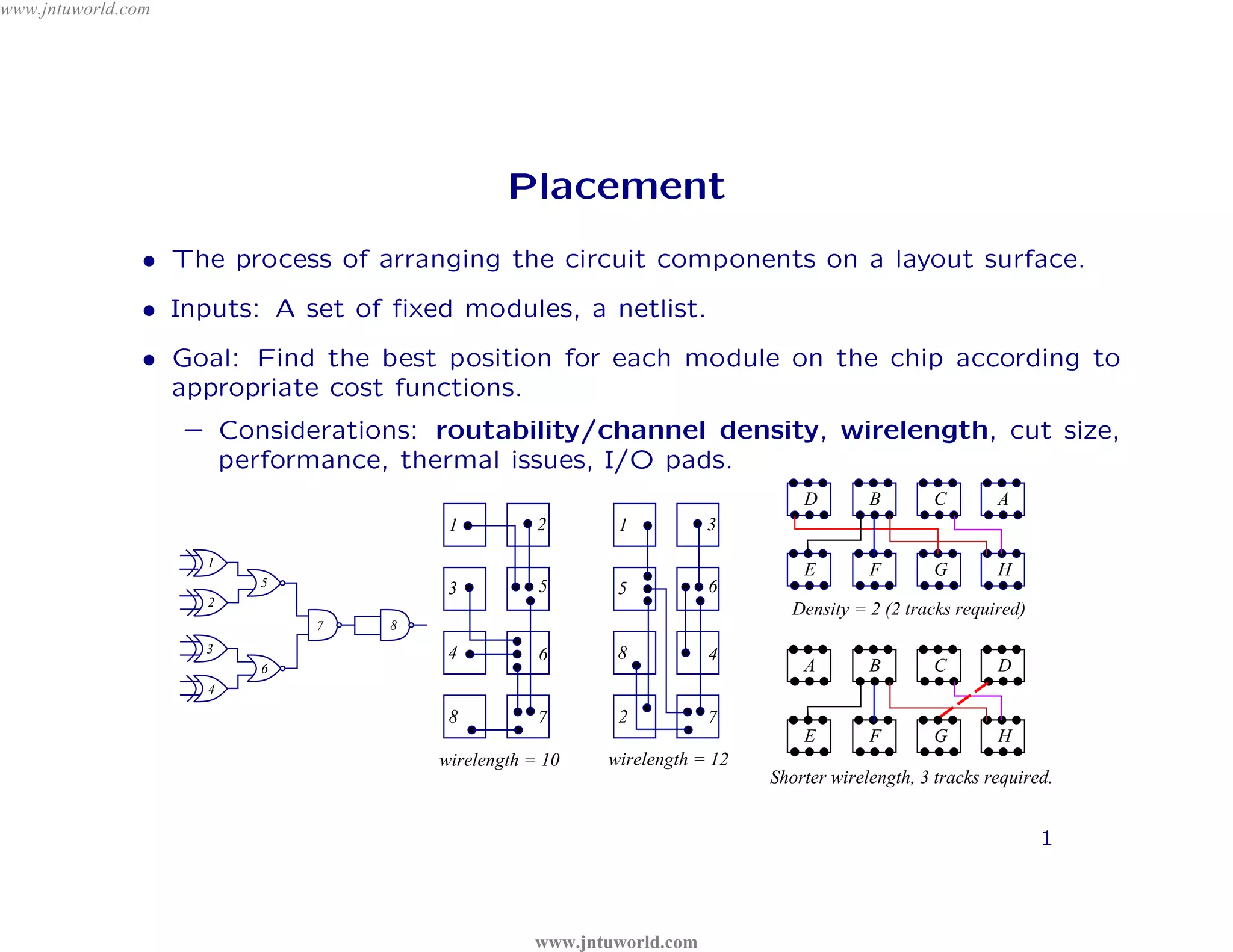
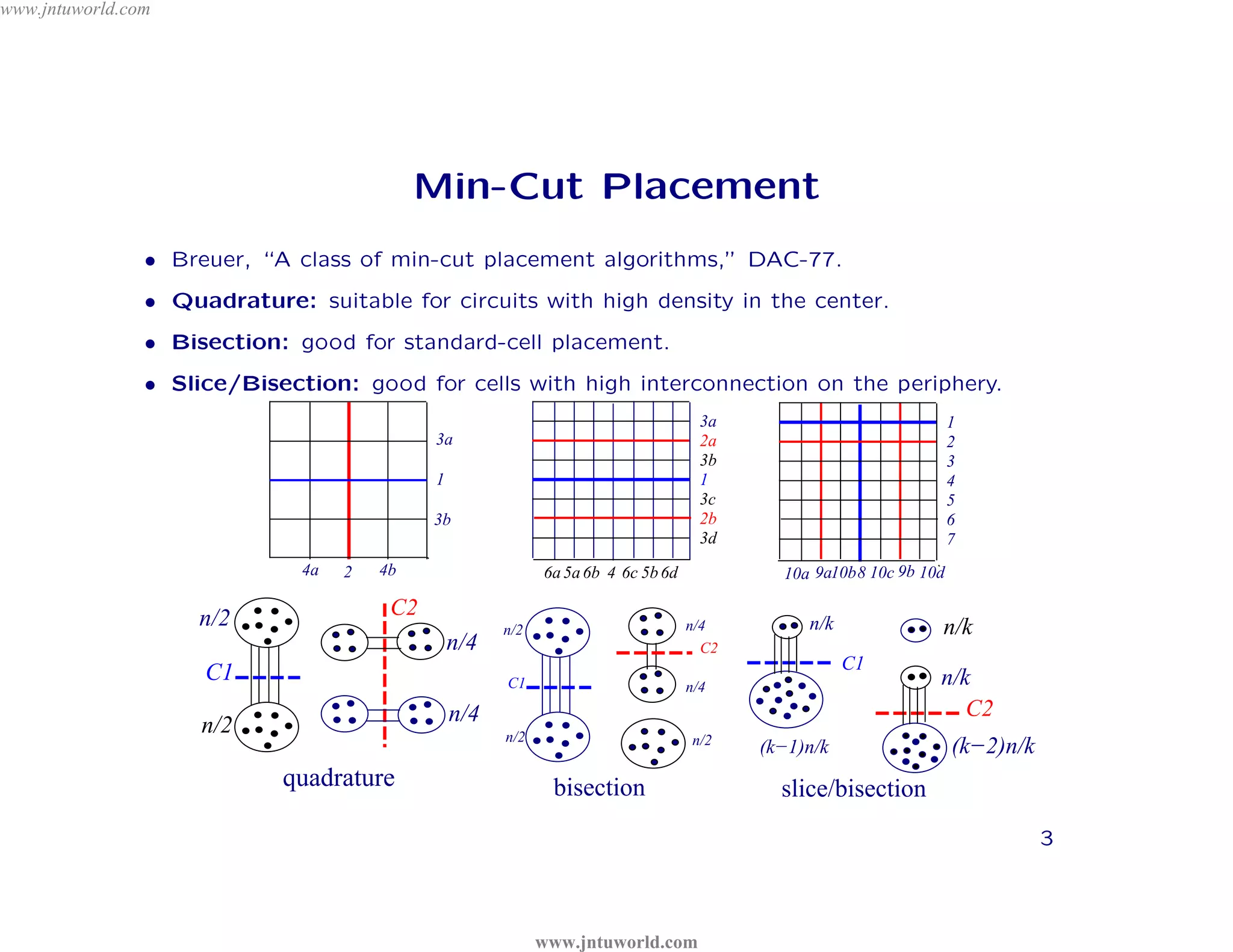
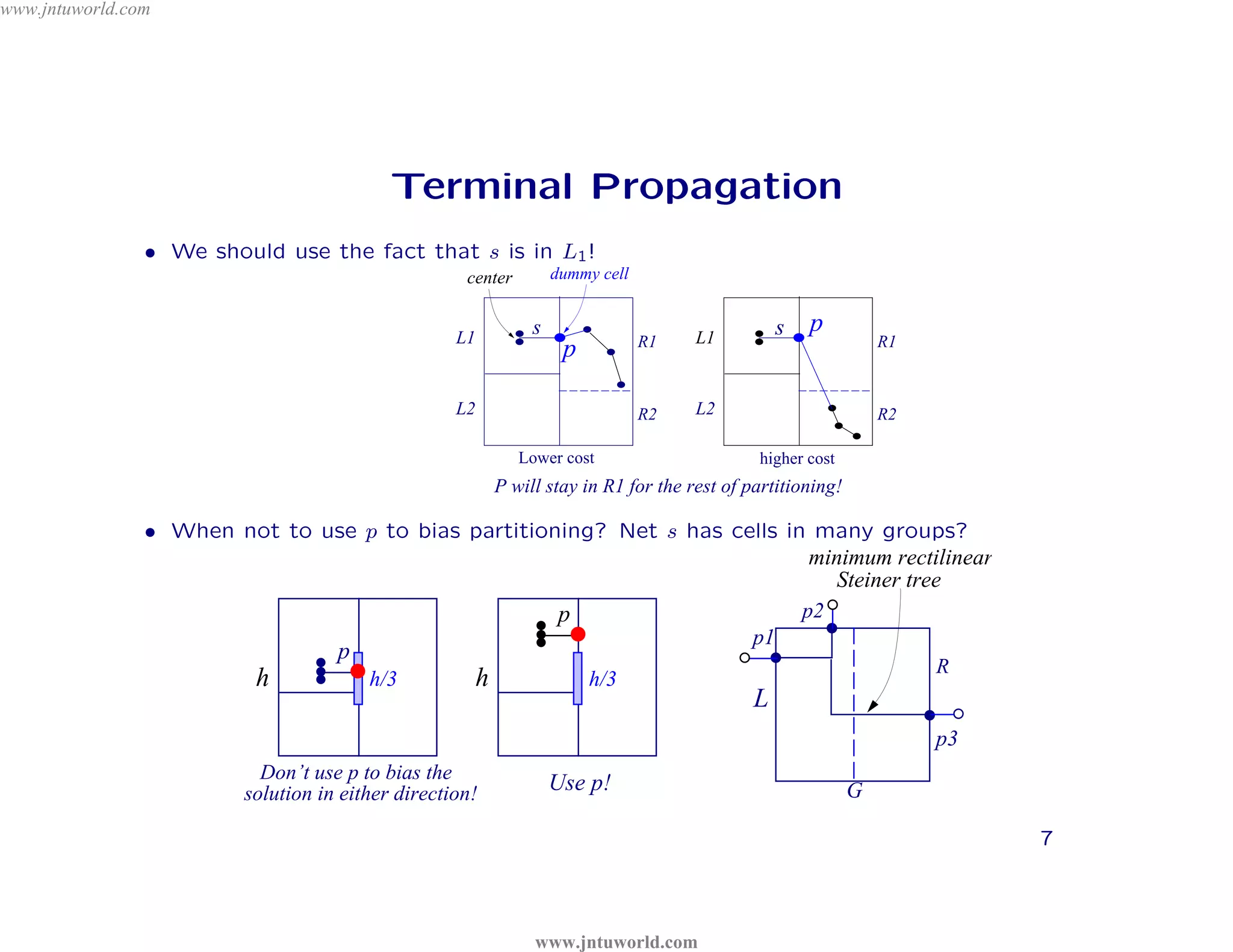
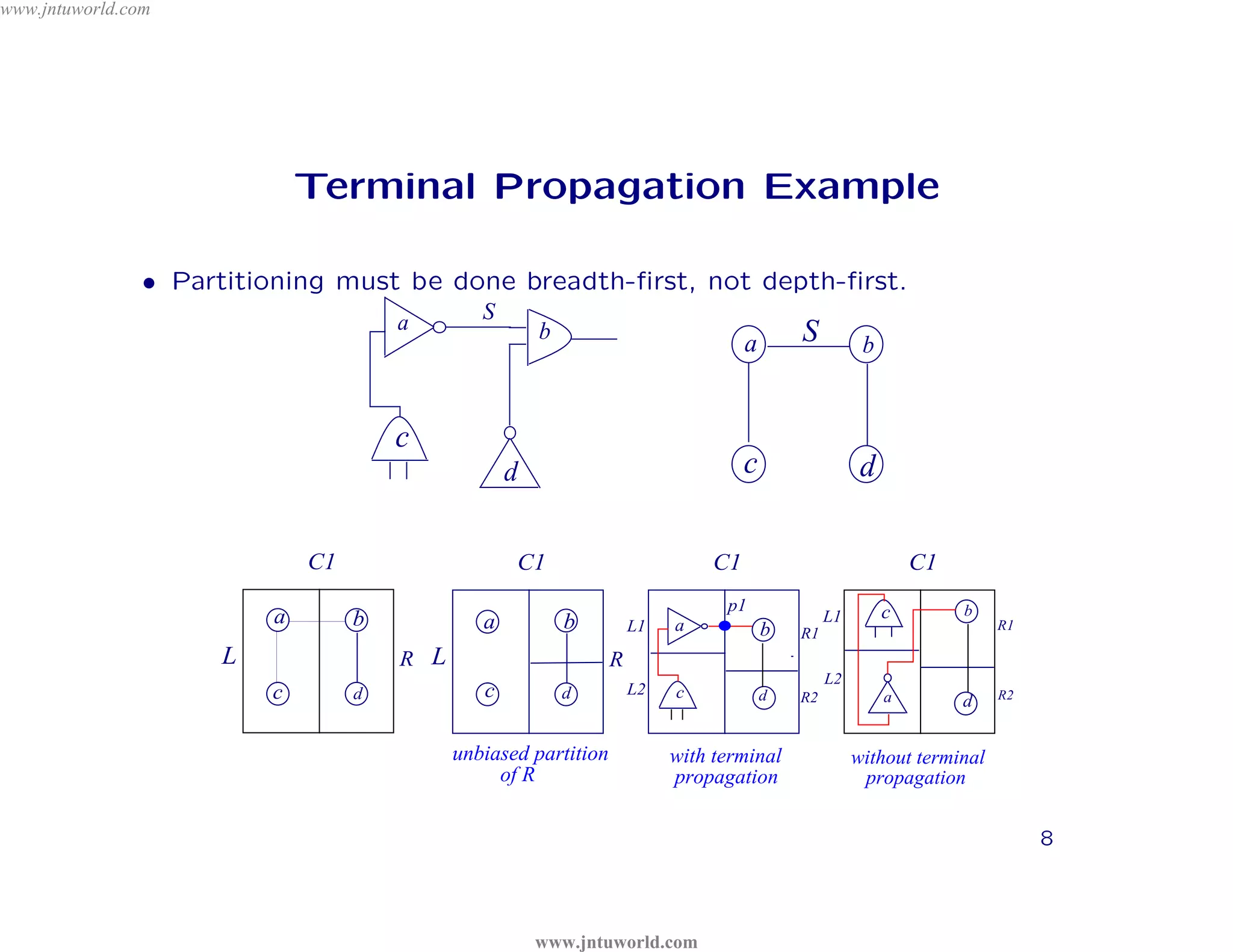
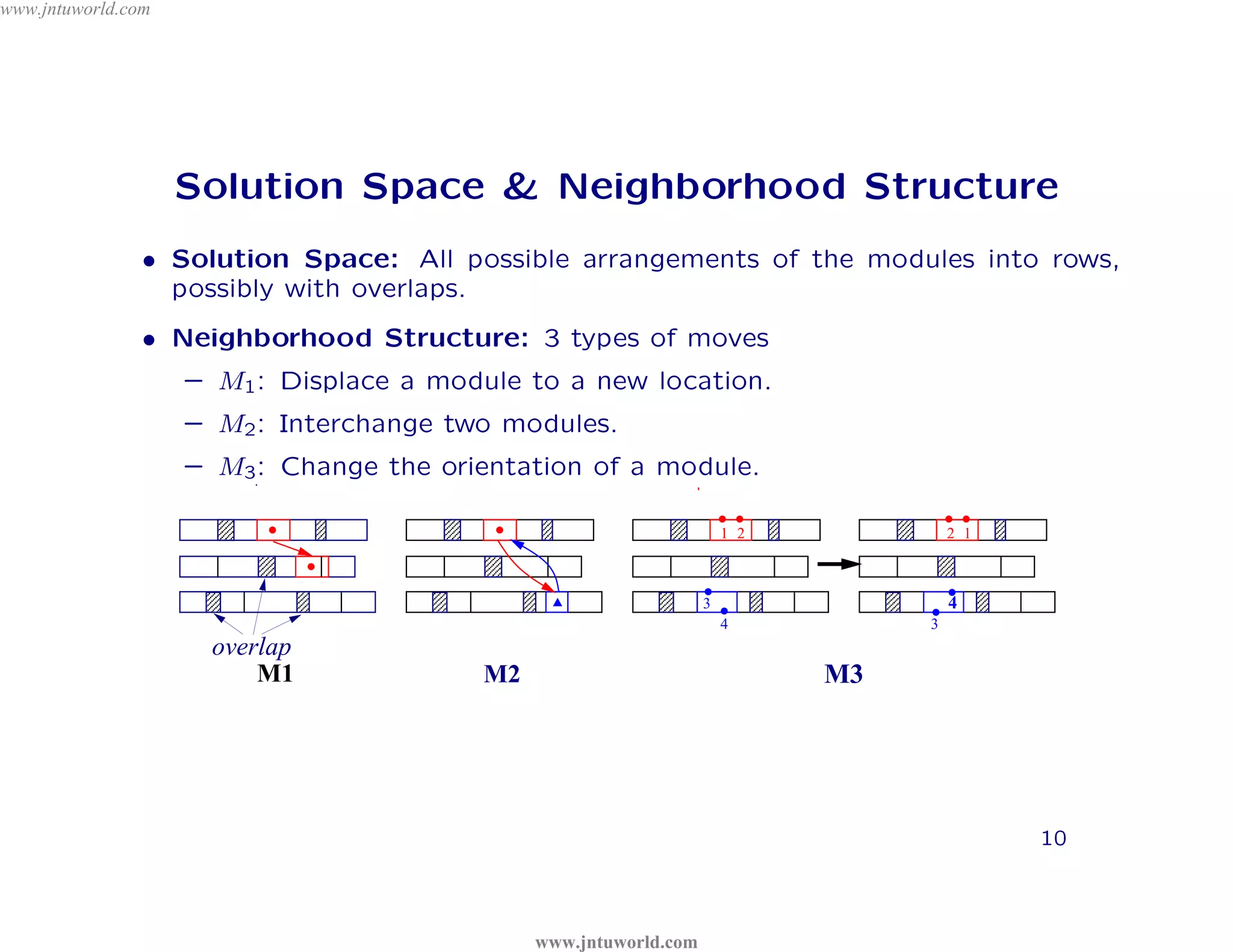
The document discusses placement algorithms used in circuit design. It describes the min-cut placement algorithm which partitions the layout surface and circuit into halves recursively to minimize wirelength. Terminal propagation is discussed to address limitations of min-cut by considering terminal pin positions. Placement by simulated annealing is also summarized, using neighborhood structures and cost functions to iteratively improve placement quality as temperature decreases.

1. www.jntuworld.com
Placement
D
• The process of arranging the circuit components on a layout surface.
L
• Inputs: A set of fixed modules, a netlist.
o m
R
. c
• Goal: Find the best position for each module on the chip according to
ld
O
appropriate cost functions.
or
– Considerations: routability/channel density, wirelength, cut size,
W
w
performance, thermal issues, I/O pads.
tu D B C A
U
jn
1 2 1 3
.
T
1
w
E F G H
5 5 6
3 5
w
2
N
Density = 2 (2 tracks required)
7 8
3
w 4 6 8 4
J
6 A B C D
4
8 7 2 7
E F G H
wirelength = 10 wirelength = 12
Shorter wirelength, 3 tracks required.
1
www.jntuworld.com

2. www.jntuworld.com
Estimation of Wirelength
D
• Semi-perimeter method: Half the perimeter of the bounding rectangle
L
approximation!
o m
that encloses all the pins of the net to be connected. Most widely used
R
.c
• Complete graph: Since #edges in a complete graph ( n(n−1) ) is n
ld
× #
O
2 2
or
2
of tree edges (n − 1), wirelength ≈ n (i,j)∈net dist(i, j).
W
tu
and then to the next closest, etc. w
• Minimum chain: Start from one vertex and connect to the closest one,
U
. jn
• Source-to-sink connection: Connect one pin to all other pins of the
T
net. Not accurate for uncongested chips.
w w
N
• Steiner-tree approximation: Computationally expensive.
w
J
• Minimum spanning tree
2
www.jntuworld.com

3. www.jntuworld.com
4
D
10 7
7 8 8
L
3 3
3
o m
R
. c 3
ld
4
O
or
semi−perimeter len = 11 complete graph len * 2/n = 17.5 chain len = 14
W
tu w
U
. jn
T
8
w
10
w 7
N
3 4 3
w
J
3
4
source−to−sink len = 17 Steiner tree len = 12 Spanning tree len = 13
www.jntuworld.com

4. www.jntuworld.com
Min-Cut Placement
D
• Breuer, “A class of min-cut placement algorithms,” DAC-77.
L
• Quadrature: suitable for circuits with high density in the center.
o m
R
• Bisection: good for standard-cell placement.
. c
ld
O
• Slice/Bisection: good for cells with high interconnection on the periphery.
or 3a 1
W
3a 2a 2
1
tu w 3b
1
3c
3
4
5
U
jn
3b 2b 6
.
3d 7
T
w
4a 2 4b 6a 5a 6b 4 6c 5b 6d 10a 9a10b8 10c 9b 10d
w
N
n/2 C2
n/2 n/4 n/k n/k
w n/4 C2
J
C1
C1 C1 n/4 n/k
n/4 C2
n/2 n/2 n/2
(k−1)n/k (k−2)n/k
quadrature bisection slice/bisection
3
www.jntuworld.com

5. www.jntuworld.com
Algorithm for Min-Cut Placement
D
Algorithm: Min Cut Placement(N, n, C)
L
/* N : the layout surface */
o m
R
/* n: # of cells to be placed */
/* n0 : # of cells in a slot */
. c
ld
O
/* C: the connectivity matrix */
or
W
1
2
begin
tu w
if (n ≤ n0 ) then PlaceCells(N, n, C);
U
jn
3 else
4
.
(N1 , N2 ) ← CutSurface(N );
T
5
w
6
w
(n1 , C1 ), (n2 , C2 ) ← Partition(n, C);
Call Min Cut Placement(N1 , n1 , C1 );
N
7 Call Min Cut Placement(N2 , n2 , C2 );
w end
J
8
4
www.jntuworld.com

6. www.jntuworld.com
Quadrature Placement Example
D
• Apply K-L heuristic to partition + Quadrature Placement: Cost C1 = 4, C2L = C2R = 2,
etc.
L
P
Q
2 4
7
8
o m
R
c
1 14 Q1
5 12
ld .
O
R
or
3
9 13
W
6
w
16 Q2
tu
11
U
n 10 15 Q3
.j
T
w w P 2 4 8 14 O1
N
C4a C4a
w 2,4,5,7 8,12,13,14 5 7 12 13
J
C2 C2 C2
1,3,6,9 10,11,15,16 Q 1 9 11 16 O2
C4b C4b
3 6 10 15 O3
C1 R
C3a C1 C3b
5
www.jntuworld.com

7. www.jntuworld.com
Min-Cut Placement with Terminal Propagation
D
• Dunlop & Kernighan, “A procedure for placement of standard-cell VLSI
L
circuits,” IEEE TCAD, Jan. 1985.
o m
R
. c
• Drawback of the original min-cut placement: Does not consider the
ld
O
positions of terminal pins that enter a region.
or
– What happens if we swap {1, 3, 6, 9} and {2, 4, 5, 7} in the previous
W
example?
tu w prefer to have them in R1
U
S
. jn S
T
L1
w w L1 R1
N
w R
J
L2 L2 R2
6
www.jntuworld.com

8. www.jntuworld.com
Terminal Propagation
D
• We should use the fact that s is in L1 !
center dummy cell
L
s s p
o m
R
L1
p R1 L1
. c R1
ld
O
or
L2 R2 L2 R2
W
Lower cost
tu w higher cost
P will stay in R1 for the rest of partitioning!
U
. jn
• When not to use p to bias partitioning? Net s has cells in many groups?
minimum rectilinear
T
w w Steiner tree
N
p p2
w
p1
p
J
R
h h/3 h h/3
L
p3
Don’t use p to bias the
solution in either direction! Use p! G
7
www.jntuworld.com

9. www.jntuworld.com
Terminal Propagation Example
D
• Partitioning must be done breadth-first, not depth-first.
L
a S
o m
R
b S
a
. c b
ld
O
c
or
W
d
tu w c d
U
. jn
T
C1 C1 C1 C1
w w
N
p1 c b
a b a b L1 a
L1 R1
b R1
L
w R L R
J
L2
c d c d L2 c d R2 a d R2
unbiased partition with terminal without terminal
of R propagation propagation
8
www.jntuworld.com

10. www.jntuworld.com
Placement by Simulated Annealing
D
• Sechen and Sangiovanni-Vincentelli, “The TimberWolf placement and
L
o m
routing package,” IEEE J. Solid-State Circuits, Feb. 1985; “TimberWolf
3.2: A new standard cell placement and global routing package,” DAC-
R
86.
.c
ld
O
or
• TimberWolf: Stage 1
W
– Modules are moved between different rows as well as within the same
row.
tu w
U
jn
– Modules overlaps are allowed.
.
– When the temperature is reached below a certain value, stage 2
T
begins.
w w
N
• TimberWolf: Stage 2
w
J
– Remove overlaps.
– Annealing process continues, but only interchanges adjacent modules
within the same row.
9
www.jntuworld.com

11. www.jntuworld.com
Solution Space & Neighborhood Structure
D
• Solution Space: All possible arrangements of the modules into rows,
L
possibly with overlaps.
o m
R
• Neighborhood Structure: 3 types of moves
.c
ld
O
– M1 : Displace a module to a new location.
– M2 : Interchange two modules.
or
W
w
– M3 : Change the orientation of a module.
tu
U
. jn 1 2 2 1
T
w w 3 4
N
4 3
overlap
w
J
M1 M2 M3
10
www.jntuworld.com

12. www.jntuworld.com
Neighborhood Structure
D
• TimberWolf first tries to select a move between M1 and M2 : P rob(M1 ) = 0.8, P rob(M2 ) =
0.2.
L
module will be chosen with probability 0.1.
o m
• If a move of type M1 is chosen and it is rejected, then a move of type M3 for the same
R
.c
• Restrictions: (1) what row for a module can be displaced? (2) what pairs of modules
ld
O
can be interchanged?
• Key: Range Limiter
or
W
tu w
– At the beginning, (WT , HT ) is very large, big enough to contain the whole chip.
– Window size shrinks slowly as the temperature decreases. Height and width ∝
U
jn
log(T ).
.
– Stage 2 begins when window size is so small that no inter-row module interchanges
T
are possible.
w w
N
w W
J
T
H
T
11
www.jntuworld.com

13. www.jntuworld.com
Cost Function
D
• Cost function: C = C1 + C2 + C3.
L
• C1 : total estimated wirelength.
o m
R
c
– C1 = (αi wi + βi hi )
.
i∈N ets
ld
– αi , βi are horizontal and vertical weights, respectively. (αi = 1, βi = 1 ⇒ 1 × perime-
O
2
or
ter of the bounding box of Net i.)
W
– Critical nets: Increase both αi and βi .
βi < αi .
tu w
– If vertical wirings are “cheaper” than horizontal wirings, use smaller vertical weights:
U
. jn
• C2 : penalty function for module overlaps.
T
w
– C2 = γ 2
Oij , γ: penalty weight.
i=j
w
N
– Oij : amount of overlaps in the x-dimension between modules i and j.
w
• C3 : penalty function that controls the row length.
J
– C2 = δ r∈Rows
|Lr − Dr |, δ: penalty weight.
– Dr : desired row length.
– Lr : sum of the widths of the modules in row r.
12
www.jntuworld.com

14. www.jntuworld.com
Annealing Schedule
D
• Tk = rk Tk−1 , k = 1, 2, 3, . . .
L
m
• rk increases from 0.8 to max value 0.94 and then decreases to 0.8.
o
R
• At each temperature, a total # of nP attempts is made.
.c n: # of
ld
O
modules; P : user specified constant.
• Termination: T < 0.1.
or
W
tu w
U
. jn
T
w w
N
w
J 13
www.jntuworld.com