Downloaded 183 times
Uploaded byMarina Santini
Lecture 9 Perceptron
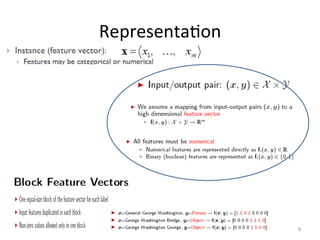
This document discusses the perceptron algorithm for linear classification. It begins by introducing feature representations and linear classifiers. It then describes the perceptron algorithm, which attempts to learn a weight vector that separates the training data into classes with some margin. The document proves that for any separable training set, the perceptron will converge after a finite number of mistakes, where the number depends on the margin size and properties of the data. However, it notes that while the perceptron finds weights perfectly classifying the training data, these weights may not generalize well to new examples.
More Related Content
Lecture 9 Perceptron
- 1. Machine Learning for Language Technology Lecture 9: Perceptron Marina San2ni Department of Linguis2cs and Philology Uppsala University, Uppsala, Sweden Autumn 2014 Acknowledgement: Thanks to Prof. Joakim Nivre for course design and materials 1
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8. Representa2on Linear Classifiers: Repe22on & Extension 8
- 15. Linear classifiers (atomic classes) Linear Classifiers: Repe22on & Extension 15 • Assump2on: data must be linearily separable
- 16.
- 17.
- 18.
- 19.
- 20. Separability and Margin (ii) Linear Classifiers: Repe22on & Extension 20 • Given a training instance, let Y bar t be the set of all labels that are incorrect, let’s define the set of incorrect labels minus the correct labels for that instance. • Then we say that a training set is separable with a margin gamma, if there exists a weight vector w that has a certain norm (ie 1), The score that we get when we use this vector w minus the score of every incorrect label is at least gamma
- 21. Separability and Margin (iii) • IMPORTANT: for every training instance the score that we get when we use the training vector w minus the score of every incorrect label is at least a certain margin gamma (ɣ). That is, the margin ɣ is the smallest difference between the score of the right class and the best score of the incorrect class. The higher the weights, the greater the norms. And we want this to be 1 (normalization). There are different ways of measuring the length/ magnitude of a vector and they are known as norms. The Eucledian norm (or L2 norm) says: take all the values of the weight vector, square them and sum them up, then take the square root .
- 22. Perceptron Linear Classifiers: Repe22on & Extension 22
- 23. Perceptron Learning Algorithm Linear Classifiers: Repe22on & Extension 23
- 24.
- 25. 25 Linear Classifiers: Repe22on & Extension Perceptron Theorem • For any training set that is separable with some margin, we can prove that the number of mistakes during training -‐-‐ if we keep itera2ng over the training set -‐-‐ is bounded by a quan2ty that depends on the size of the margin (see proofs in the Appendix, slides Lecture 3). • R depends on the norm of the largest difference you can have between feature vectors. The larger R, the more spread out the data, the more errors we can poten2ally make. Similarly if gamma is larger we will make fewer mistakes.
- 26.
- 27. Basically… 27 .... if it is possible to find such a weight vector for some posiAve margin gamma, then the training set is Linear Classifiers: Repe22on & Extension separable. So... if the training set is separable, Perceptron will eventually find the weight vector that separates the data. The 2me it takes depends on the property of the data. But aeer a finite number of itera2on, the training set will converge to 0. However... although we find the perfect weight vector for separa2ng the training data, it might be the case that the classifier has not good generaliza2on (do you remember the difference between empirical error and generaliza2on error?) So, with Perceptron, we have a fixed norm (=1) and variable margin (>0).
- 28. Appendix: Proofs and Deriva2ons