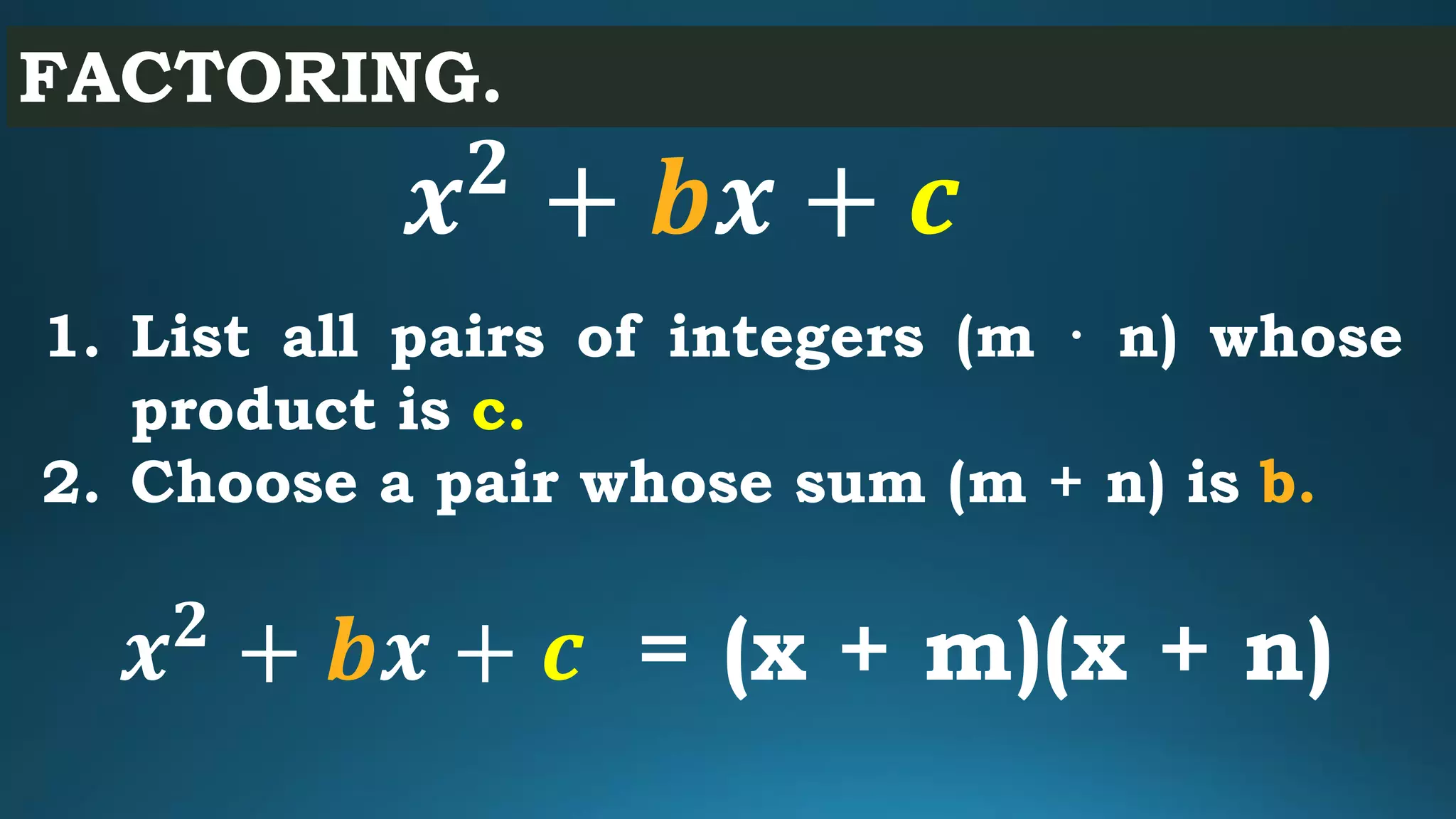This document focuses on factoring quadratic trinomials of the form x² + bx + c and solving related polynomial problems. It provides examples of factoring, listing integer pairs that relate to the coefficients, and offers practice problems involving factoring. The importance of identifying integer pairs that yield specific products and sums is emphasized throughout.

1. Grade 8 – Mathematics
Quarter I
FACTORING QUADRATIC TRINOMIALS
of the form 𝒙 𝟐
+ 𝒃𝒙 + 𝒄

2. Objectives:
1. factor quadratic trinomials of the
form 𝑥2
+ 𝑏𝑥 + 𝑐 ; and
2. solve problems involving factors
of polynomials.

3. List all pairs of integers (factors) of the
following numbers.
4
1 and 4
2 and 2
10
1 and 10
2 and 5
8
1 and 8
2 and 4
6
1 and 6
2 and 3

4. List all pairs of integers (factors) of the
following numbers.
12
1 and 12
2 and 6
3 and 4
30
1 and 30
2 and 15
3 and 10
20
1 and 20
2 and 10
4 and 5
18
1 and 18
2 and 9
3 and 6

5. FACTORING.
𝒙 𝟐
+ 𝒃𝒙 + 𝒄
1. List all pairs of integers (m · n) whose
product is c.
2. Choose a pair whose sum (m + n) is b.
𝒙 𝟐
+ 𝒃𝒙 + 𝒄 = (x + m)(x + n)

6. FACTORING.
𝒙 𝟐
+ 𝒃𝒙 + 𝒄
𝒙 𝟐
+ 𝒃𝒙 + 𝒄 = (x + m)(x + n)
(m · n)(m + n)
Factored Form

7. Example: 𝒙 𝟐
+ 𝟏𝟎𝒙 + 𝟏𝟔
List all pairs of integers whose product is c.
1 and 16 2 and 8 4 and 4
Choose a pair whose sum is b.
2 and 8 = 10
Factor as (x + m)(x + n).
m n
𝒙 𝟐
+ 𝟏𝟎𝒙 + 𝟏𝟔 = (x + 2)(x + 8)
(+)(+)
(-)(-)

8. Example: 𝒙 𝟐
− 𝟗𝒙 + 𝟏𝟖
List all pairs of integers whose product is c.
-1 and -18 -2 and -9 -3 and -6
Choose a pair whose sum is b.
-3 and -6 = -9
Factor as (x + m)(x + n).
m n
𝒙 𝟐
− 𝟗𝒙 + 𝟏𝟖 = (x - 3)(x - 6)
(+)(+)
(-)(-)

9. Example: 𝒙 𝟐
− 𝟐𝒙 − 𝟐𝟒
List all pairs of integers whose product is c.
1 and -24 2 and -12 4 and -6 3 and -8
Choose a pair whose sum is b.
4 and -6 = -2
Factor as (x + m)(x + n).
m n
𝒙 𝟐
− 𝟐𝒙 − 𝟐𝟒 = (x + 4)(x - 6)
(+) (-)larger
integer

10. Example: 𝒙 𝟐
+ 𝟑𝒙 − 𝟏𝟎
List all pairs of integers whose product is c.
-1 and 10 -2 and 5
Choose a pair whose sum is b.
-2 and 5 = 3
Factor as (x + m)(x + n).
m n
𝒙 𝟐
+ 𝟑𝒙 − 𝟏𝟎 = (x - 2)(x + 5)
(+) (-)larger
integer

11. Example: 𝒙 𝟐
+ 𝟑𝒙 + 𝟑
List all pairs of integers whose product is c.
1 and 3
since 1 and 3 = 4
PRIME TRINOMIAL
then 𝒙 𝟐
+ 𝟑𝒙 + 𝟑 cannot be factored
using integer coefficients, then it is…
(+)(+)
(-)(-)

12. Example:
Use factoring to find the dimensions of the
given box with volume represented by the
expression 𝟒𝒙 𝟑
+ 𝟏𝟔𝒙 𝟐
− 𝟒𝟖𝒙
The dimension of the box are
4x, x + 6 and x – 2
𝟒𝒙(𝒙 𝟐
+ 𝟒𝒙 − 𝟏𝟐)Factor out 4x.
4x(x + 6)(x – 2)Factor (𝒙 𝟐
+𝟒𝒙 − 𝟏𝟐)

13. Summary.
𝒙 𝟐
+ 𝟕𝒙 + 𝟏𝟎 (+)(+) or (-)(-)
𝒙 𝟐
− 𝟕𝒙 + 𝟏𝟎 (+)(+) or (-)(-)
𝒙 𝟐
+ 𝟑𝒙 − 𝟏𝟎 (+) (-)
𝒙 𝟐
− 𝟑𝒙 − 𝟏𝟎
larger integer
(+) (-)
larger integer