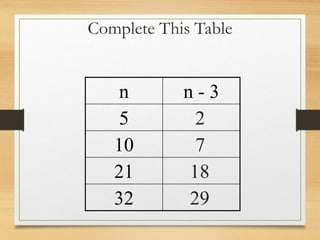
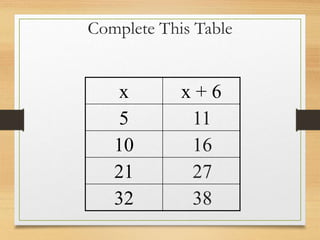
1) The document defines key algebraic terms like variables, constants, coefficients, terms, expressions, monomials, binomials, and trinomials. 2) It provides examples of writing algebraic expressions for word phrases and evaluating expressions for given values. 3) Tables are completed by applying operations like subtraction and addition to variables and values.

1. Algebraic
Expressions
CLASS VII

2. Definitions
• Variable – A variable is a letter
or symbol that represents a
number (unknown quantity).
• 2x + 5y
• 8 + n = 12

3. Definitions
• A variable can use any letter of the
alphabet.
• n + 5
• x – 7
• w - 25

4. Definitions
• A constant is a number that does not
change.
• A coefficient is a number multiplied or
divided by a variable.
6x + 5
6 is the coefficient, x is the variable, and 5 is the
constant.

5. Identify, in the following expressions, terms which are not
constants. Give their numerical coefficients:
xy + 4, 13 – y2 , 13 – y + 5y2 , 4p2 q – 3pq2 + 5

6. Definitions
•Algebraic expression – an
expression that contains at least one
variable, operation, and constant
•m + 8
•r – 3

7. Definitions
• A term is a part of an expression that
are added or subtracted
5x + 6 – 4x
This expression has 3 terms: 5x, 6, and
4x

8. TERMS ARE ADDED TO
FORM EXPRESSIONS
• Just as the terms 4x and 5 are added to
form the expression (4x + 5),
• The terms 4x2 and (–3xy) are added to
give the expression (4x2 – 3xy).
• This is because 4x2 + (–3xy) = 4x2– 3xy.

9. FACTORS OF A TERM
• The tree for the expression (4x2 – 3xy) is

10. • Let us draw a tree diagram for the expression
5xy + 10.

11. LIKE AND UNLIKE TERMS
• Like term are terms who have the same variable
raised to the same power ie. They have the same
algebraic factors.
• Unlike terms are terms who have the different
variable raised to the same or different power ie.
They do not have the same algebraic factors

12. State with reasons, which of the following pairs
of terms are of like terms and which are of
unlike terms: (i) 7x, 12y (ii) 15x, –21x (iii) – 4ab,
7ba (iv) 6xy2, 9x2y

13. Following simple steps will help you to decide whether the
given terms are like or unlike terms:
(i) Ignore the numerical coefficients. Concentrate on the
algebraic part of the terms.
(ii) Check the variables in the terms. They must be the
same.
(iii) Next, check the powers of each variable in the terms.
They must be the same.
Note that in deciding like terms, two things do not matter
(1) the numerical coefficients of the terms and
(2) the order in which the variables are multiplied in the
terms.

14. MONOMIALS,
BINOMIALS, TRINOMIALS
• An expression with only one term is called a
monomial; for example, 7xy, – 5m, 4, 3z2, etc.
• An expression which contains two unlike terms is
called a binomial; for example, x + y, m – 5,
mn+4m, a2– b2 are binomials.
• An expression which contains three terms is called a
trinomial; for example, the expressions x + y + 7,
ab+a+b, 3x2– 5x + 2, m + n + 10 are trinomials.

15. POLYNOMIALS
• In general, an expression with one or more terms is called a
polynomial. Thus a monomial, a binomial and a trinomial are all
polynomials.
• NOTE: The expression 10pq is not a binomial; it is a
monomial.
• The expression (a + b + 5) is not a binomial.It contains three
terms.
• The expression ab + a + b + 5 is not a trinomial; it contains
four terms and not three
• The expression x + y + 5x is not a trinomial as the terms x and
5x are like terms.

16. Words That Lead to Addition
• Sum
• More than
• Increased
• Plus
• Altogether

17. Words That Lead to Subtraction
• Decreased
• Less
• Difference
• Minus
• How many more

18. Write Algebraic Expressions
for These Word Phrases
• Ten more than a number
• A number decrease by 5
• 6 less than a number
• A number increased by 8
• The sum of a number & 9
• 4 more than a number
n + 10
w - 5
x - 6
n + 8
n + 9
y + 4

19. Write Algebraic Expressions
for These Word Phrases
• A number s plus 2
• A number decrease by 1
• 31 less than a number
• A number b increased by 7
• The sum of a number & 6
• 9 more than a number
s + 2
k - 1
x - 31
b + 7
n + 6
z + 9

20. Evaluate each algebraic expression
when x = 10
• x + 8
• x + 49
• x + x
• x - x
• x - 7
• 42 - x
18
59
20
0
3
32

21. Complete This Table
n n - 3
5
10
21
32
2
7
18
29

22. Complete This Table
x x + 6
5
10
21
32
11
16
27
38

23. Write an Algebraic Expression for
These Situations
• Suraj brother is 2 years younger than him
• The sum of two numbers is 12
• The difference between two numbers is 5
s - 2
x + y = 12
m – n = 5