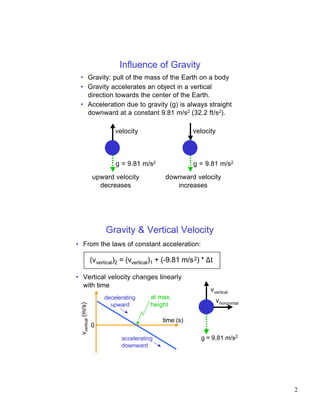
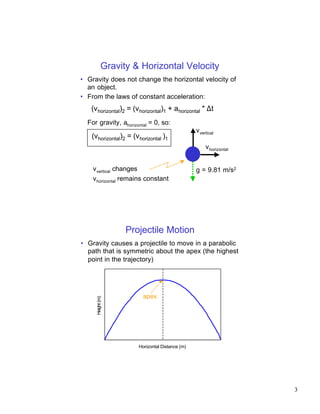
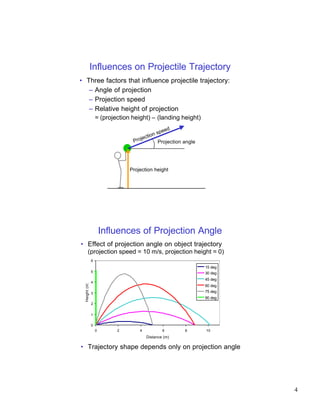
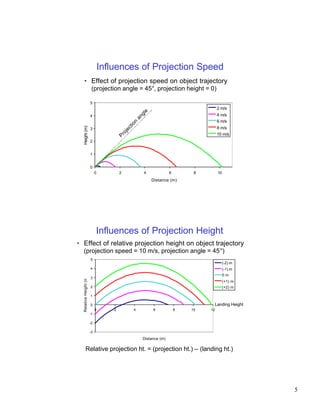
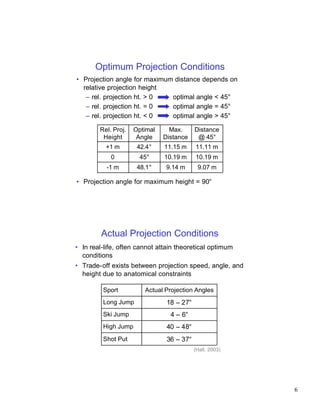
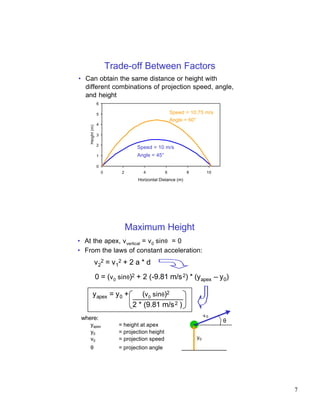
The document discusses projectile motion, which describes the trajectory of objects in free fall under only the forces of gravity and air resistance. It defines a projectile and explains how gravity influences the vertical and horizontal components of motion differently. Key factors that determine a projectile's trajectory include the projection angle, speed, and height. Optimal projection conditions exist that maximize distance or height based on these factors. Examples are provided to demonstrate how to calculate values like maximum height, flight time, and distance for a given projectile scenario.

1. Projectile Motion
Objectives:
• Understand projectile motion and how gravity
influences it
• Understand the effects of projection speed,
angle, and relative height on projectile motion
• Learn to compute the maximum height, flight
time, and flight distance of a projectile
What is a Projectile?
• A projectile is a body or object that
– is in the air
– is subject only to the forces of gravity and air
resistance
(i.e. the object is in free fall).
• The motion of the center of mass of any object in
free fall is governed by the laws of projectile motion
1

2. Influence of Gravity
• Gravity: pull of the mass of the Earth on a body
• Gravity accelerates an object in a vertical
direction towards the center of the Earth.
• Acceleration due to gravity (g) is always straight
downward at a constant 9.81 m/s2 (32.2 ft/s2).
velocity velocity
g = 9.81 m/s2 g = 9.81 m/s2
upward velocity downward velocity
decreases increases
Gravity & Vertical Velocity
• From the laws of constant acceleration:
(vvertical)2 = (vvertical)1 + (-9.81 m/s 2) * ∆t
• Vertical velocity changes linearly
with time
vvertical
decelerating at max.
vhorizontal
height
vvertical (m/s)
upward
time (s)
0
accelerating g = 9.81 m/s2
downward
2

3. Gravity & Horizontal Velocity
• Gravity does not change the horizontal velocity of
an object.
• From the laws of constant acceleration:
(vhorizontal)2 = (vhorizontal)1 + ahorizontal * ∆t
For gravity, ahorizontal = 0, so:
vvertical
(vhorizontal)2 = (vhorizontal )1
vhorizontal
vvertical changes g = 9.81 m/s2
vhorizontal remains constant
Projectile Motion
• Gravity causes a projectile to move in a parabolic
path that is symmetric about the apex (the highest
point in the trajectory)
apex
Height (m)
Horizontal Distance (m)
3

4. Influences on Projectile Trajectory
• Three factors that influence projectile trajectory:
– Angle of projection
– Projection speed
– Relative height of projection
= (projection height) – (landing height)
ed
spe
ion
ject
Pro Projection angle
Projection height
Influences of Projection Angle
• Effect of projection angle on object trajectory
(projection speed = 10 m/s, projection height = 0)
6
15 deg
5 30 deg
45 deg
4
Height (m)
60 deg
3 75 deg
90 deg
2
1
0
0 2 4 6 8 10
Distance (m)
• Trajectory shape depends only on projection angle
4

5. Influences of Projection Speed
• Effect of projection speed on object trajectory
(projection angle = 45°, projection height = 0)
5
2 m/s
e
gl
4 4 m/s
an
6 m/s
n
tio
Height (m)
3
ec 8 m/s
oj
10 m/s
Pr
2
1
0
0 2 4 6 8 10
Distance (m)
Influences of Projection Height
• Effect of relative projection height on object trajectory
(projection speed = 10 m/s, projection angle = 45°)
5
(-2) m
4 (-1) m
0m
Relative Height (m)
3
(+1) m
2 (+2) m
1
0 Landing Height
0 2 4 6 8 10 12
-1
-2
-3
Distance (m)
Relative projection ht. = (projection ht.) – (landing ht.)
5

6. Optimum Projection Conditions
• Projection angle for maximum distance depends on
relative projection height
– rel. projection ht. > 0 optimal angle < 45°
– rel. projection ht. = 0 optimal angle = 45°
– rel. projection ht. < 0 optimal angle > 45°
Rel. Proj. Optimal Max. Distance
Height Angle Distance @ 45°
+1 m 42.4° 11.15 m 11.11 m
0 45° 10.19 m 10.19 m
-1 m 48.1° 9.14 m 9.07 m
• Projection angle for maximum height = 90°
Actual Projection Conditions
• In real-life, often cannot attain theoretical optimum
conditions
• Trade-off exists between projection speed, angle, and
height due to anatomical constraints
Sport Actual Projection Angles
Long Jump 18 – 27°
Ski Jump 4 – 6°
High Jump 40 – 48°
Shot Put 36 – 37°
(Hall, 2003)
6

7. Trade-off Between Factors
• Can obtain the same distance or height with
different combinations of projection speed, angle,
and height
6
5 Speed = 10.75 m/s
Angle = 60°
4
Height (m)
3
2
Speed = 10 m/s
1 Angle = 45°
0
0 2 4 6 8 10
Horizontal Distance (m)
Maximum Height
• At the apex, vvertical = v0 sinθ = 0
• From the laws of constant acceleration:
v22 = v 12 + 2 a * d
0 = (v0 sinθ)2 + 2 (-9.81 m/s 2) * (yapex – y0)
yapex = y 0 + (v0 sinθ)2
2 * (9.81 m/s 2 )
where: v0
θ
yapex = height at apex
y0 = projection height
v0 = projection speed y0
θ = projection angle
7

8. Example Problem #1
A high jumper leave the ground with a velocity of
6 m/s at a projection angle of 40°. Her center
of mass is 1 m above the ground at take-off.
What is the maximum height of her center of
mass during the jump?
Flight Time
• From the laws of constant acceleration:
d = v 1 * ∆ t + (½) a * ( ∆ t)2
(yfinal – y0) = (v0 sinθ) * tF + (½)*(-9.81 m/s 2)* tF2
Solve the above quadratic equation to find the flight
time tF (choose the largest positive answer)
where:
v0
yfinal = final height θ
y0 = projection height
v0 = projection speed
y0 y final
θ = projection angle
8

9. Example Problem #2
A figure skater is attempting a jump in which she
performs 3 complete revolutions while in the air.
She leaves the ice with a velocity of 7 m/s at a
projection angle of 30°
If she spins at 3 revolutions per second, will she be
able to complete all 3 revolutions before landing?
Flight Distance
• During projectile motion, vhorizontal = v0 cos θ is constant
• From the laws of constant acceleration with a = 0:
d = v1 * ∆t
dF = (v 0 cos θ) * tF
where:
dF = flight distance v0
θ
tF = flight time
v0 = projection speed
θ = projection angle
dF
9

10. Example Problem #3
A kicker is attempting field goal from 40 yards away.
The ball is kicked with an initial velocity of 24 m/s at
a projection angle of 30°.
The crossbar of the goal post is 10 ft above the
ground.
If his aim is correct, will he make the field goal?
Effects on Projectile Motion
Variable Determined by:
Projection speed
Horizontal velocity
Projection angle
Projection speed
Vertical velocity
Projection angle
Vertical velocity
Maximum height
Projection height
Vertical velocity
Flight time Projection height
Final height
Horizontal velocity
Flight distance
Flight time
10

11. Influence of Air Resistance
• In real-life, air resistance will cause both horizontal
and velocity to change while in flight.
• Forces created by wind will also affect the trajectory
No Air Resist
Air Resist
Tailwind
Height (m)
Oblique
Trajectory
Horizontal Distance (m)
11