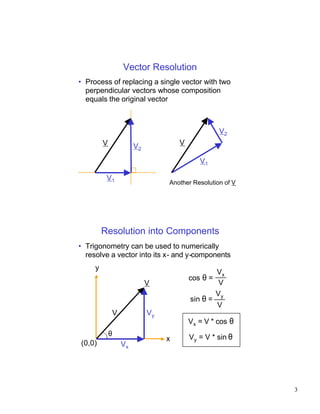
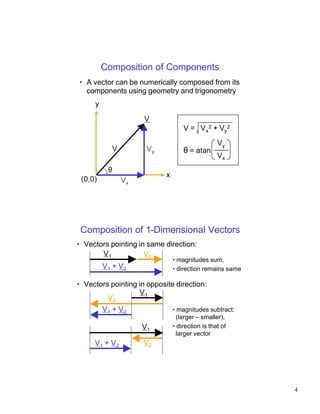
The document defines vectors and describes various vector operations that can be performed, including: - Graphical vector addition using the tip-to-tail method - Numerical representation of vectors using magnitude, direction, and components - Resolution of a vector into perpendicular components - Composition and decomposition of vectors using graphical and numerical methods - Scalar multiplication and subtraction of vectors It also provides examples of how to use vectors to solve problems graphically or numerically.

1. Vectors
Objectives:
• Define the concept of a vector
• Learn how to perform basic vector
operations using graphical and
numerical methods
• Learn how to use vector algebra to
solve simple problems
Vector
A vector is a quantity that has:
• a magnitude
• a direction
(e.g. change in position)
V
A scalar quantity has magnitude only (e.g. time)
1

2. Numerical Representation
Methods of expressing a vector (V) numerically:
• its magnitude (V) and direction (θ) with respect
to a reference axis
• its components (Vx, Vy) along each reference
axis
y
Vy V
V
θ
x
(0,0) Vx
Vector Composition
• Process of determining a single vector from
two or more vectors by vector addition
• Performed graphically using tip-to-tail method
V1 + V2 copy of
V2 V2
V1
resultant : vector resulting from the composition
2

3. Vector Resolution
• Process of replacing a single vector with two
perpendicular vectors whose composition
equals the original vector
V2
V V2 V
V1
V1
Another Resolution of V
Resolution into Components
• Trigonometry can be used to numerically
resolve a vector into its x- and y-components
y
Vx
cos θ =
V V
Vy
sin θ =
V
V Vy
Vx = V * cos θ
θ Vy = V * sin θ
x
(0,0) Vx
3

4. Composition of Components
• A vector can be numerically composed from its
components using geometry and trigonometry
y
V
V = V x2 + Vy2
Vy
V Vy θ = atan
Vx
θ
x
(0,0) Vx
Composition of 1-Dimensional Vectors
• Vectors pointing in same direction:
V1 V2
• magnitudes sum,
V1 + V2 • direction remains same
• Vectors pointing in opposite direction:
V1
V2
V1 + V2 • magnitudes subtract:
(larger – smaller),
V1 • direction is that of
larger vector
V1 + V2 V2
4

5. Numerical Vector Composition
1. Draw x- and y-axes
2. Resolve each vector into x and y components
3. x component of resultant = add each
component pointing in +x direction and subtract
each component pointing in –x direction.
4. y component of resultant = add each
component pointing in +y direction and subtract
each component pointing in –y direction.
5. Draw the x and y components of the resultant
6. Compose the resultant from its components
Example VR
y V2
V2 VRy
V2y = V 2 sin θ2
V1
θR V1y = V 1 sin θ1
θ2 θ1
x
V2x = V 2 cos θ2 VRx V1x = V 1 cos θ1
VRx = V1x – V2x VR = VRx2 + VRy2
VRy = V1y + V2y θR = atan (VRy / VRx )
5

6. Alternate Method of Composition
1. Draw vectors “tip-to-tail”
2. Draw resultant vector to form a triangle
3. Draw x- and y-axes at tail of first vector
4. Determine the angle between the first and
second vector in the triangle.
5. Use Law of Cosines to determine the
magnitude of the resultant.
6. Use Law of Sines to determine the angle
between the first vector and the resultant
7. Compute direction of the resultant from
identified angles
Example
y V2
V2
VR
α sin α sin β
β =
VR V2
θR V1 V2 sin α
θ1 β = asin
x VR
VR = V 12 + V22 – 2V1V2 cos α
θR = θ1 + β
6

7. Vector-Scalar Multiplication
If a vector V is multiplied by a scalar n:
• If n > 0:
– magnitude of resultant = n * V
– direction of resultant = direction of V
• If n < 0:
– magnitude of resultant = (–n) * V
– direction of resultant = opposite direction of V
3*V
V
θ
θ
-1 * V
Vector Subtraction
• Subtraction of a vector performed by adding
(–1) times the vector
• Can be performed graphically or numerically
V2
V1 -1 * V2
-1 * V2 V1 – V2
7

8. Subtraction as a Change
• Subtraction can be pictured as the difference
or change between two vectors that originate
from the same point
y V1 + (V2 – V1) = V2
V1 V2 – V1
V2
x
Graphical Solution Using Vectors
1. Establish a scaling factor for the graph
(e.g. 1cm = 10 m/s)
2. Carefully draw vectors with the correct length
(based on the scaling factor) and direction
3. Use graphical methods of composition,
resolution, scalar multiplication, and/or
subtraction to find desired resultant
4. Carefully measure the length and direction of
the resultant.
5. Use scaling factor to convert measured length
to magnitude
8

9. Example Problem #1
Two volleyball players simultaneously contact the
ball above the net.
Player #1 hits the ball from the left with a force of
300 N (67 lb), angled 45° below the horizontal.
Player #2 hits the ball from the right with a force of
250 N (56 lb), angled 20° below the horizontal.
What is the magnitude and direction of the net
force applied to the ball by the 2 players?
Numerical Solutions Using Vectors
1. Sketch the vectors on a diagram of the
problem
2. Choose and diagram the coordinate axes,
based on:
• axes used in the problem statement
• axes that are physically meaningful
3. Establish and label known magnitudes and
angles or x- and y-components
4. Use numerical methods of composition,
resolution, scalar multiplication, and/or
subtraction to find desired solution
9

10. Graphical vs. Numerical Method
• Graphical Method
– Simple
– Must be done by hand
– Gives approximate result
• Numerical Method
– Requires complex calculations
– Gives accurate result
– Can be performed by computer
– Can perform analyses in 3 dimensions
Example Problem #2
A golfer is teeing off from the center of the
fairway for a hole that is located 300 yards
away and 30° to the right of center.
The golfer’s tee shot goes 210 yards and 15° to
the left of center of the fairway.
To reach the hole on the second shot, how far
and in what direction must the golfer hit the
ball?
10